【数学】2019届一轮复习人教A版　算法、复数、推理与证明学案

【数学】2019届一轮复习人教A版　算法、复数、推理与证明学案

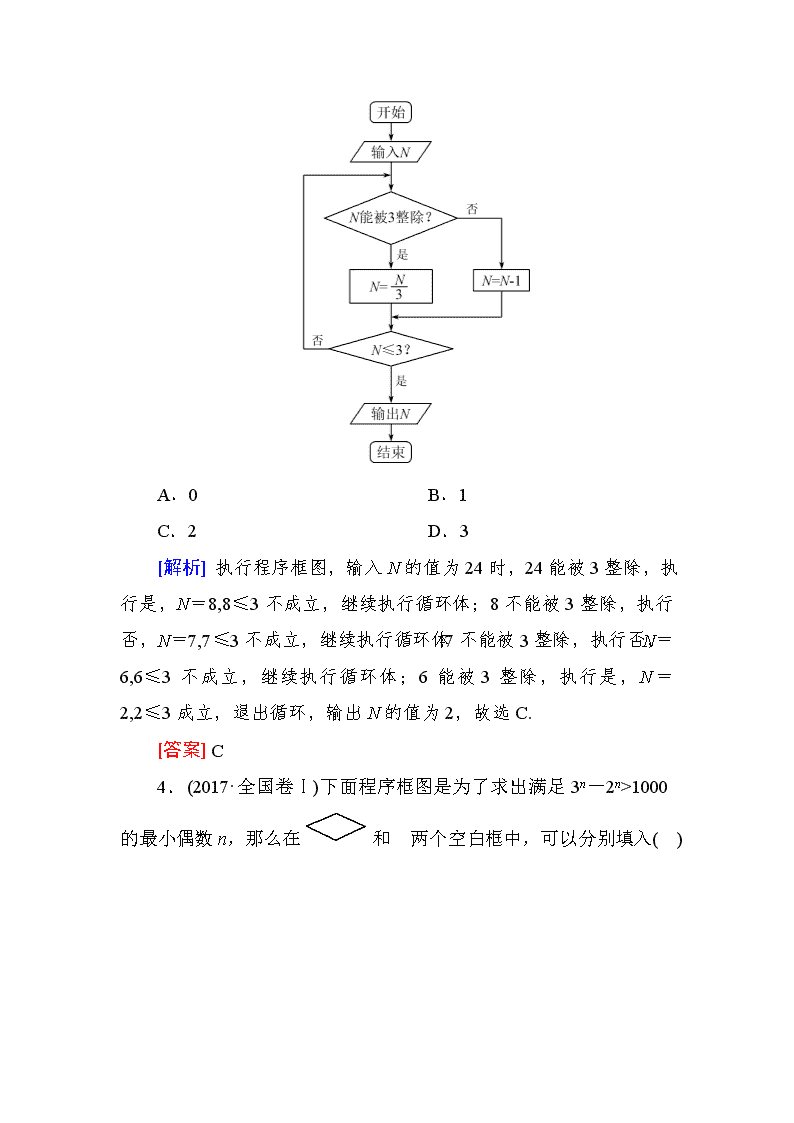
专题六 概率与统计、算法、复数、推理与证明 第四讲 算法、复数、推理与证明 高考导航 ‎1．对复数的考查主要是复数概念、复数四则运算和复数的几何意义．‎ ‎2．对程序框图的考查主要以循环结构的程序框图为载体考查学生对算法的理解．‎ ‎3．对合情推理的考查主要以归纳推理为主，考查学生的观察、归纳和概括能力.‎ ‎1．(2017·全国卷Ⅱ)＝( )‎ A．1＋2i B．1－2i C．2＋i D．2－i ‎[解析] ＝＝＝2－i.故选D.‎ ‎[答案] D ‎2．(2017·全国卷Ⅰ)设有下面四个命题：‎ p1：若复数 满足∈R，则 ∈R；‎ p2：若复数 满足 2∈R，则 ∈R；‎ p3：若复数 1， 2满足 1 2∈R，则 1＝2；‎ p4：若复数 ∈R，则∈R.‎ 其中的真命题为( )‎ A．p1，p3 B．p1，p4‎ C．p2，p3 D．p2，p4‎ ‎[解析] 对于命题p1，设 ＝a＋bi(a，b∈R)，由＝＝∈R，得b＝0，则 ∈R成立，故命题p1正确；对于命题p2，设 ＝a＋bi(a，b∈R)，由 2＝(a2－b2)＋2abi∈R，得a·b＝0，则a＝0或b＝0，复数 可能为实数或纯虚数，故命题p2错误；对于命题p3，设 1＝a＋bi(a，b∈R)， 2＝c＋di(c，d∈R)，由 1· 2＝(ac－bd)＋(ad＋bc)i∈R，得ad＋bc＝0，不一定有 1＝2，故命题p3错误；对于命题p4，设 ＝a＋bi(a，b∈R)，则由 ∈R，得b＝0，所以＝a∈R成立，故命题p4正确．故选B.‎ ‎[答案] B ‎3．(2017·天津卷)阅读下面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为( )‎ A．0 B．1 ‎ C．2 D．3‎ ‎[解析] 执行程序框图，输入N的值为24时，24能被3整除，执行是，N＝8,8≤3不成立，继续执行循环体；8不能被3整除，执行否，N＝7,7≤3不成立，继续执行循环体；7不能被3整除，执行否，N＝6,6≤3不成立，继续执行循环体；6能被3整除，执行是，N＝2,2≤3成立，退出循环，输出N的值为2，故选C.‎ ‎[答案] C ‎4．(2017·全国卷Ⅰ)下面程序框图是为了求出满足3n－2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入( )‎ A．A>1000？和n＝n＋1‎ B．A>1000？和n＝n＋2‎ C．A≤1000？和n＝n＋1‎ D．A≤1000？和n＝n＋2‎ ‎[解析] 本题求解的是满足3n－2n>1000的最小偶数n，可判断出循环结构为当型循环结构，即满足条件要执行循环体，不满足条件要输出结果，所以判断语句应为A≤1000？，另外，所求为满足不等式的偶数解，因此中语句应为n＝n＋2，故选D.‎ ‎[答案] D ‎5．(2017·北京卷)三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i＝1,2,3.‎ ‎(1)记Qi为第i名工人在第一天中加工的零件总数，则Q1，Q2，Q3中最大的是________；‎ ‎(2)记pi为第i名工人在这一天中平均每小时加工的零件数，则p1，‎ p2，p3中最大的是________．‎ ‎[解析] 设线段AiBi的中点为Ci(xi，yi)．‎ ‎(1)由题意知Qi＝2yi，i＝1,2,3，由题图知y1最大，所以Q1，Q2，Q3中最大的是Q1.‎ ‎(2)由题意知pi＝＝，i＝1,2,3.‎ 的几何意义为点Ci(xi，yi)与原点O连线的斜率．‎ 比较OC1，OC2，OC3的斜率，由题图可知OC2的斜率最大，即p2最大．‎ ‎[答案] (1)p1 (2)p2‎ 考点一 复数的概念与运算 ‎1．复数的除法 复数的除法一般是先将分母实数化，即分子、分母同乘以分母的共轭复数再进一步化简．‎ ‎2．复数运算中常见的结论 ‎(1)(1±i)2＝±2i，＝i，＝－i；‎ ‎(2)i4n＝1，i4n＋1＝i，i4n＋2＝－1，i4n＋3＝－i；‎ ‎(3)i4n＋i4n＋1＋i4n＋2＋i4n＋3＝0.‎ ‎[对点训练]‎ ‎1．(2017·全国卷Ⅲ)设复数 满足(1＋i) ＝2i，则| |＝( )‎ A. B. ‎ C. D．2‎ ‎[解析] 解法一：∵(1＋i) ＝2i，∴ ＝＝＝＝1＋i.‎ ‎∴| |＝＝.‎ 解法二：∵(1＋i) ＝2i，∴|1＋i|·| |＝|2i|，即·| |＝2，∴| |＝.‎ ‎[答案] C ‎2．(2017·北京卷)若复数(1－i)(a＋i)在复平面内对应的点在第二象限，则实数a的取值范围是( )‎ A．(－∞，1) B．(－∞，－1)‎ C．(1，＋∞) D．(－1，＋∞)‎ ‎[解析] ∵复数(1－i)(a＋i)＝a＋1＋(1－a)i在复平面内对应的点在第二象限，∴∴a<－1，故选B.‎ ‎[答案] B ‎3．(2017·山东卷)已知a∈R，i是虚数单位．若 ＝a＋i， ·＝4，则a＝( )‎ A．1或－1 B.或－ C．－ D. ‎[解析] ∵ ＝a＋i，∴＝a－i，又∵ ·＝4，∴(a＋i)(a－i)＝4，∴a2＋3＝4，∴a2＝1，∴a＝±1.故选A.‎ ‎[答案] A ‎4．(2017·西安模拟)若 ＝(a－)＋ai为纯虚数，其中a∈R，则＝( )‎ A．i B．1 ‎ C．－i D．－1‎ ‎[解析] ∵ 为纯虚数，∴∴a＝，‎ ‎∴＝＝＝＝－i.‎ ‎[答案] C ‎ 复数问题的解题思路 以复数的基本概念、几何意义、相等的条件为基础，结合四则运算，利用复数的代数形式列方程或方程组解决问题．‎ 考点二 程序框图 ‎1．当需要对研究的对象进行逻辑判断时，要使用条件结构，它是根据指定条件选择执行不同指令的控制结构．‎ ‎2．注意直到型循环和当型循环的本质区别：直到型循环是先执行再判断，直到满足条件才结束循环；当型循环是先判断再执行，若满足条件，则进入循环体，否则结束循环．‎ ‎3．循环结构主要用在一些有规律的重复计算的算法中，如累加求和、累乘求积等．‎ ‎[对点训练]‎ ‎1．(2017·全国卷Ⅱ)执行下面的程序框图，如果输入的a＝－1，则输出的S＝( )‎ A．2 B．3 ‎ C．4 D．5‎ ‎[解析] 由程序框图可得S＝0，a＝－1，K＝1≤6；‎ S＝0＋(－1)×1＝－1，a＝1，K＝2≤6；‎ S＝－1＋1×2＝1，a＝－1，K＝3≤6；‎ S＝1＋(－1)×3＝－2，a＝1，K＝4≤6；‎ S＝－2＋1×4＝2，a＝－1，K＝5≤6；‎ S＝2＋(－1)×5＝－3，a＝1，K＝6≤6；‎ S＝－3＋1×6＝3，a＝－1，K＝7>6，退出循环，‎ 输出S＝3.故选B.‎ ‎[答案] B ‎2．(2017·西安八校联考)如图给出的是计算＋＋＋…＋＋的值的程序框图，其中判断框内应填入的是( )‎ A．i≤2014? B．i≤2016?‎ C．i≤2018? D．i≤2020?‎ ‎[解析] 依题意得，S＝0，i＝2；S＝0＋，i＝4；…；S＝0＋＋＋…＋＋，i＝2018，输出的S＝＋＋＋…＋＋，所以题中的判断框内应填入的是“i≤2016？”，选B.‎ ‎[答案] B ‎3．(2017·江西南昌三模)263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为( )‎ ‎(参考数据：≈1.732，sin15°≈0.2588，sin7.5°≈0.1305)‎ A．12 B．24 ‎ C．36 D．48‎ ‎[解析] 执行程序框图，可得n＝6，S＝3sin60°＝≈2.598，不满足条件S≥3.10，继续循环；‎ n＝12，S＝6×sin30°＝3，不满足条件S≥3.10，继续循环；‎ n＝24，S＝12×sin15°≈3.1056，满足条件S≥3.10，退出循环，输出n的值为24.故选B.‎ ‎[答案] B ‎ 求解程序框图2类常考问题的解题技巧 ‎(1)程序框图的运行结果问题 先要找出控制循环的变量及其初值、终值．然后看循环体，若循环次数较少，可依次列出即可得到答案；若循环次数较多，可先循环几次，找出规律．要特别注意最后输出的是什么，不要出现多一次或少一次循环的错误，尤其对于以累和为限定条件的问题，需要逐次求出每次迭代的结果，并逐次判断是否满足终止条件．‎ ‎(2)程序框图的填充问题 最常见的是要求补充循环结构的判断条件，解决此类问题的方法是创造参数的判断条件为“i>n？”或“i

查看更多