2018届二轮复习巧用抛物线的定义课件（全国通用）

2018届二轮复习巧用抛物线的定义课件（全国通用）

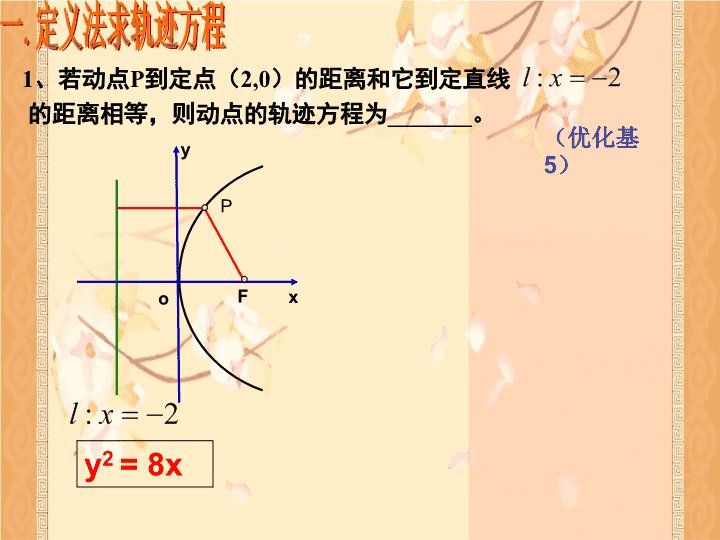
巧用抛物线的定义 类型二 利用定义法求值 类型三 利用定义法求最值 二、用定义法解题的常见类型 一、回顾抛物线的定义 类型一 利用定义法求轨迹 一 . 定义法求轨迹方程 1 、若动点 P 到定点（ 2,0 ）的距离和它到定直线 的距离相等，则动点的轨迹方程为 _______ 。 （优化基 5 ） P F o y x y 2 = 8x P F o x y y 2 = 8x 一 . 定义法求轨迹方程 变式 1 ：若动点 P 到定点（ 2,0 ）的距离比它到定直线 的距离小 1 ，则动点的轨迹方程为 _______ 。 y 2 = 8x 一 . 定义法求轨迹方程 变式 2 ： 若动圆与圆 C:( x -2) 2 + y 2 =1 外切，又与直线 相切，则动圆圆心的轨迹方程是 _______ 。 P F o x y 定位 用定义法求轨迹方程的一般步骤： 一 . 定义法求轨迹方程 文字特征 ： 数字特征 ： 结构特征 ： 如何定性： 位置关系特征 ： 定性 定方程 定量 定点、定直线 由定点的坐标和定直线的方程可以猜想到可能是焦点或准线； 定点在轴上，定直线与定点所在轴垂直； 两距离相等，或可通过平移直线的位置构造出距离相等。 1 ： 过抛物线 的焦点 F 作倾斜角为 60 0 的直线交抛物线于 A 、 B 两点，求 |AB| 的长度。 二 . 定义法求值 B A F x y O 二 . 定义法求值 点评： 过抛物线 的焦点 F 作倾斜角为 60 0 的直线交抛物线于 A 、 B 两点，求 |AB| 的长度。 过焦点弦 AB 长公式为 过抛物线 的焦点 F 作倾斜角为 60 0 的直线交抛物线于 A 、 B 两点，求 |AB| 的长度。 二 . 定义法求值 B A F x y O 二 . 定义法求值 2 、 点评： 二 . 定义法求值 涉及焦半径或者焦点弦通常都要用到 定义 ； 通常有 代数法 和 几何法 两种解题方向，几何法注重定义和平面几何性质的综合应用。 例 1-2 ： 在抛物线 y 2 =2x 上求一点 P ，使得点 P 到焦点的距离与它到点 A （ 3 ， 2 ）的距离之和最小，最小距离是多少？ P X y o A (3,2) F 三 . 定义法求最值 点评：将抛物线上一点到焦点的距离（即焦半径）转化为它到准线距离构造出“点到直线的垂线段最短”。 P X y o F 三 . 定义法求最值 A (0,2) 变式： 在抛物线 y 2 =2x 上求一点 P ，使得点 P 到点 A （ 0 ， 2 ）的距离与它到准线的距离之和最小 , 距离是多少？ 点评：将抛物线上一点到准线距离转化为它到焦点的距离（即焦半径），构造出“两点之间线段最短”。 三 . 定义法求最值 要注意平面几何知识的应用，如 两点之间线段最短 ， 三角形中三边间的不等关系 ， 点与直线上点的连线垂线段最短 等 点评： 重视 定义 在解题中的应用，灵活地进行抛物线上的 点到焦点距离 与 到准线的距离 的相互转化 . 课堂小结 一个知 识点：抛物线的定义 一种方法：定义法 一种思想：数形结合 通过以上的例题分析不难看出，定义对解决抛物线问题的重要性，所以对知识要溯本求源，才能融会贯通，以不变应万变。 1 、 设抛物线 的焦点为 F ，准线为 ， P 为抛物线上一点， 为垂足，如果直线 AF 的斜率为 ，那么 |PF|= 。 P F o x A K 8 强化训练 C 强化训练 3. 直线 l 过抛物线 y 2 =2px(p>0) 的焦点且与抛物线交于 A 、 B 两点，若线段 AB 的长为 8 ， AB 的中点到 y 轴的距 离是 2 ，则此抛物线的方程为 . y 2 =8x 4 ， （针对训练 2 改编） 设抛物线 x 2 =12 y 的焦点为 F ，经过点 P (2, 1) 的直线 l 与抛物线相交于 A 、 B 两点，又知点 P 恰为 AB 中点，则｜ AF ｜ + ｜ BF ｜ =________ 。 强化训练 作业： 巩固优化设计 选作限时作业 （注意同步性和讲练结合性）