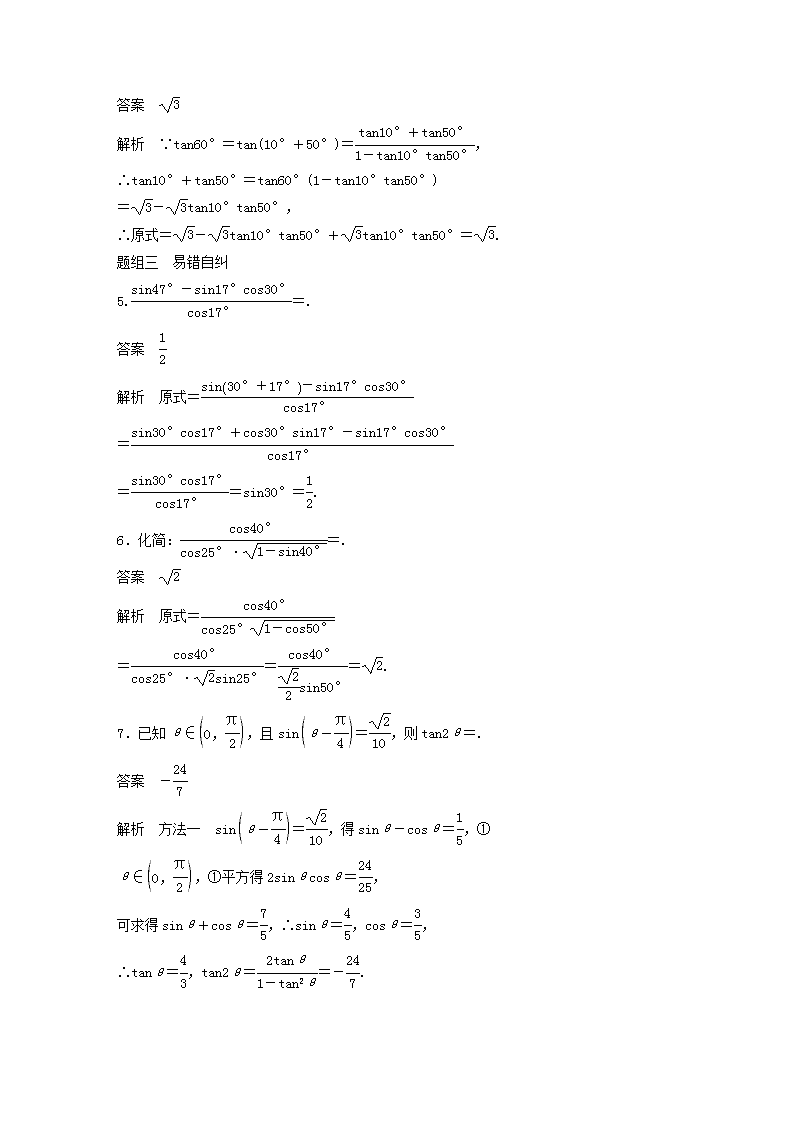【数学】2020届一轮复习人教B版简单的三角恒等变换第课时学案
§5.4 简单的三角恒等变换
最新考纲
考情考向分析
1.掌握两角和与两角差的正弦、余弦、正切公式,掌握正弦、余弦、正切二倍角的公式.
2.掌握简单的三角函数式的化简、求值及恒等式证明.
三角恒等变换是三角变换的工具,主要考查利用两角和与差的三角函数公式、二倍角公式进行三角函数的化简与求值,重在考查化简、求值,公式的正用、逆用以及变式运用,可单独考查,也可与三角函数的图象和性质、向量等知识综合考查,加强转化与化归思想的应用意识.题型选择、填空、解答均有可能出现,中低档难度.
1.两角和与差的余弦、正弦、正切公式
cos(α-β)=cosαcosβ+sinαsinβ(C(α-β))
cos(α+β)=cosαcosβ-sinαsinβ(C(α+β))
sin(α-β)=sinαcosβ-cosαsinβ(S(α-β))
sin(α+β)=sinαcosβ+cosαsinβ(S(α+β))
tan(α-β)=(T(α-β))
tan(α+β)=(T(α+β))
2.二倍角公式
sin2α=2sinαcosα;
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α;
tan2α=.
概念方法微思考
1.诱导公式与两角和差的三角函数公式有何关系?
提示 诱导公式可以看成和差公式中β=k·(k∈Z)时的特殊情形.
2.怎样研究形如f(x)=asinx+bcosx函数的性质?
提示 先根据辅助角公式asinx+bcosx=·sin(x+φ),将f(x)化成f(x)=Asin(ωx+φ)+k的形式,再结合图象研究函数的性质.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)存在实数α,β,使等式sin(α+β)=sinα+sinβ成立.( √ )
(2)对任意角α都有1+sinα=2.( √ )
(3)y=3sinx+4cosx的最大值是7.( × )
(4)公式tan(α+β)=可以变形为tanα+tanβ=tan(α+β)(1-tanαtanβ),且对任意角α,β都成立.( × )
题组二 教材改编
2.[P127T2]若cosα=-,α是第三象限的角,则sin等于( )
A.-B.C.-D.
答案 C
解析 ∵α是第三象限角,∴sinα=-=-,
∴sin=-×+×=-.
3.[P131T5]sin347°cos148°+sin77°cos58°=.
答案
解析 sin347°cos148°+sin77°cos58°
=sin(270°+77°)cos(90°+58°)+sin77°cos58°
=(-cos77°)·(-sin58°)+sin77°cos58°
=sin58°cos77°+cos58°sin77°
=sin(58°+77°)=sin135°=.
4.[P146A组T4(2)]tan10°+tan50°+tan10°tan50°=.
答案
解析 ∵tan60°=tan(10°+50°)=,
∴tan10°+tan50°=tan60°(1-tan10°tan50°)
=-tan10°tan50°,
∴原式=-tan10°tan50°+tan10°tan50°=.
题组三 易错自纠
5.=.
答案
解析 原式=
=
==sin30°=.
6.化简:=.
答案
解析 原式=
===.
7.已知θ∈,且sin=,则tan2θ=.
答案 -
解析 方法一 sin=,得sinθ-cosθ=,①
θ∈,①平方得2sinθcosθ=,
可求得sinθ+cosθ=,∴sinθ=,cosθ=,
∴tanθ=,tan2θ==-.
方法二 ∵θ∈且sin=,
∴cos=,
∴tan==,∴tanθ=.
故tan2θ==-.
8.化简:=.
答案 4sinα
解析 ===4sinα.
第1课时 两角和与差的正弦、余弦和正切公式
题型一 和差公式的直接应用
1.(2018·嘉兴检测)sin215°-cos215°的值为( )
A.B.C.-D.-
答案 C
解析 sin215°-cos215°=-(cos215°-sin215°)
=-cos30°=-,故选C.
2.已知tan=,tan=,则tan(α+β)的值为( )
A.B.C.D.1
答案 D
解析 ∵tan=,tan=,
∴tan(α+β)=tan
=
==1.
3.已知sinα=,α∈,tan(π-β)=,则tan(α-β)的值为( )
A.-B.C.D.-
答案 A
解析 ∵α∈,∴cosα=-,tanα=-,
又tanβ=-,
∴tan(α-β)=
==-.
4.计算的值为.
答案
解析 =
===.
思维升华 (1)使用两角和与差的三角函数公式,首先要记住公式的结构特征.
(2)使用公式求值,应先求出相关角的函数值,再代入公式求值.
题型二 和差公式的灵活应用
命题点1 角的变换
例1(1)设α,β都是锐角,且cosα=,sin(α+β)=,则cosβ=.
答案
解析 依题意得sinα==,
因为sin(α+β)=
α,
所以α+β∈,所以cos(α+β)=-.
于是cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-×+×=.
(2)(2018·浙江名校联盟联考)已知sin=,则cos等于( )
A.-B.C.-D.
答案 C
解析 设θ=-α,则2θ=-2α,∴2α+=π-2θ,
∴cos=cos(π-2θ)=-cos2θ=2sin2θ-1
=-1=-.
命题点2 三角函数式的变换
例2(1)化简: (0<θ<π);
(2)求值:-sin10°.
解 (1)由θ∈(0,π),得0<<,∴cos>0,
∴==2cos.
又(1+sinθ+cosθ)
=
=2cos
=-2coscosθ,
故原式==-cosθ.
(2)原式=-sin10°
=-sin10°·
=-sin10°·
=-2cos10°=
=
=
==.
引申探究
化简: (0<θ<π).
解 ∵0<θ<π,∴0<<,∴=2sin,
又1+sinθ-cosθ=2sincos+2sin2
=2sin,
∴原式=
=-cosθ.
命题点3 公式的逆用与变形
例3(1)已知sinα+cosβ=,sinβ-cosα=,则sin(α-β)=.
答案 -
解析 ∵sinα+cosβ=,sinβ-cosα=,
∴(sinα+cosβ)2=,(sinβ-cosα)2=,
即sin2α+2sinαcosβ+cos2β=,①
sin2β-2sinβcosα+cos2α=.②
①+②得sin2α+2sinαcosβ+cos2β+sin2β-2sinβcosα+cos2α=(sin2α+cos2α)+(cos2β+sin2β)+2(sinαcosβ-sinβcosα)=1+1+2sin(α-β)=2+2sin(α-β)=,则sin(α-β)=-.
(2)已知α-β=,tanα-tanβ=3,则cos(α+β)的值为.
答案 -
解析 ∵tanα-tanβ=-==3,且α-β=,∴cosαcosβ=,又cos(α-β)=cosαcosβ+sinαsinβ=,∴sinαsinβ=-,那么cos(α+β)=cosαcosβ-sinαsinβ=-.
思维升华 (1)解决三角函数的求值问题的关键是把“所求角”用“已知角”表示.①当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;②当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系.
(2)常见的配角技巧:2α=(α+β)+(α-β),α=(α+β)-β,β=-,α=+,=-等.
跟踪训练 (1)计算:
=.(用数字作答)
答案
解析 ====.
(2)已知α∈,β∈,且cosα=,cos(α+β)=-,则sinβ=.
答案
解析 由已知可得sinα=,sin(α+β)=,
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=×-×=.
(3)若sinx+cosx=,则tan=.
答案 ±
解析 由sinx+cosx=,得2sin=,即sin=,所以cos=±,所以tan=±,即tan=tan=±.
用联系的观点进行三角变换
三角变换的关键是找到条件和结论中的角和式子结构之间的联系.变换中可以通过适当地拆角、凑角或对式子整体变形达到目的.
例(1)(2018·绍兴一中期中)(1+tan21°)(1+tan20°)(1+tan25°)(1+tan24°)的值为( )
A.2B.4C.8D.16
答案 B
解析 (1+tan21°)(1+tan20°)(1+tan25°)(1+tan24°)=[1+tan(45°-24°)]·(1+tan24°)[1+tan(45°-25°)](1+tan25°)=·(1+tan24°)··(1+tan25°)=·(1+tan24°)··(1+tan25°)=4,故选B.
(2)设α为锐角,若cos=,则sin的值为.
答案
解析 ∵α为锐角且cos=>0,
∴α+∈,∴sin=.
∴sin=sin
=sin2cos-cos2sin
=sincos-
=××-
=-=.
(3)已知sinα=,α∈,则=.
答案 -
解析 =
=cosα-sinα,
∵sinα=,α∈,
∴cosα=-,∴原式=-.
1.(2018·台州模拟)已知cosα=1,则sin等于( )
A.B.C.-D.-
答案 C
解析 因为cosα=1,所以sinα=0,则sin
=sinαcos-cosαsin=-sin=-,故选C.
2.(2018·温州检测)已知α是第二象限角,且tanα=-,则sin2α等于( )
A.- B.
C.- D.
答案 C
解析 因为α是第二象限角,且tanα=-,
所以sinα=,cosα=-,
所以sin2α=2sinαcosα=2××=-,
故选C.
3.(2018·衢州模拟)设a=cos50°cos127°+cos40°sin127°,b=(sin56°-cos56°),c=,则a,b,c的大小关系是( )
A.a>b>c B.b>a>c
C.c>a>b D.a>c>b
答案 D
解析 a=sin40°cos127°+cos40°sin127°
=sin(40°+127°)=sin167°=sin13°,
b=(sin56°-cos56°)=sin56°-cos56°
=sin(56°-45°)=sin11°,
c==cos239°-sin239°=cos78°
=sin12°,
∵sin13°>sin12°>sin11°,∴a>c>b.
4.已知α为锐角,若sin=,则cos等于( )
A. B.
C. D.
答案 A
解析 由于α为锐角,且sin=,
则cos=,
则cos=cos
=coscos+sinsin
=×+×=,故选A.
5.(2018·绍兴一中期中)已知sinα=+cosα,且α∈,则的值为( )
A.-B.-C.D.
答案 A
解析 由sinα=+cosα可得sinα-cosα=,
即sin=,可得sin=>0,
又α∈,则α-∈,
可得cos==,
则=
==-2cos
=-,故选A.
6.已知cosα=,cos(α+β)=-,且α,β∈,则cos(α-β)的值为( )
A.-B.C.-D.
答案 D
解析 因为α∈,所以2α∈(0,π),
因为cosα=,所以cos2α=2cos2α-1=-,
所以sin2α==,
而α,β∈,所以α+β∈(0,π),
所以sin(α+β)==,
所以cos(α-β)=cos[2α-(α+β)]
=cos2αcos(α+β)+sin2αsin(α+β)
=×+×=.
7.已知锐角α,β满足sinα-cosα=,tanα+tanβ+tanαtanβ=,则α,β的大小关系是( )
A.α<<β B.β<<α
C.<α<β D.<β<α
答案 B
解析 ∵α为锐角,sinα-cosα=>0,∴<α<.
又tanα+tanβ+tanαtanβ=,
∴tan(α+β)==,
∴α+β=,又α>,∴β<<α.
8.(2018·杭州二中期中)若0<α<,-<β<0,cos=,cos=,则cos等于( )
A.B.-C.D.-
答案 C
解析 因为0<α<,-<β<0,
所以<+α<,<-<,
所以sin=,sin=,
所以cos=cos
=coscos+sin·sin
=×+×=,故选C.
9.的值是.
答案
解析 原式=
=
==.
10.=.
答案
解析 =
==.
11.(2018·浙江第二次联盟校联考)已知cos2=,则sin2α的值为.
答案
解析 因为cos2===,所以sin2α=.
12.已知sin(α-β)cosα-cos(β-α)sinα=,β是第三象限角,求sin的值.
解 依题意可将已知条件变形为
sin[(α-β)-α]=-sinβ=,sinβ=-.
又β是第三象限角,所以cosβ=-.
所以sin=-sin
=-sinβcos-cosβsin
=×+×=.
13.若α∈,且3cos2α=sin,则sin2α的值为( )
A.- B.
C.- D.
答案 C
解析 由3cos2α=sin可得
3(cos2α-sin2α)=(cosα-sinα),
又由α∈可知,cosα-sinα≠0,
于是3(cosα+sinα)=,
所以1+2sinαcosα=,故sin2α=-.故选C.
14.已知coscos=,求sin4θ+cos4θ的值.
解 因为coscos
=
=(cos2θ-sin2θ)=cos2θ=.
所以cos2θ=.
故sin4θ+cos4θ=2+2
=+=.
15.化简:·=.
答案 -4
解析 原式=·=·
=-4·tan(45°+15°)=-4.
16.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,求sin(2α-β)+sin(α-2β)的取值范围.
解 由sinαcosβ-cosαsinβ=1,得sin(α-β)=1,
又α,β∈[0,π],∴α-β=,
∴
即≤α≤π,
∴sin(2α-β)+sin(α-2β)
=sin+sin(α-2α+π)
=cosα+sinα=sin.
∵≤α≤π,
∴≤α+≤,
∴-1≤sin≤1,
即取值范围为[-1,1].