- 2021-05-19 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁省锦州市2021届新高考模拟化学试题(校模拟卷)含解析
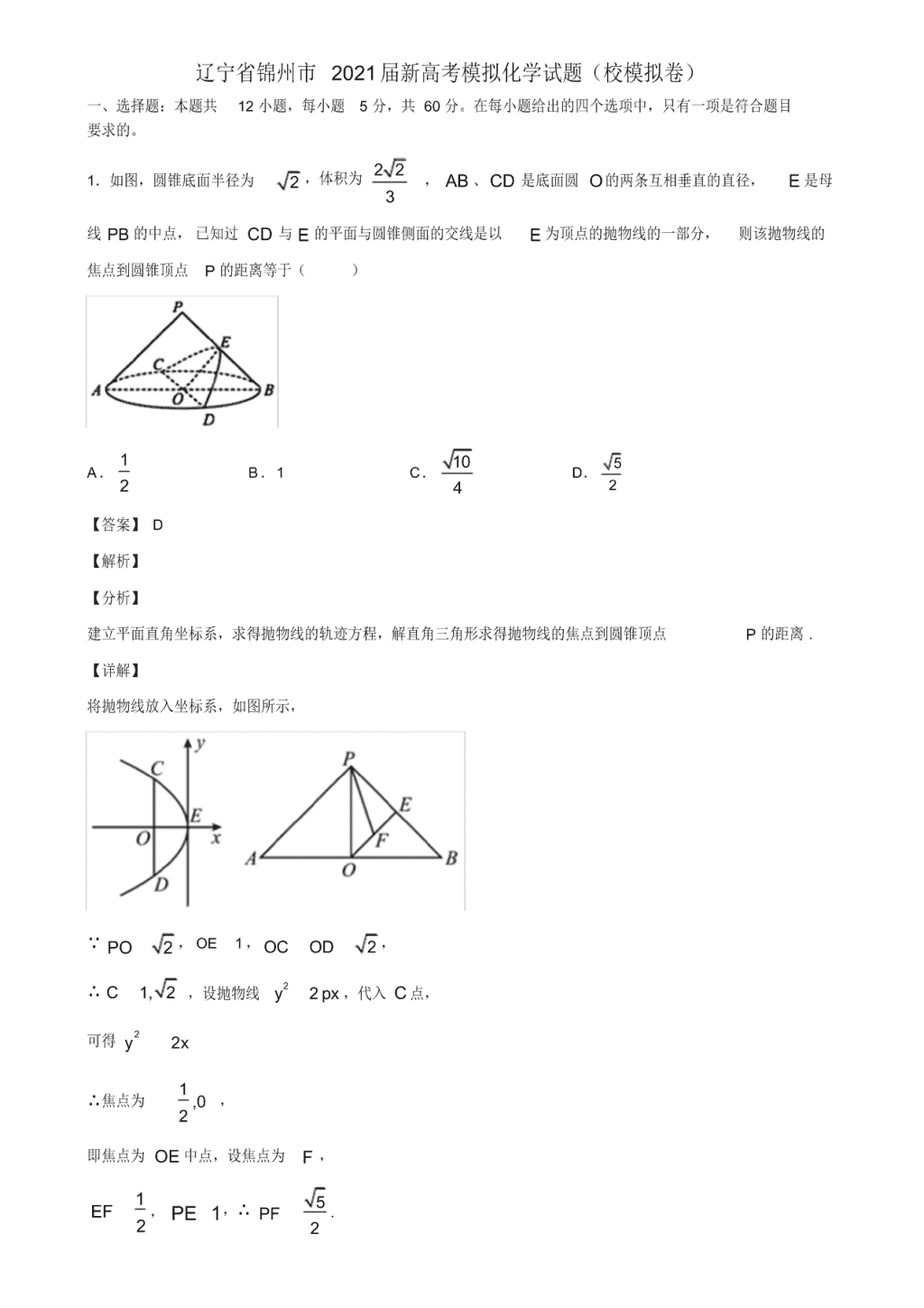
辽宁省锦州市 2021 届新高考模拟化学试题(校模拟卷) 一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目 要求的。 1.如图,圆锥底面半径为 2 ,体积为 2 2 3 , AB 、 CD 是底面圆 O的两条互相垂直的直径, E 是母 线 PB 的中点, 已知过 CD 与 E 的平面与圆锥侧面的交线是以 E 为顶点的抛物线的一部分, 则该抛物线的 焦点到圆锥顶点 P 的距离等于( ) A. 1 2 B.1 C. 10 4 D. 5 2 【答案】 D 【解析】 【分析】 建立平面直角坐标系,求得抛物线的轨迹方程,解直角三角形求得抛物线的焦点到圆锥顶点 P 的距离 . 【详解】 将抛物线放入坐标系,如图所示, ∵ 2PO , 1OE , 2OC OD , ∴ 1, 2C ,设抛物线 2 2y px ,代入 C 点, 可得 2 2y x ∴焦点为 1 ,0 2 , 即焦点为 OE 中点,设焦点为 F , 1 2 EF , 1PE ,∴ 5 2 PF . 故选: D 【点睛】 本小题考查圆锥曲线的概念,抛物线的性质,两点间的距离等基础知识;考查运算求解能力,空间想象能 力,推理论证能力,应用意识 . 2.在平面直角坐标系 xOy 中,锐角 顶点在坐标原点,始边为 x 轴正半轴,终边与单位圆交于点 5 , 5 P m ,则 sin 2 4 ( ) A. 2 10 B. 10 10 C. 7 2 10 D. 3 10 10 【答案】 A 【解析】 【分析】 根据单位圆以及角度范围,可得 m ,然后根据三角函数定义,可得 sin ,cos ,最后根据两角和的正弦 公式,二倍角公式,简单计算,可得结果 . 【详解】 由题可知: 2 25 1 5 m ,又 为锐角 所以 0m , 2 5 5 m 根据三角函数的定义: 2 5 5sin ,cos 5 5 = = 所以 4sin 2 2sin cos 5 2 2 3cos2 cos sin 5 由 sin 2 sin 2 cos cos2 sin 4 4 4 所以 4 2 3 2 2sin 2 4 5 2 5 2 10 故选: A 【点睛】 本题考查三角函数的定义以及两角和正弦公式,还考查二倍角的正弦、余弦公式,难点在于公式的计算, 识记公式,简单计算,属基础题 . 3.已知 1sin 2 4 3 ,则 sin 的值等于( ) A. 7 9 B. 2 9 C. 2 9 D. 7 9 【答案】 A 【解析】 【分析】 由余弦公式的二倍角可得, 2 7cos( ) 1 2sin 2 2 4 9 ,再由诱导公式有 cos( ) sin 2 ,所以 7sin 9 【详解】 ∵ 1sin 2 4 3 ∴由余弦公式的二倍角展开式有 2 7cos( ) 1 2sin 2 2 4 9 又∵ cos( ) sin 2 ∴ 7sin 9 故选: A 【点睛】 本题考查了学生对二倍角公式的应用,要求学生熟练掌握三角函数中的诱导公式,属于简单题 4.已知实数 ,x y 满足约束条件 1 1 2 2 0 2 2 0 x y x y x y ,则 2 3x y 的最小值是 A. 2 B. 7 2 C.1 D. 4 【答案】 B 【解析】 【分析】 【详解】 作出该不等式组表示的平面区域,如下图中阴影部分所示, 设 2 3z x y ,则 2 1 3 3 y x z ,易知当直线 2 1 3 3 y x z 经过点 D 时, z 取得最小值, 由 1 2 2 0 x x y ,解得 1 1 2 x y ,所以 1( 1, ) 2 D ,所以 min 1 72 ( 1) 3 2 2 z ,故选 B. 5.中国古代数学著作《算法统宗》中有这样一个问题; “三百七十八里关,初行健步不为难,次后脚痛递 减半,六朝才得到其关,要见每朝行里数,请公仔细算相还 . ”其意思为: “有一个人走了 378 里路,第一 天健步走行,从第二天起脚痛每天走的路程是前一天的一半,走了 6 天后到达目的地,求该人每天走的路 程 . ”由这个描述请算出这人第四天走的路程为( ) A. 6 里 B.12 里 C.24 里 D. 48 里 【答案】 C 【解析】 【分析】 设第一天走 1a 里,则 { }na 是以 1a 为首项,以 1 2 为公比的等比数列,由题意得 1 6 6 1(1 ) 2 37811 2 a S ,求 出 1 192a (里 ) ,由此能求出该人第四天走的路程. 【详解】 设第一天走 1a 里,则 { }na 是以 1a 为首项,以 1 2 为公比的等比数列, 由题意得: 1 6 6 1(1 ) 2 37811 2 a S , 解得 1 192a (里 ) , 3 4 1 1 1( ) 192 24 2 8 a a (里 ) . 故选: C. 【点睛】 本题考查等比数列的某一项的求法,考查等比数列等基础知识,考查推理论证能力、运算求解能力,考查 化归与转化思想、函数与方程思想,是基础题. 6.若复数 2 2 1 a i i ( a R )是纯虚数,则复数 2 2a i 在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【答案】 B 【解析】 【分析】 化简复数 2 2 1 a i i ,由它是纯虚数,求得 a ,从而确定 2 2a i 对应的点的坐标. 【详解】 2 2 1 a i i 2( )(1 ) 1 (1 ) (1 )(1 ) a i i a a i i i 是纯虚数,则 1 0 1 0 a a , 1a , 2 2 2 2a i i ,对应点为 ( 2,2) ,在第二象限. 故选: B. 【点睛】 本题考查复数的除法运算,考查复数的概念与几何意义.本题属于基础题. 7.若函数 3 2( ) 2 ( )f x x mx x m R 在 1x 处有极值,则 ( )f x 在区间 [0,2] 上的最大值为( ) A. 14 27 B.2 C.1 D. 3 【答案】 B 【解析】 【分析】 根据极值点处的导数为零先求出 m 的值,然后再按照求函数在连续的闭区间上最值的求法计算即可 . 【详解】 解:由已知得 2( ) 3 2 2f x x mx , (1) 3 2 2 0f m , 5 2 m ,经检验满足题意 . 3 25( ) 2 2 f x x x x , 2( ) 3 5 2f x x x . 由 ( ) 0f x 得 2 1 3 x ;由 ( ) 0f x 得 2 3 x 或 1x . 所以函数 ( )f x 在 20, 3 上递增,在 2 ,1 3 上递减,在 [1,2] 上递增 . 则 2 14( ) 3 27 f x f极大值 , (2) 2f , 由于 (2) ( )f f x 极大值 ,所以 ( )f x 在区间 [0,2] 上的最大值为 2. 故选: B. 【点睛】 本题考查了导数极值的性质以及利用导数求函数在连续的闭区间上的最值问题的基本思路,属于中档题. 8.已知三棱锥 P﹣ABC 的顶点都在球 O 的球面上, PA 2,PB 14 ,AB =4,CA =CB 10 ,面 PAB ⊥面 ABC ,则球 O 的表面积为( ) A. 10 3 B. 25 6 C. 40 9 D. 50 3 【答案】 D 【解析】 【分析】 由题意画出图形,找出 △PAB 外接圆的圆心及三棱锥 P﹣BCD 的外接球心 O,通过求解三角形求出三棱 锥 P﹣BCD 的外接球的半径,则答案可求 . 【详解】 如图;设 AB 的中点为 D; ∵PA 2 ,PB 14 , AB =4, ∴△ PAB 为直角三角形,且斜边为 AB ,故其外接圆半径为: r 1 2 AB =AD =2; 设外接球球心为 O; ∵CA = CB 10 ,面 PAB ⊥面 ABC , ∴CD ⊥ AB 可得 CD ⊥面 PAB ;且 DC 2 2 6CA AD . ∴O 在 CD 上; 故有: AO 2=OD 2+AD 2? R2=( 6 R) 2+r 2? R 5 6 ; ∴球 O 的表面积为: 4πR2=4π 2 5 50 36 . 故选: D. 【点睛】 本题考查多面体外接球表面积的求法,考查数形结合的解题思想方法,考查思维能力与计算能力,属于中 档题 . 9.设等差数列 na 的前 n 项和为 nS ,若 2 3S , 4 10S ,则 6S ( ) A. 21 B.22 C.11 D. 12 【答案】 A 【解析】 【分析】 由题意知 2 4 2 6 4, ,S S S S S 成等差数列,结合等差中项,列出方程,即可求出 6S 的值 . 【详解】 解:由 na 为等差数列,可知 2 4 2 6 4, ,S S S S S 也成等差数列, 所以 4 2 2 6 42 S S S S S ,即 62 10 3 3 10S ,解得 6 21S . 故选 :A. 【点睛】 本题考查了等差数列的性质,考查了等差中项 .对于等差数列,一般用首项和公差将已知量表示出来,继 而求出首项和公差 .但是这种基本量法计算量相对比较大,如果能结合等差数列性质,可使得计算量大大 减少 . 10.已知向量 ,a b v v 满足 | | 1,| | 3a b v v ,且 a v 与 b v 的夹角为 6 ,则 ( ) (2 )a b a b v v v v ( ) A. 1 2 B. 3 2 C. 1 2 D. 3 2 【答案】 A 【解析】 【分析】 根据向量的运算法则展开后利用数量积的性质即可 . 【详解】 2 2 3 1( ) (2 ) 2 2 3 1 3 2 2 a b a b a b a b v v v v v v v v . 故选: A. 【点睛】 本题主要考查数量积的运算,属于基础题 . 11.如图所示的程序框图,若输入 4a , 3b ,则输出的结果是( ) A. 6 B. 7 C. 5 D. 8 【答案】 B 【解析】 【分析】 列举出循环的每一步,可得出输出结果 . 【详解】 4i , 3S , 2 2S a b 不成立, 23 9S , 4 1 5i ; 2 2S a b 不成立, 29 81S , 5 1 6i ; 2 2S a b 不成立, 281 6561S , 6 1 7i ; 2 2S a b 成立,输出 i 的值为 7 . 故选: B. 【点睛】 本题考查利用程序框图计算输出结果,一般要将算法的每一步列举出来,考查计算能力,属于基础题 . 12.已知双曲线 C: 2 2 2 2 x y a b =1(a>0 ,b>0)的右焦点为 F,过原点 O 作斜率为 4 3 的直线交 C 的右支于点 A , 若 |OA|=|OF| ,则双曲线的离心率为( ) A. 3 B. 5 C.2 D. 3 +1 【答案】 B 【解析】 【分析】 以 O为圆心,以 OF 为半径的圆的方程为 2 2 2x y c ,联立 2 2 2 2 2 2 2 1 x y c x y a b ,可求出点 2 2 2 ,a c b bA c c ,则 2 2 2 4 3 b c a c b c ,整理计算可得离心率 . 【详解】 解:以 O 为圆心,以 OF 为半径的圆的方程为 2 2 2x y c , 联立 2 2 2 2 2 2 2 1 x y c x y a b ,取第一象限的解得 2 2 2 a c bx c by c , 即 2 2 2 ,a c b bA c c ,则 2 2 2 4 3 b c a c b c , 整理得 2 2 2 29 5 5 0c a c a , 则 2 2 5 1 9 c a (舍去) , 2 2 5c a , 5ce a . 故选: B. 【点睛】 本题考查双曲线离心率的求解,考查学生的计算能力,是中档题 . 二、填空题:本题共 4 小题,每小题 5 分,共 20 分。 13.已知 f x 为偶函数,当 0x 时, ( ) xf x e x ,则 (ln 2)f __________. 【答案】 2 ln2 【解析】 【分析】 由偶函数的性质直接求解即可 【详解】 ln2ln2 ln2 ln2 2 ln2f f e . 故答案为 2 ln2 【点睛】 本题考查函数的奇偶性,对数函数的运算,考查运算求解能力 14.复数 (2 )z i i (其中 i 为虚数单位)的共轭复数为 ________. 【答案】 1 2i 【解析】 【分析】 利用复数的乘法运算求出 z ,再利用共轭复数的概念即可求解 . 【详解】 由 (2 ) 2 1 1 2z i i i i , 则 1 2z i . 故答案为: 1 2i 【点睛】 本题考查了复数的四则运算以及共轭复数的概念,属于基础题 . 15.如图 ,在梯形 ABCD 中, AD ∥ 2 4BC AB BC AD, , , E F, 分别是 BC CD, 的中点,若 1AE DE uuur uuur ,则 AF CD uuur uuur 的值为 ___________. 【答案】 2 【解析】 【分析】 建系,设设 A ,由 1AE DE uuur uuur 可得 3 ,进一步得到 C F、 的坐标,再利用数量积的坐标运算 即可得到答案 . 【详解】 以 A 为坐标原点, AD 为 x 轴建立如图所示的直角坐标系,设 A ,则 (4,0), (2cos ,2sin ), (1 2cos ,2sin ), (2 2cos ,2sin )D B E C , 所以 AE uuur (1 2cos ,2sin ) , DE uuur (2cos 3,2sin ) ,由 1AE DE uuur uuur , 得 2(1 2cos )(2cos 3) 4sin 1 ,即 1cos 2 ,又 [0, ] ,所以 3 ,故 7 3(3, 3), ( , ) 2 2 C F , 7 3(1, 3), ( , ) 2 2 CD AF uuur uuur , 所以 7 33 2 2 2 AF CD uuur uuur . 故答案为: 2 【点睛】 本题考查利用坐标法求向量的数量积,考查学生的运算求解能力,是一道中档题 . 16.春天即将来临,某学校开展以 “拥抱春天,播种绿色 ”为主题的植物种植实践体验活动.已知某种盆栽 植物每株成活的概率为 p ,各株是否成活相互独立.该学校的某班随机领养了此种盆栽植物 10 株,设 X 为其中成活的株数,若 X 的方差 2.1DX , ( 3) ( 7)P X P X ,则 p ________. 【答案】 0.7 【解析】 【分析】 由题意可知: X ~ B 10, p ,且 10 1 2.1 3 7 p p P X P X ,从而可得 p 值. 【详解】 由题意可知: X ~ B 10, p ∴ 10 1 2.1 3 7 p p P X P X ,即 2100 100 21 0 0.5 p p p , ∴ 0.7p 故答案为: 0.7 【点睛】 本题考查二项分布的实际应用,考查分析问题解决问题的能力,考查计算能力,属于中档题. 三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.设 O 为坐标原点, 动点 M 在椭圆 C : 2 2 2 1(1 5)x y a a 上, 该椭圆的左顶点 A 到直线 5 0x y 的距离为 3 2 2 . ( 1)求椭圆 C 的标准方程; ( 2)若椭圆 C 外一点 N 满足, MN uuuuv 平行于 y 轴, ( 2 ) =0ON OM MN uuuv uuuuv uuuuv ,动点 P 在直线 2 3x 上, 满足 2ON NP uuuv uuuv .设过点 N 且垂直 OP 的直线 l ,试问直线 l 是否过定点?若过定点,请写出该定点,若 不过定点请说明理由 . 【答案】 (1) 2 2 1 4 x y ;(2)见解析 【解析】 【分析】 ( 1)根据点到直线的距离公式可求出 a 的值,即可得椭圆方程; ( 2)由题意 M(x0,y0),N( x0,y1),P(2 3 ,t),根据 2 0ON OM MN uuuv uuuuv uuuuv ,可得 y1=2y0,由 2ON NP uuuv uuuv , 可得 2 3 x0+2y 0t=6,再根据向量的运算可得 ? 0NF OP uuuv uuuv ,即可证明. 【详解】 ( 1)左顶点 A 的坐标为(﹣ a,0),∵ = ,∴ |a﹣5|=3,解得 a=2 或 a=8(舍去) ,∴椭 圆 C 的标准方程为 +y 2=1, ( 2)由题意 M (x0, y0),N(x0,y1),P(2 ,t),则依题意可知 y1≠y0, ON 2OM MN 0 uuuv uuuuv uuuuv Q 得 ( x0﹣2 x0,y1﹣2y0) ? (0,y1﹣y0)=0,整理可得 y1=2y0,或 y1=y0 (舍), ON NP 2 uuuv u Q uuv ,得( x0, 2y0)(2 ﹣x0,t﹣2y0)= 2,整理可得 2 x0+2y 0t=x02+4y 02+2=6,由( 1)可得 F( ,0),∴ = ( ﹣ x0,﹣ 2y0),∴ ? =( ﹣x0,﹣ 2y0)(2 , t)= 6﹣2 x0﹣2y 0t=0,∴ NF ⊥OP ,故过 点 N 且垂直于 OP 的直线过椭圆 C 的右焦点 F. 【点睛】 本题考查了椭圆方程的求法,直线和椭圆的关系,向量的运算,考查了运算求解能力和转化与化归能力, 属于中档题 . 18.在锐角 ABCV 中, , ,a b c 分别是角 , ,A B C 的对边, 2 ,cosm b c Cr , ,cosn a Ar ,且 //m nr r . ( 1)求角 A的大小; ( 2)求函数 22sin cos 2 3 y B B 的值域. 【答案】 (1) 3 A ;(2) 3, 2 2 【解析】 【分析】 ( 1)由向量平行的坐标表示、正弦定理边化角和两角和差正弦公式可化简求得 cos A,进而得到 A ; ( 2)利用两角和差余弦公式、二倍角和辅助角公式化简函数为 1 sin 2 6 y B ,根据 B 的范围可确 定 2 6 B 的范围,结合正弦函数图象可确定所求函数的值域 . 【详解】 ( 1) //m nr rQ , 2 cos cos 0b c A a C , 由正弦定理得: 2sin sin cos sin cos 0B C A A C , 即 2sin cos sin 2sin cos sin 0B A A C B A B , 0, 2 BQ , sin 0B , 1cos 2 A , 又 0, 2 A , 3 A . ( 2)在锐角 ABCV 中, 3 A , 6 2 B . 2 1 32sin cos 2 1 cos2 cos2 sin 2 3 2 2 y B B B B B 3 11 sin 2 cos2 1 sin 2 2 2 6 B B B . 6 2 BQ , 52 6 6 6 B , 1 sin 2 1 2 6 B , 3 2 2 y , 函数 2sin 2 cos 2 3 y B B 的值域为 3 ,2 2 . 【点睛】 本题考查三角恒等变换、解三角形和三角函数性质的综合应用问题;涉及到共线向量的坐标表示、利用三 角恒等变换公式化简求值、正弦定理边化角的应用、正弦型函数值域的求解等知识 . 19.如图,三棱柱 ABC-A 1B 1C 1 中,侧面 BCC 1B 1是菱形, AC=BC=2 ,∠CBB 1= 3 ,点 A 在平面 BCC 1B1 上的投影为棱 BB 1 的中点 E. ( 1)求证:四边形 ACC 1A 1 为矩形; ( 2)求二面角 E-B 1C-A 1 的平面角的余弦值. 【答案】 (1)见解析( 2) 21 7 【解析】 【分析】 ( 1)通过勾股定理得出 1CE BB ,又 1AE BB ,进而可得 1BB 平面 AEC ,则可得到 1AA AC , 问题得证; ( 2)如图,以 E 为原点, EC , 1EB , EA 所在直线分别为 x 轴, y 轴, z 轴,求出平面 1EB C 的法向量 和平面 1 1A B C 的法向量,利用空间向量的夹角公式可得答案 . 【详解】 ( 1)因为 AE ⊥ 平面 1 1BBC C ,所以 1AE BB , 又因为 1 1 1 2 BE BB , 2BC , 3 EBC ,所以 3CE , 因此 2 2 2BE CE BC ,所以 1CE BB , 因此 1BB 平面 AEC ,所以 1BB AC , 从而 1AA AC ,又四边形 1 1ACC A 为平行四边形, 则四边形 1 1ACC A 为矩形; ( 2)如图,以 E 为原点, EC , 1EB , EA 所在直线分别为 x 轴, y 轴, z 轴,所以 1 1(0,0,1), (0,2,1), (0,1,0), ( 3,0,0)A A B C , 平面 1EB C 的法向量 (0,0,1)m ur ,设平面 1 1A B C 的法向量 ( , , )n x y z r , 由 1 ( , , ) ( 3,1,0) 0 3n CB x y z y x r uuur , 由 1 1 ( , , ) (0,1,1) 0 0n B A x y z y z r uuuur , 令 1 3, 3x y z ,即 (1, 3, 3)n r , 所以, 3 21cos , 71 7 m n ur r , 所以,所求二面角的余弦值是 21 7 . 【点睛】 本题考查空间垂直关系的证明,考查向量法求二面角的大小,考查学生计算能力,是中档题 . 20.如图,在正四棱锥 P ABCD 中, 2PA AB ,点 M 、 N 分别在线段 PA 、 BD 上, 1 3BN BD . ( 1)若 1 3PM PA,求证: MN ⊥ AD ; ( 2)若二面角 M BD A 的大小为 4 ,求线段 MN 的长. 【答案】 (1)证明见解析; (2) 22 6 . 【解析】 试题分析:由于图形是正四棱锥,因此设 AC 、BD 交点为 O,则以 OA 为 x 轴正方向,以 OB 为 y 轴正 方向, OP 为 z 轴正方向建立空间直角坐标系,可用空间向量法解决问题. (1)只要证明 MN AD uuuur uuur =0 即 可证明垂直; (2)设 4 4 0 4 2 2 0 a b a c = λ 2 2 2 2 2 2 0 2 1 1 1 1 220 0 0 0, ,0 1 0 4 2 2 3 2 3 61 y x y z ,得 M(λ, 0,1-λ),然后求出平面 MBD 的法向量 n r ,而平面 ABD 的法向量为 OP uuur ,利用法向量夹角与二面角相等 或互补可求得 λ. 试题解析 : (1) 连结 AC 、BD 交于点 O,以 OA 为 x 轴正方向,以 OB 为 y 轴正方向, OP 为 z 轴正方向建 立空间直角坐标系. 因为 PA=AB = 2 , 则 A(1 ,0,0),B(0 ,1, 0), D(0,- 1,0),P(0,0,1). 由 BN uuur = 1 3 BD uuur ,得 N 10, ,0 3 , 由 PM uuuur = 1 3 PA uuur ,得 M 1 2,0, 3 3 , 所以 1 1 1 2, , 3 3 3 3 MN uuuur , AD uuur =(- 1,- 1,0). 因为 MN AD uuuur uuur =0,所以 MN ⊥AD (2) 解:因为 M 在 PA 上,可设 PM uuuur =λPA uuur ,得 M(λ,0,1-λ). 所以 BM uuuur = ( λ,- 1, 1-λ), BD uuur =(0,- 2,0). 设平面 MBD 的法向量 n r =(x,y,z), 由 0 0 n BD n BM r uuur r uuuur ,得 2 0 1 0 y x y z 其中一组解为 x= λ-1,y=0,z=λ,所以可取 n r =( λ-1,0,λ). 因为平面 ABD 的法向量为 OP uuur =(0,0,1), 所以 cos 4 = n OP n OP r uuur r uuur ,即 2 2 = 2 21 ,解得 λ= 1 2 , 从而 M 1 1,0, 2 2 , N 10, ,0 3 , 所以 MN = 2 2 2 1 1 10 0 0 2 3 2 = 22 6 . 考点:用空间向量法证垂直、求二面角. 21.某广告商租用了一块如图所示的半圆形封闭区域用于产品展示 ,该封闭区域由以 O 为圆心的半圆及直 径 AB 围成.在此区域内原有一个以 OA为直径、 C 为圆心的半圆形展示区 ,该广告商欲在此基础上 ,将其 改建成一个凸四边形的展示区 COPQ ,其中 P 、 Q 分别在半圆 O与半圆 C 的圆弧上 ,且 PQ 与半圆 C 相切 于点 Q .已知 AB 长为 40 米,设 BOP为 2 .(上述图形均视作在同一平面内) ( 1)记四边形 COPQ 的周长为 f ,求 f 的表达式 ; ( 2)要使改建成的展示区 COPQ 的面积最大 ,求 sin 的值. 【答案】 (1) 40 20 2 cosf , 0, 2 .(2) 34 2 8 【解析】 【分析】 ( 1)由余弦定理的 2PC ,然后根据直线与圆相切的性质求出 PQ ,从而求出 f ; ( 2)求得 S 的表达式 ,通过求导研究函数的单调性求得最大值 . 【详解】 解:( 1)连 PC .由条件得 0, 2 . 在三角形 POC 中 , 10OC , 20OP , POC ,由余弦定理 ,得 2 2 2 2 cos 2 100 5 4cos2PC OC OP OC OP , 因为 PQ 与半圆 C 相切于 Q ,所以 CQ PQ , 所以 2 2 2 400 1 cos2PQ PC CQ ,所以 20 2 cosPQ . 所以四边形 COPQ 的周长为 40 20 2 cosf CO OP PQ QC , 0, 2 . ( 2)设四边形 COPQ 的面积为 S ,则 100 2 cos 2sin cosOCP QCPS S S△ △ , 0, 2 . 所以 2 2100 2sin 2cos 2sin 100 4sin 2 sin 2S , 0, 2 . 令 0S t ,得 34 2sin 8 列表: sin 34 2(0, ) 8 34 2 8 34 2( ,1) 8 S + 0 - S 增 最大值 减 答:要使改建成的展示区 COPQ 的面积最大 ,sin 的值为 34 2 8 . 【点睛】 本题考查余弦定理、直线与圆的位置关系、导数与函数最值的关系 ,考查考生的逻辑思维能力 ,运算求解能 力 ,以及函数与方程的思想 . 22.已知椭圆: 2 2 2 2: 1x yC a b ( 0a b ),四点 1 11P , , 2 01P , , 3 21 2 P , , 4 21 2 P , 中恰 有三点在椭圆 C 上 . ( 1)求椭圆 C 的方程; ( 2)设椭圆 C 的左右顶点分别为 A B, . P 是椭圆 C 上异于 A B, 的动点,求 APB 的正切的最大值 . 【答案】 (1) 2 2 1 2 x y ;(2) 2 2 【解析】 【分析】 ( 1)分析可得 3 4P P, 必在椭圆 C 上, 11, 不在椭圆 C 上,代入即得解; ( 2)设直线 PA,PB 的倾斜角分别为 , ,斜率为 1 2k k, ,可得 1 2 1 2 k k .则 AFB , 2 1 1 2 tan 1 k kAPB k k ,利用均值不等式,即得解 . 【详解】 ( 1)因为 3 4P P, 关于轴对称, 所以 3 4P P, 必在椭圆 C 上, 2 2 2 211 1 1 1 2a b a b ∴ 11, 不在椭圆 C 上 ∴ 1b , 2 2a , 即 2 2 1 2 x y . ( 2)设椭圆上的点 0 0( , )P x y ( 0 2x ), 设直线 PA,PB 的倾斜角分别为 , ,斜率为 1 2k k, 又 2 2 0 02 2x y ∴ 0 0 1 2 0 0 1 22 2 y yk k x x . AFB , 1 tank , 2 tank (不妨设 b a> ) . 故 1 20, 0k k tan tanAPB 2 1 1 21 k k k k 2 2 12 2 k k 2 2 12[( ) ( )] 2 k k 2 2 当且仅当 2 2 1 2 k k ,即 2 2 2 k 时等号成立 【点睛】 本题考查了直线和椭圆综合,考查了学生综合分析,转化划归,数学运算的能力,属于较难题 . 23.a,b,c 分别为 △ABC 内角 A ,B,C 的对边 .已知 a=3, sin sin sinc C a A b B ,且 B= 60°. ( 1)求 △ABC 的面积; ( 2)若 D,E 是 BC 边上的三等分点,求 sin DAE . 【答案】 (1) 9 3 2 ;(2) 3 651 434 【解析】 【分析】 ( 1)根据正弦定理,可得 △ABC 为直角三角形,然后可计算 b,可得结果 . ( 2)计算 ,AE AD ,然后根据余弦定理,可得 cos DAE ,利用平方关系,可得结果 . 【详解】 ( 1) △ABC 中,由 csinC =asinA+bsinB , 利用正弦定理得 c2=a2+b2,所以 △ABC 是直角三角形 . 又 a=3, B=60°,所以 tan60 3 3b a o ; 所以 △ABC 的面积为 1 9 3 2 2 S ab . ( 2)设 D 靠近点 B,则 BD=DE =EC=1. 2 2 2 7AE b CE , 2 2 31AD b CD 所以 2 2 2 29 217cos 2 434 AE AD DEDAE AE AD 所以 3 651sin 1 cos 434 DAE DAE . 【点睛】 本题考查正弦定理的应用,属基础题 .查看更多