- 2021-05-12 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学总复习集合与常用逻辑用语
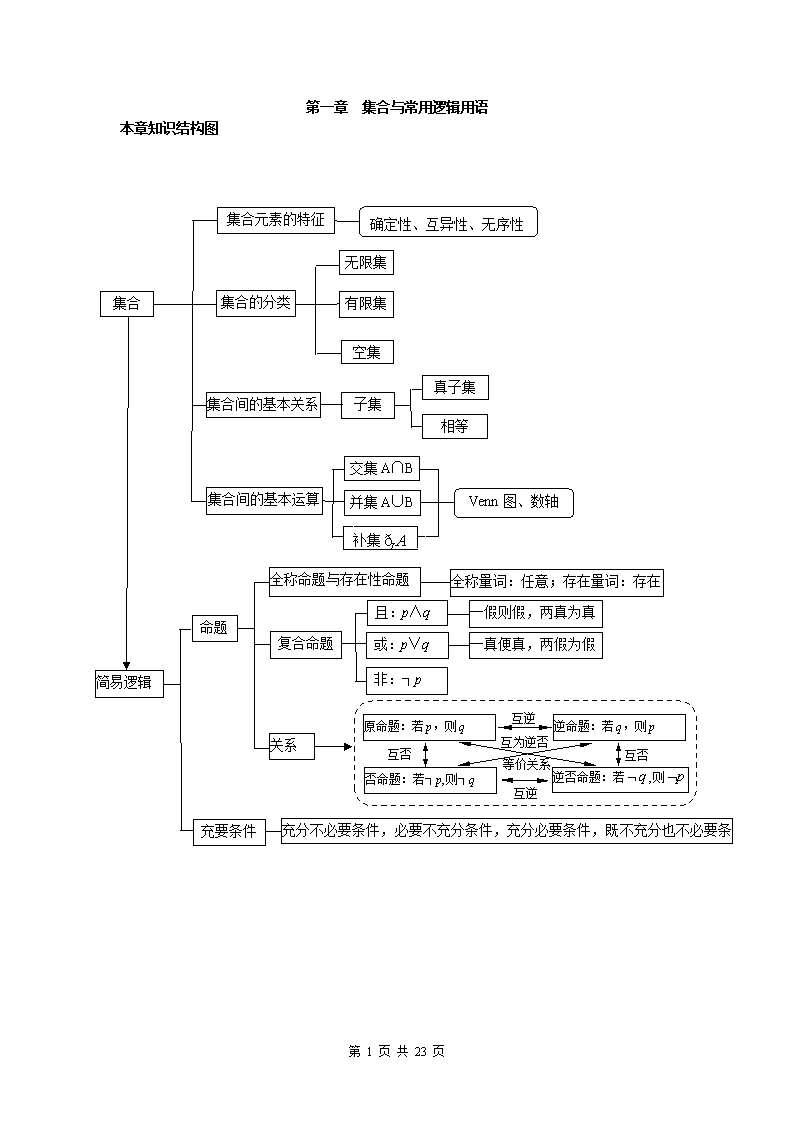
第一章 集合与常用逻辑用语 本章知识结构图 互逆 互为逆否 互逆 互否 互否 等价关系 关系 原命题:若p,则q 逆命题:若q,则p 否命题:若┐p,则┐q 逆否命题:若,则 集合 集合元素的特征 确定性、互异性、无序性 集合的分类 无限集 有限集 空集 集合间的基本关系 子集 真子集 相等 集合间的基本运算 交集A∩B 并集A∪B Venn图、数轴 充要条件 充分不必要条件,必要不充分条件,充分必要条件,既不充分也不必要条件 简易逻辑 命题 全称命题与存在性命题 全称量词:任意;存在量词:存在 复合命题 且:p∧q 或:p∨q 非:┐p 一假则假,两真为真 一真便真,两假为假 补集 第 23 页 共 23 页 第一节 集 合 考纲解读 1.集合的含义与表示.了解集合的含义、元素与集合的关系;能用自然语言、图形语言和集合语言(列举法或描述法)描述不同的具体问题. 2.集合间的基本关系.理解集合之间包含与相等的含义.能识别给定集合的子集;在具体的情境中,了解全集与空集的含义. 3.集合的基本运算.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;理解在给定集合中一个子集的含义,会求给定子集的补集;能使用韦恩(Venn)图表达集合的关系及运算. 命题趋势探究 有关集合的高考试题,考查重点是集合与集合之间的关系与运算,考试形式多以一道选择题为主,分值5分.近年来试题加强了对集合计算和化简能力的考查,并向无限集方向发展,考查学生的抽象思维能力,在解决这些问题时,要注意运用数轴法和特殊值法解题,应加强集合表示方法的转化和化简的训练. 预测2019年高考,将继续体现本章知识的工具性作用,多以小题形式出现,也有可能会将其渗透在解答题的表达之中,相对独立.具体估计为: (1)以选择题或填空题形式出现.北京、重庆等地也可能以集合为基础,综合其他知识在最后一题的位置出现.考查学生的综合推理能力. (2)热点是集合间的基本运算、数轴法的应用和体现集合的语言工具作用. 知识点精讲 一、集合的有关概念 1.集合的含义与表示 某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象. 2.集合元素的特征 (1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素. (2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现. (3)无序性:集合与其组成元素的顺序无关.如. 3.集合的常用表示法 集合的常用表示法有列举法、描述法、图示法(韦恩图、数轴)和区间法. 4.常用数集的表示 R一实数集 Q一有理数集 Z一整数集 N一自然数集或一正整数集 C一复数集 二、集合间的关系 1.元素与集合之间的关系 元素与集合之间的关系包括属于(记作)和不属于(记作)两种. 空集:不含有任何元素的集合,记作. 2.集合与集合之间的关系 (1)包含关系. 子集:如果对任意,则集合是集合的子集,记为或,显然.规定:. 第 23 页 共 23 页 (2)相等关系. 对于两个集合与,如果,同时,那么集合与相等,记作. (3)真子集关系. 对于两个集合与,若,且存在,但,则集合是集合的真子集,记作或.空集是任何集合的子集,是任何非空集合的真子集. 三、集合的基本运算 集合的基本运算包括集合的交集、并集和补集运算,如表所示. 表 交集 A B 并集 A B 补集 A I 1.交集 由所有属于集合且属于集合的元素组成的集合,叫做与的交集,记作,即. 2.并集 由所有属于集合或属于集合的元素组成的集合,叫做与的并集,记作,即. 3.补集 已知全集,集合,由中所有不属于的元素组成的集合,叫做集合相对于全集的补集,记作,即. 四、集合运算中常用的结论 1.集合中的逻辑关系 (1)交集的运算性质. ,, ,,. (2)并集的运算性质. ,, ,,. (3)补集的运算性质. ,, ,. 第 23 页 共 23 页 补充性质:. (4)结合律与分配律. 结合律: . 分配律: . (5)反演律(德摩根定律). . 即“交的补补的并”,“并的补补的交”. 2.由个元素组成的集合的子集个数 的子集有个,非空子集有个,真子集有个,非空真子集有个. 3.容斥原理 . 题型归纳及思路提示 题型1 集合的基本概念 思路提示:利用集合元素的特征:确定性、无序性、互异性. 例1.1 设,集合,则( ) A. B. C. D. 解析:由题意知,又,故,得,则集合,可得,故选C。 变式1 (2012新课标理1)已知集合,则中所含元素的个数为( ). A. B. C. D. 变式2 (2013山东理2)已知集合中元素的个数为( ). A. B. C. D. 变式3 若集合,则 , . 题型2 集合间的基本关系 思路提示 (1)判断两集合的关系常用两种方法:一是逻辑分析法,即先化筒集合,再从表达式中寻找两集合的关系;二是用列举法表示各集合,从元素中寻找关系,这体现了合情推理的思维方法. 第 23 页 共 23 页 (2)已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素的关系,进而转化为参数满足的关系,解决这类问题常利用数轴和韦恩图辅助分析. 一、集合关系中的判断问题 例1.2 若,则,,之间的关系为( ). A. B. C. D. 解析:解法一:集合中元素,故集合,而集合中元素,故. 解法二:列举,.因此,故选C. 评注:解法一是数学中“求同比异”的思想,值得学习;解法二是列举法,易于入手,也是做选择题的常用方法. 变式1 设集合,,则 A. B. C. D. 例1.3 设. (1)若,试判断集合与集合的关系; (2)若,求实数组成的集合. 分析:(1)先求集合,再由求集合,确定与的关系. (2)解方程,建立的关系式求,从而确定集合. 解析:(1)由得或,所以. 若,得,即,所以,故. (2)因为,又. ①当时,则方程无解,则; ②当时,则,由,得,所以或,即或 故集合. 评注:(1)研究集合的子集问题时应首先想到空集,因为空集是任何集合的子集. 第 23 页 共 23 页 (2)含参数的一元一次方程解的确定: 当时,方程有唯一实数解; 当时,方程有无数多个解,可为为任意实数; 当且时,方程无解. 变式1 已知集合,集合,若,求实数的取值范围. 二、已知集合间的关系,求参数的取值范围 例1.4 (2012大纲全国理2)已知集合,则( ) A.或 B.或 C.或 D.或 解析:由,得,故或且,所以或.故选B. 变式1 已知集合,若,则实数的取值范围是 . 变式2 已知集合,且,则实数的取值范围是 . 变式3 已知集合,若,则的取值范围是( ) A. B. C. D. 三、集合关系中的子集个数问题 例1.5 已知集合,则集合的子集个数为 . 分析:本题应首先确定集合中元素的个数,再求其子集的个数. 解析:集合,共8个元素,则集合的子集的个数为. 例1.6 已知集合,满足条件的集合的个数为( ) A. B. C. D. 解析:由且,得集合是集合与集合的任一子集的并集,即求集合的子集的个数为,故选D. 变式1 已知集合满足,求集合的个数. 第 23 页 共 23 页 题型3 集合的运算 思路分析 凡是遇到集合的运算(并、交、补)问题,应注意对集合元素属性的理解,数轴和韦恩图是集合交、并、补运算的有力工具,数形结合是解集合运算问题的常用思想. 一、集合元素属性的理解 例1.7 已知集合,则( ) A. B. C. D. 分析:在进行集合运算之前,首先要识别集合,即认清集合中元素的属性,判断、是数集还是点集,是数集要化简集合,是点集要解方程组.在本题中,集合代表元素是因变量,故是函数的值域(数集);集合的代表元素是自变量,故是函数的定义域(数集). 解析:,,即,所以,故选C. 评注:几量遇到集合的运算(交、并、补)问题,应注意对集合元素属性的识别,如集合是函数的值域,是数集,求出值域可以使之简化;集合是点集,表示函数图像上所有点的集合.再如集合,可以理解为单位圆上点的纵坐标的取值集合,表示的是数集;表示的是曲线,即抛的线上所有点构成的集合,它表示的是点集,故有.另如,则有,而易错为. 变式1 集合,则( ). A. B. C. D. 变式2 已知集合,则集合 . 变式3 设全集,集合,那么( ) 第 23 页 共 23 页 A. B. C. D. 变式4 已知集合,,若,求实数的取值范围. 二、数轴在集合运算中的应用 例1.8 设集合,则的取值范围是( ) A. B. C. D. 分析:借助数轴表示集合和集合,根据集合的关系,求解参数的取值范围. 解析:因为,集合,在数轴上的表示如图1-1所示.因为,所以,可得.故选A. 图1—1 变式1 (2012天津理11)已知集合,集合,且,则 , . 变式2 已知全集,集合,那么集合( ). A. B. C. D. 变式3 已知集合,则集合( ). A. B. C. D. 三、韦恩图在集合运算中的应用 例1.9 设为全集,,是两个非空集合,定义与的差集,则( ). 第 23 页 共 23 页 A. B. C. D. 分析:本题可利用题中所给定义表示从集合中去掉属于集合的元素解题. 解析:①当时,根据题意利用韦恩图解题,如图1-2所示,. ②当时,. 综上,.故选B. 评注:凡是遇到抽象的集合运算题尝试利用韦恩图求解.本题也可用举例法求解,比如,根据定义得出所求集合为空集.故选B. 变式1 设全集,,则( ). A. B. C. D. 变式2 某班级共有30人,其中15人喜爱篮球,8人喜爱足球,两项都不喜爱的有8人,则喜爱篮球但不喜爱足球的有 人. 例1.10 如图1-3所示,是全集,是它的子集,则阴影部分所表示的集合是( ) A. B. C. D. 第 23 页 共 23 页 分析:本题考查对利用韦恩图表述集合关系的理解. 解析:图1-3中的阴影部分为与的公共部分,即中去掉属于的那部分元素后剩余元素组成的集合,即,故选B. 对于韦恩图表述的集合应做如下理解:阴影部分涉及到谁就交谁,涉及不到谁就交其补集. 如图1-4所示分别表示:(a);(b);(c) 或. 变式1 已知为集合的非空子集,且不相等,若,则( ) A. B. C. D. 四、以集合为载体的创新题 例1.11 设是整数集的一个非空子集,对于,如果且,那么称是的一个孤立元,给定,由的3个元素组成的所有集合中,不含孤立元的集合共有 个. 解析:由孤立元的定义,若不是的孤立元,应满足或,即集合中元素连续,故满足的3个元素构成的不含孤立元的集合分别为、、、、和,共6个. 评注:由的3元素组成的集合中,含有一个孤立元的集合有30个,含有3个孤立元的集合有20个. 变式1 设是整数集的非空子集,如果,有,则称关于数的乘法是封闭的,若是的两个不相交的非空子集,,且,有,,有,则下列结论恒成立的是( ) 第 23 页 共 23 页 A.中至少有一个关于乘法是封闭 B.中至多有一个关于乘法是封闭 C.中有且只有一个关于乘法是封闭 D.中每一个关于乘法是封闭 变式2 已知集合,其中,由中的元素构成两个相应的集合,,其中是有序数对,集合和中的元素个数分别为和.若对于任意的,总有,则称集合具有性质. (1)检验集合与是否具有性质,并对具有性质的集合,写出相应的集合和; (2)对任何具有性质的集合,证明:. 变式3 (2012江苏23)变式3设集合,记为同时满足下列条件的集合的个数. ①; ②若,则; ③若,则. (1)求; (2)求的解析式(用表示). 最有效训练题1(限时45分钟) 1.设集合,则等于( ) A. B. C. D. 2.若,则( ) A. B. C. D. 3.设全集.集合,,那么如图1-5所示的阴影部分表示的集合是( ) A. B. C. D. 第 23 页 共 23 页 A B U 图 1—5 4.已知全集,集合,并且,那么的取值范围是( ) A. B. C. D. 5.设集合.若,则实数的取值范围是( ) A. B. C. D. 6.设全集, ,那么的充要条件是( ) A.且 B.且 C.且 D.且 7.设集合,则实数 . 8.已知集合满足条件:当时,总有(且).已知,则集合中所有元素的积等于 . 9.已知集合满足,且.若,则的取值范围是 . 10.已知集合.若,则实数的取值范围是 . 11.已知集合,若对任意的,求证:. 12.已知集合,对于中的一个子集,若存在不大于的正整数数,使得对中的任意一对元素,都有,则称具有性质. 第 23 页 共 23 页 (1)当时,试判断集合和是否具有性质?请说明理由. (2)若集合具有性质,那么集合是否一定具有性质?请说明理由. 第 23 页 共 23 页 参考答案 第一章 集合与常用逻辑用语 例1.1变式1 解析:利用集合的概念及其表示求解,注意元素的特性。 因为所以即,B中所含元素的个数为10.故选D 例1.1变式2 解析:逐个列举可得,时,时,时, 根据集合中元素的互异性可知集合B中元素为-2,-1,0,1,2,共5个,故选C 例1.1变式3 解析:依题意得,故即,因此 若则故因此x=y=1与题意不符; 若则显然与题意不符,故,此时满足题意。 例1.2变式1 解析 集合M中的元素,分子为奇数;集合N中的元素,分子为整数,则M N,故选B. 例1.3变式1 解析 由,得,若则 (1)当B=,即时,解得 (2)当B时,如图1-9所示,由,得,得 综上所述,实数的取值范围是 第 23 页 共 23 页 评注:由,勿忘B=(空集是任何集合的子集) 例1.4变式1 解析 由,如图1-10所示得,故实数的取值范围是 评注 端点值的判断通常是初学者的难题,我们可用假设法帮助判断,即假设参数取端点后,与已知吻合,假设成立;若与已知不吻合,则假设不成立。 例1.4变式2 解析 如图1-11所示,A为,B为,要使,只需,故实数的取值范围是 例1.4变式3 解析 由,得,则,故选C. 例1.6变式1 解析 由知,集合M是集合的任一非空子集与集合的并集,所以集合M的个数为28-1=255 评注求有限集的子集个数问题,有以下结论: 结论1 :含有n个元素的集合的子集个数为,真子集个数为2n-1,非空子集个数为2n-1,非空真子集个数为2n-2 ) 结论2设,则有, 第 23 页 共 23 页 ①满足的集合A的个数是 ②满足的集合A的个数是-1 ③满足的集合A的个数是-1 ④满足的集合A的个数是-2 例1.7变式1 分析 本题考查集合的概念与运算。 解析 先化简再求交集,由已知得,故,故选B 评注:本题若忽视集合P中元素的属性,易误将集合P等同于集合 例1.7变式2 解析 ,利用零点分段法解绝对值不等式。 当时,; 当时,,恒成立; 当时,, 综上所述, 又因为,由基本不等式得, 当时取,所以,故 例1.7变式3 解析 解法一:M表示直线y=x+1上除去点(2,3)的部分,表示点(2,3)和除去直线y=x+1的部分,表示直线y=x+1上的点集,所以表示的点集中仅有点(2,3),即(2,3)。 解法二 :,故选B 第 23 页 共 23 页 例1.7变式4 分析本题的几何背景是:抛物线与线段有公共点,求实数的取值范围。 解析 解法一 :问题等价于方程组在[0,2]上有解,即在[0,2]上有解,令,则由知,抛物线过点(0,1), 所以抛物线在[0,2]上与x轴有交点等价于 ① 或 ② 由①得,由②得 所以实数的取值范围为 解法二:同解法一,问题等价于方程在[0,2]上有解,故可以转化为函数值域问题。等价转化为,当时,方程不成立;当时,方程转化为;当时,函数,即当时原方程有解,由,即所求实数的取值范围为. 例1.8变式1 解析 先求出集合A,再根据集合的交集运算求解。 因为,当时,不符合题意,所以,即,又,所以. 例1.8变式2 解析 ,故选D 第 23 页 共 23 页 例1.8变式3 解析 解法一:,所以,得. 解法二: . 故选D 例1.9变式1 解析 由可得集合N中不含元素2,4,由排除法可知选项B正确,故选B. 例1.9变式2 分析 本题中的集合关系比较抽象,可以考虑使用韦恩图求解。 解析作出韦恩图,如图1-12所示,设所求为人,则喜爱篮球又喜爱足球的有15-人,喜爱足球不喜爱篮球的有人,故有. 例1.10变式1 解析 如图1-13所示,因为,所以,所以,故选A 例1.11变式1 解析 由于,故整数1一定在T,V两个集合中的一个中,不妨设,则 第 23 页 共 23 页 ,由于,则,即,从而T对乘法封闭;另一方面,当时,T关于乘法封闭,V关于乘法不封闭,故D不对,当时,T,V显然关于乘法都是封闭的,故B,C不对,故选A 例1.11变式2 解析 (1)因为,故集合不具有性质P,集合具有性质P,其相应的集合S和T是. (2)首先,由A中元素构成的有序数对 共有个,因为,所以又因为时,,所以当时,,从而集合T中元素的个数最多为,即 . 例1.11变式3 解析(1)当n=4时,,满足条件的集合A有。所以 . (2)解法一:任取偶数,则必有奇数,使得。若,则,即为偶数,为奇数;若,则,即为奇数,为偶数。所以,任意偶数是否属于集合A,完全由奇数 确定。 设集合是由集合中所有奇数组成的集合,则等于集合的子集个数,即 。 解法二:易得 , 当为奇数时,集合中满足条件的集合A有个,对于集合,考虑元素n,因为n为奇数,所以均可,故. 即,叠乘得 . 第 23 页 共 23 页 当为偶数时,集合中满足条件的集合A有个。 对于集合,考虑元素n,因为n为偶数,所以,即n是否属于集合A,完全由确定。而集合中,对于每一个满足条件的集合A,元素是否属于集合A均是确定的,故为奇数,所以 综上, . 评注:①数列的核心是递推,先从特殊的几个数(n=1,2,3,…….)入手,关键在于发现与的关系,从而发现一般规律,再给予证明。 ②递推法是处理数列问题(乃至大学学习计算机等方面)的“杀手锏”,请读者深思体会,并能灵活运用。 最有效训练题1 1.D 解析 因为,所以,故选D. 2.B 解析 因为,所以,故选B 3.A 解析 阴影部分所表示的集合为,而,故,故选A. 4.C 解析 因为,,如图1-14所示,利用数轴可得.故选C. 第 23 页 共 23 页 5. C 解析 由,即,如图1-15所示, 由图可知,所以,故选C 6. D 解析 因为,所以,又,所以.故选D 7. -1 解析 ,所以,此时,不满足集合元素的互异性,故舍去.若,同样舍去,当时,,满足题意,所以. 8.1 解析 依题意 ,所以, 从而 故A中只有三个元素, 它们的积为 . 9.解析 由,得,则 第 23 页 共 23 页 ,解得,所以的取值范围是 . 10.解析 解法一(直接法)即原方程有一个负根或两个负根,所以 ,解得,则实数的取值范围是 解法二:(间接法)设全集 } ,设方程 的两根为若方程 的根式 均非负,则 ,解得.因为,所以关于的补集即为所求. 11.解析 设 , 因为. 所以,故 .证毕 12.解析 (1)当时,集合,集合不具有性质P,因为对任意不大于10的正整数,都可以找到集合B中两元素,使得成立。 集合具有性质P, 因为可取,对于该集合中任意一对元素,都有 (2)若集合S具有性质P ,那么集合一定具有性质P . 第 23 页 共 23 页 首先因为,任取,其中,因为,所以,从而,即,所以。由S具有性质P,可知存在不大于n的正整数,使得对S中的任意一对元素,都有,对上述取定的不大于n的正整数,从集合中任取元素,其中,都有,因为,所以有,即,所以集合具有性质P 第 23 页 共 23 页查看更多