- 2021-05-12 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第6章幂函数指数函数和对数函数6
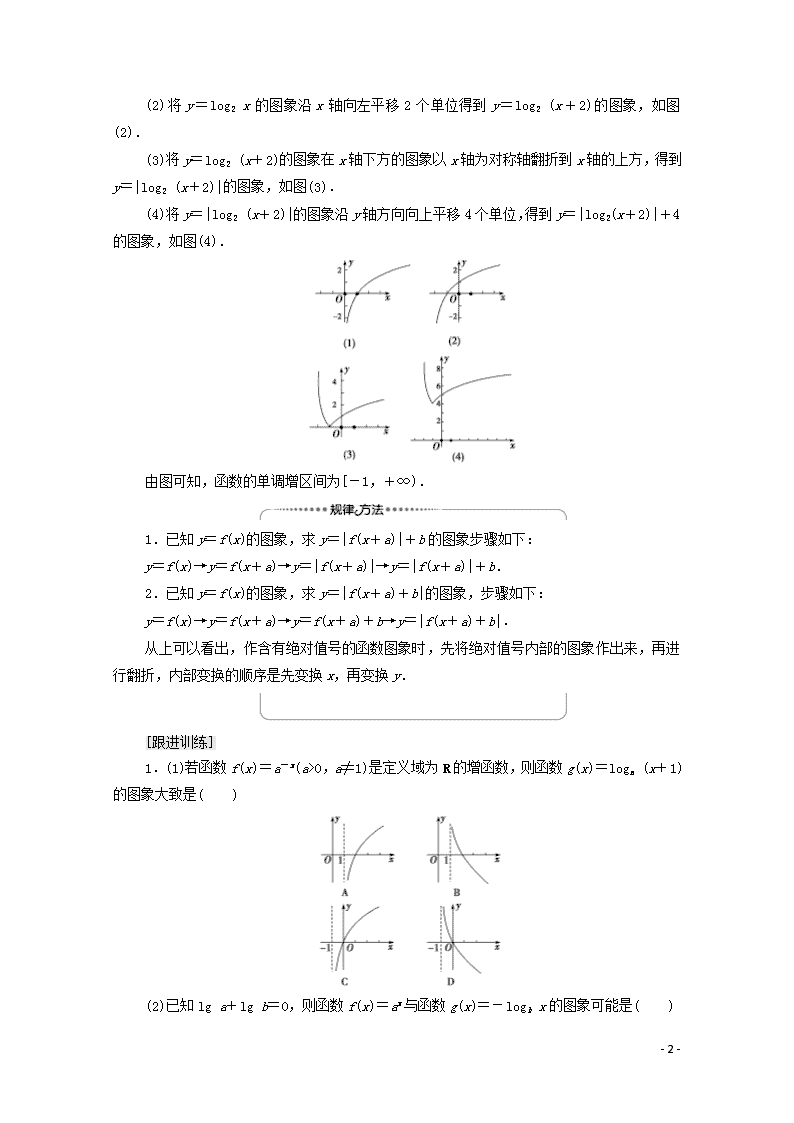
- 1 - 第 2 课时 对数函数的图象与性质的应用 学 习 目 标 核 心 素 养 1.能正确判断图象之间的变换关系.(重点) 2.理解并掌握对数函数的单调性.(重点) 3.会用对数函数的相关性质解综合题.(难点) 通过学习本节内容,提升学生的直观 想象、逻辑推理、数学运算的核心素 养. 画出对数函数 y=log2x,y=log x 的图象,说出该函数的性质,探究对数型函数 y= loga(x2-2x-3)的一般性质(定义域、值域、单调性等). 1.平移变换 当 b>0 时,将 y=logax 的图象向左平移 b 个单位,得到 y=loga(x+b)的图象;向右平 移 b 个单位,得到 y=loga(x-b)的图象.当 b>0 时,将 y=loga x 的图象向上平移 b 个单位, 得到 y=logax+b 的图象,将 y=logax 的图象向下平移 b 个单位,得到 y=logax-b 的图 象. 2.对称变换 要得到 y=loga 1 x的图象,应将 y=loga x 的图象关于 x 轴对称. 为了得到函数 y=lg x+3 10 的图象,只需把函数 y=lg x 的图象上所有的点 . 向左平移 3 个单位,再向下平移 1 个单位 [y=lg x+3 10 =lg (x+3)-1,故将 y=lgx 向左平移 3 个单位,再向下平移 1 个单位.] 对数函数的图象 【例 1】 作出函数 y=|log2 (x+2)|+4 的图象,并指出其单调增区间. [思路点拨] 可先作出 y=log2 x 的图象,再左移 2 个单位得到 y=log2 (x+2),通过翻 折变换得到 y=|log2 (x+2)|,再向上平移 4 个单位即可. [解] 步骤如下: (1)作出 y=log2 x 的图象,如图(1). (2)将 y=log2 x 的图象沿 x 轴向左平移 2 个单位得到 y=log2 (x+2)的图象,如图 - 2 - (2). (3)将 y=log2 (x+2)的图象在 x 轴下方的图象以 x 轴为对称轴翻折到 x 轴的上方,得到 y=|log2 (x+2)|的图象,如图(3). (4)将 y=|log2 (x+2)|的图象沿 y 轴方向向上平移 4 个单位,得到 y=|log2(x+2)|+4 的图象,如图(4). 由图可知,函数的单调增区间为[-1,+∞). 1.已知 y=f(x)的图象,求 y=|f(x+a)|+b 的图象步骤如下: y=f(x)→y=f(x+a)→y=|f(x+a)|→y=|f(x+a)|+b. 2.已知 y=f(x)的图象,求 y=|f(x+a)+b|的图象,步骤如下: y=f(x)→y=f(x+a)→y=f(x+a)+b→y=|f(x+a)+b|. 从上可以看出,作含有绝对值号的函数图象时,先将绝对值号内部的图象作出来,再进 行翻折,内部变换的顺序是先变换 x,再变换 y. [跟进训练] 1.(1)若函数f(x)=a-x(a>0,a≠1)是定义域为 R 的增函数,则函数 g(x)=loga (x+1) 的图象大致是( ) (2)已知 lg a+lg b=0,则函数 f(x)=ax 与函数 g(x)=-logb x 的图象可能是( ) - 3 - (1)D (2)B [(1)因为函数 f(x)=a-x 是定义域为 R 的增函数,所以 0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档