【数学】2019届一轮复习人教A版 命题及其关系、充分条件与必要条件学案
第2讲 命题及其关系、充分条件与必要条件
板块一 知识梳理·自主学习
[必备知识]
考点1 命题的概念
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
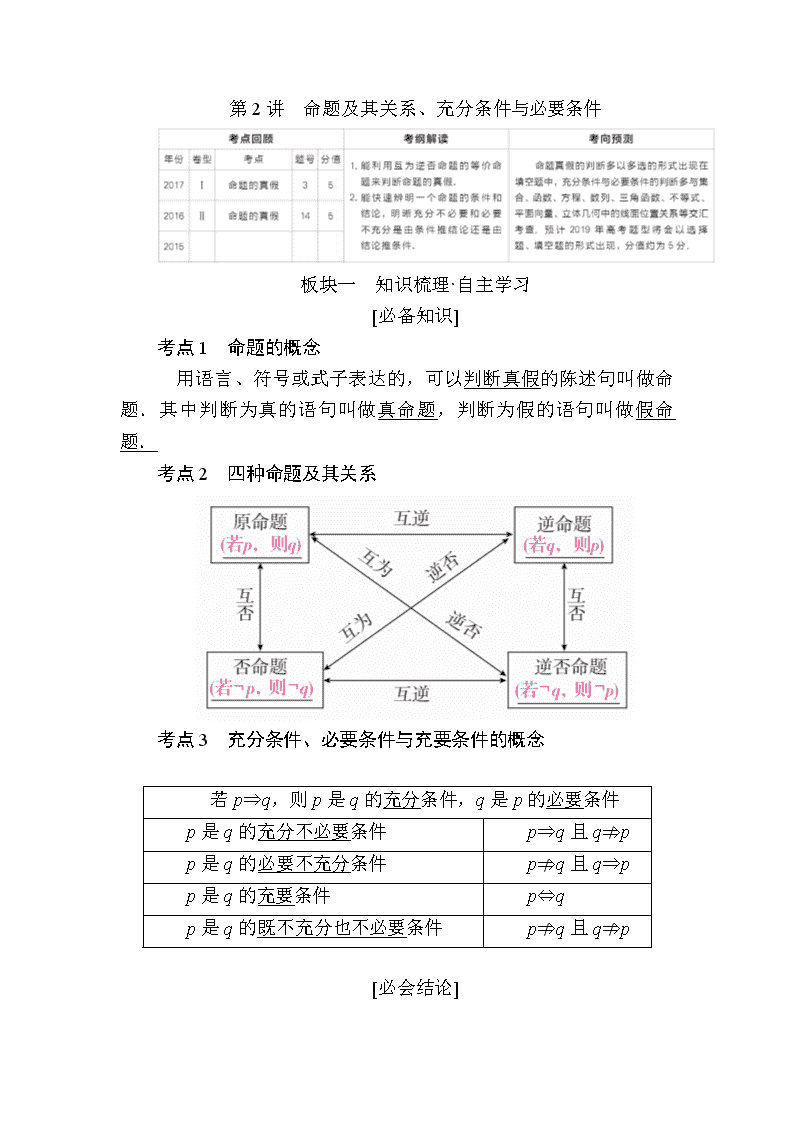
考点2 四种命题及其关系
考点3 充分条件、必要条件与充要条件的概念
若p⇒q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
p⇒q且qp
p是q的必要不充分条件
pq且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分也不必要条件
pq且qp
[必会结论]
1.两个命题互为逆否命题,它们具有相同的真假性.
2.两个命题互为逆命题或互为否命题,它们的真假性没有关系.
3.若A={x|p(x)},B={x|q(x)},则
(1)若A⊆B,则p是q的充分条件;
(2)若A⊇B,则p是q的必要条件;
(3)若A=B,则p是q的充要条件;
(4)若AB,则p是q的充分不必要条件;
(5)若AB,则p是q的必要不充分条件;
(6)若A⃘B且A⊉B,则p是q的既不充分也不必要条件.
[考点自测]
1.判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)“x2+2x-8<0”是命题.( )
(2)四种形式的命题中,真命题的个数为0或2或4.( )
(3)命题“三角形的内角和是180°”的否命题是“三角形的内角和不是180°”.( )
(4)“a=2”是“(a-1)(a-2)=0”的必要不充分条件.( )
(5)给定两个命题p,q.若p是q的充分不必要条件,则綈p是綈q的必要不充分条件.( )
答案 (1)× (2)√ (3)× (4)× (5)√
2.[课本改编]“(2x-1)x=0”是“x=0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 B
解析 若(2x-1)x=0,则x=或x=0,即不一定是x=0;若x=0,则一定能推出(2x-1)x=0.
故“(2x-1)x=0”是“x=0”的必要不充分条件.
3.[2018·安徽模拟]设p:1
1,则p是q成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案 A
解析 ∵(1,2)(0,+∞),∴p是q的充分不必要条件.
4.原命题p:“设a,b,c∈R,若a>b,则ac2>bc2”以及它的逆命题、否命题、逆否命题中,真命题的个数为( )
A.0 B.1 C.2 D.4
答案 C
解析 当c=0时,ac2=bc2,所以原命题是错误的;由于原命题与逆否命题的真假一致,所以逆否命题也是错误的;逆命题为“设a,b,c∈R,若ac2>bc2,则a>b”,它是真命题;由于否命题与逆命题的真假一致,所以逆命题与否命题都为真命题.综上所述,真命题有2个.
5.“a<0,b<0”的一个必要条件为( )
A.a+b<0 B.a-b>0
C.>1 D.<-1
答案 A
解析 若a<0,b<0,则一定有a+b<0.故选A.
6.[2018·烟台诊断]若条件p:|x|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
A.[2,+∞) B.(-∞,2]
C.[-2,+∞) D.(-∞,-2]
答案 A
解析 p:|x|≤2等价于-2≤x≤2.因为p是q的充分不必要条件,所以有[-2,2](-∞,a],即a≥2.
板块二 典例探究·考向突破
考向 四种命题及其相互关系
例 1 [2018·唐山检测]给出下列四个命题:
①“若xy=1,则x,y互为倒数”的逆命题;
②“四边相等的四边形是正方形”的否命题;
③“若a>b,则a2>b2”的逆否命题;
④“若x≤-3,则x2-x-6>0”的否命题;
其中真命题是________.(写出所有真命题的序号)
答案 ①②
解析 ①“若xy=1,则x,y互为倒数”的逆命题是“若x,y互为倒数,则xy=1”,是真命题;②“四边相等的四边形是正方形”的否命题是“四边不都相等的四边形不是正方形”,是真命题;③“若a2≤b2,则a≤b”,取a=0,b=-1,a2≤b2,但a>b,故是假命题;④“若x>-3,则x2-x-6≤0”,解不等式x2-x-6≤0可得-2≤x≤3,而x=4>-3不是不等式的解,故是假命题.
触类旁通
四种命题真假判断的方法
(1)熟悉四种命题的概念是正确书写或判断四种命题真假的关键;
(2)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假;
(3)判断一个命题为假命题可举反例.
【变式训练1】 [2017·郑州模拟]给出以下四个命题:
①“若x+y=0,则x,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤-1,则x2+x+q=0有实根”的逆否命题;
④若ab是正整数,则a,b都是正整数.
其中真命题是________.(写出所有真命题的序号)
答案 ①③
解析 ①命题“若x+y=0,则x,y互为相反数”的逆命题为“若x,y互为相反数,则x+y=0”,显然①为真命题;②不全等的三角形的面积也可能相等,故②为假命题;③原命题正确,所以它的逆否命题也正确,故③为真命题;④若ab是正整数,但a,b不一定都是正整数,例如a=-1,b=-3,故④为假命题.
考向 充分必要条件的判定
命题角度1 定义法判断充分、必要条件
例 2 [2016·四川高考]设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 若x>1且y>1,则有x+y>2成立,所以p⇒q;反之由x+
y>2不能得到x>1且y>1.所以p是q的充分不必要条件.
命题角度2 等价转化法判断充分、必要条件
例 3 给定两个命题p,q.若綈p是q的必要而不充分条件,则p是綈q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 因为綈p是q的必要不充分条件,则q⇒綈p但綈pq,其逆否命题为p⇒綈q但綈qp,所以p是綈q的充分不必要条件.
触类旁通
充分条件、必要条件的判定方法
(1)定义法:根据p⇒q,q⇒p进行判断,适用于定义、定理判断性问题.
(2)等价转化法:根据一个命题与其逆否命题的等价性,把判断的命题转化为其逆否命题进行判断,适用于条件和结论带有否定性词语的命题.
考向 充分必要条件的应用
例 4 [2018·辽宁模拟]已知命题p:|x-4|≤6,命题q:1-m≤x≤1+m,m>0,若綈p是綈q的必要而不充分条件,求实数m的取值范围.
解 p:x∈[-2,10],q:x∈[1-m,1+m],m>0.
∵綈p是綈q的必要而不充分条件,即p⇒q且qp.
∴[-2,10][1-m,1+m],
即解得m≥9,
∴实数m的取值范围是[9,+∞).
触类旁通
根据充要条件求参数的取值范围
解决此类问题一般是把充分条件、必要条件或充要条件转化为集合的包含、相等关系,然后列出有关参数的不等式(组)求解;涉及参数问题,直接解决较为困难时,可用等价转化思想,将复杂、生疏的问题转化为简单、熟悉的问题来解决,如将綈p,綈q之间的关系转化成p,q之间的关系来求解.
【变式训练2】 已知条件p:x2+2x-3>0;条件q:x>a,且綈q的一个充分不必要条件是綈p,则a的取值范围是( )
A.[1,+∞) B.(-∞,1]
C.[-1,+∞) D.(-∞,-3]
答案 A
解析 由x2+2x-3>0,得x<-3或x>1,由綈q的一个充分不必要条件是綈p,可知綈p是綈q的充分不必要条件,等价于q是p的充分不必要条件.∴{x|x>a}{x|x<-3或x>1},∴a≥1.
核心规律
判断p是q的什么条件,需要从两方面分析:一是由条件p能否推得条件q;二是由条件q能否推得条件p.
对于带有否定性的命题或比较难判断的命题,除借助集合思想把抽象、复杂问题形象化、直观化外,还可利用原命题和逆否命题、逆命题和否命题的等价性,转化为判断它的等价命题.
满分策略
1.当一个命题有大前提时,要写出其他三种命题,必须保留大前提,也就是大前提不动.
2.判断命题的真假及写四种命题时,一定要明确命题的结构,可以先把命题改写成“若p,则q”的形式.
3.判断条件之间的关系,要注意条件之间的推出方向,正确理解“p的一个充分而不必要条件是q”等语言.
板块三 启智培优·破译高考
题型技法系列1——充分必要条件的探求技巧
[2018·广东六校联考] “不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是( )
A.m> B.00 D.m>1
解题视点 有关探求充要条件的选择题,破题关键是:首先,判断是选项“推”题干,还是题干“推”选项;其次,利用以小推大的技巧,即可得结论.
解析 不等式x2-x+m>0在R上恒成立,则Δ=1-4m<0,∴m>.∴“不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是m>0.
答案 C
答题启示 注意区分以下两种不同的说法
(1)A是B的充分不必要条件,是指A⇒B但BA;
(2)A的充分不必要条件是B,是指B⇒A但AB.,以上两种说法在充要条件的推理判断中经常出现且容易混淆,在解题中一定要注意问题的设问方式,弄清它们的区别,以免出现错误判断.
跟踪训练
下面四个条件中,使a>b成立的充分而不必要的条件是( )
A.a>b+1 B.a>b-1
C.a2>b2 D.a3>b3
答案 A
解析 a>b+1⇒a>b;反之,例如a=2,b=1满足a>b,但a=b+1,即a>b推不出a>b+1,故a>b+1是a>b成立的充分而不必要的条件.故选A.
板块四 模拟演练·提能增分
[A级 基础达标]
1.[2018·江西模拟]若集合A={2,4},B={1,m2},则“A∩B={4}”是“m=2”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 B
解析 当m=2时,有A∩B={4};若A∩B={4},则m2=4,解得m=±2,不能推出m=2.故选B.
2.下列命题是真命题的为( )
A.若=,则x=y B.若x2=1,则x=1
C.若x=y,则= D.若x0”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 |x-2|<1⇔-10⇔x<-2或x>1.由于(1,3)(-∞,-2)∪(1,+∞),所以“|x-2|<1”是“x2+x-2>0”的充分而不必要条件.
4.下列结论错误的是( )
A.命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”
B.“x=4”是“x2-3x-4=0”的充分条件
C.命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题
D.命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
答案 C
解析 C项命题的逆命题为“若方程x2+x-m=0有实根,则m>0”.若方程有实根,则Δ=1+4m≥0,即m≥-,不能推出m>0,所以不是真命题.
5.[2018·长春模拟]设a,b∈R,则“(a-b)a2<0”是“a0”是“xe”是“a>b>0”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 B
解析 由e>e,得>1,解得a>b>0或ae”是“a>b>0”的必要不充分条件.
3.[2018·湖北模拟]设U为全集,A,B是集合,则“存在集合C,使得A⊆C,B⊆∁UC”是“A∩B=∅”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
答案 C
解析 因为B⊆∁UC,所以B∩C=∅.又因为A⊆C,所以A∩B=∅.
反之,若A∩B=∅,则存在集合C使得A⊆C,B⊆∁UC.
4.[2017·天津大港模拟]已知集合A=y=x2-x+1,x∈,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
解 y=x2-x+1=2+,
因为x∈,所以≤y≤2,
所以A=.
由x+m2≥1,得x≥1-m2,所以B={x|x≥1-m2}.
因为“x∈A”是“x∈B”的充分条件,所以A⊆B,
所以1-m2≤,解得m≥或m≤-,
故实数m的取值范围是∪.
5.[2018·保定模拟]已知p:x2≤5x-4,q:x2-(a+2)x+2a≤0.
(1)若p是真命题,求对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
解 (1)因为x2≤5x-4,
所以x2-5x+4≤0,
即(x-1)(x-4)≤0,所以1≤x≤4,
即对应x的取值范围为[1,4].
(2)设p对应的集合为A={x|1≤x≤4}.
由x2-(a+2)x+2a≤0,
得(x-2)(x-a)≤0.
当a=2时,不等式的解为x=2,对应的解集为B={2};
当a>2时,不等式的解为2≤x≤a,对应的解集为B={x|2≤x≤a};
当a<2时,不等式的解为a≤x≤2,对应的解集为B={x|a≤x≤2}.
若p是q的必要不充分条件,则BA,
当a=2时,满足条件;
当a>2时,因为A={x|1≤x≤4},
B={x|2≤x≤a},
要使BA,则满足2
查看更多