2008年北京市海淀区中考数学二模试卷

2008年北京市海淀区中考数学二模试卷

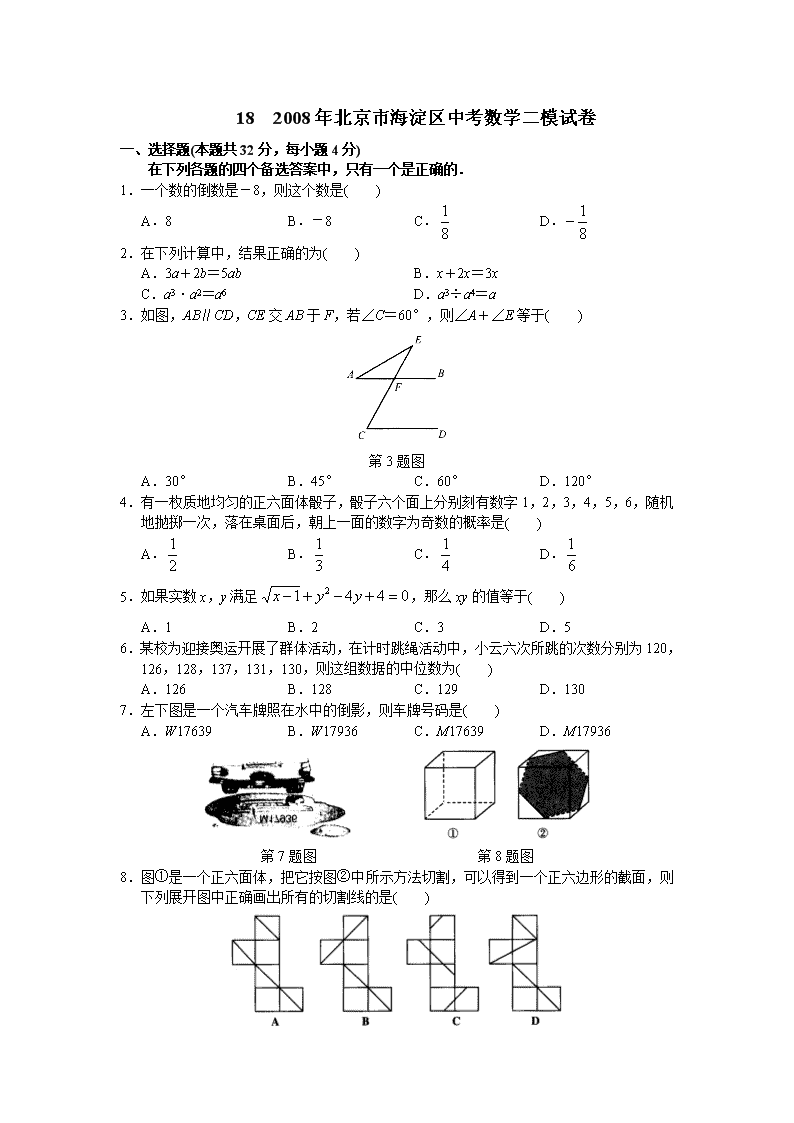
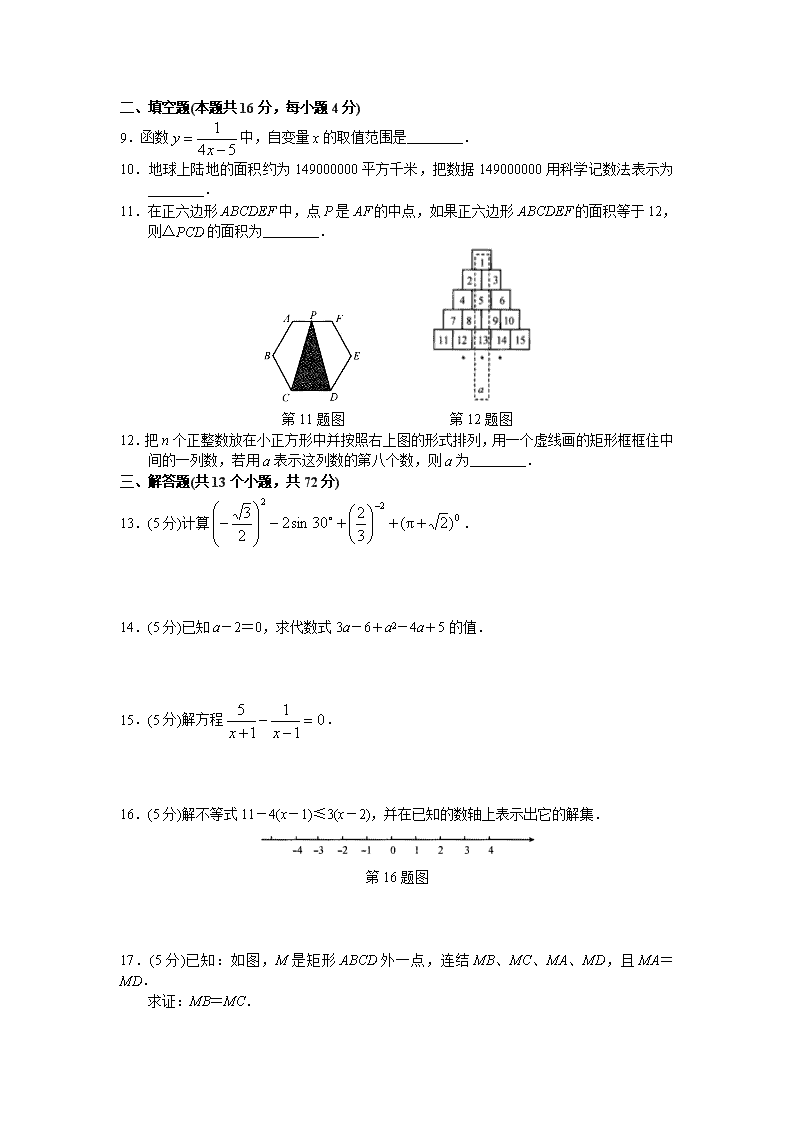
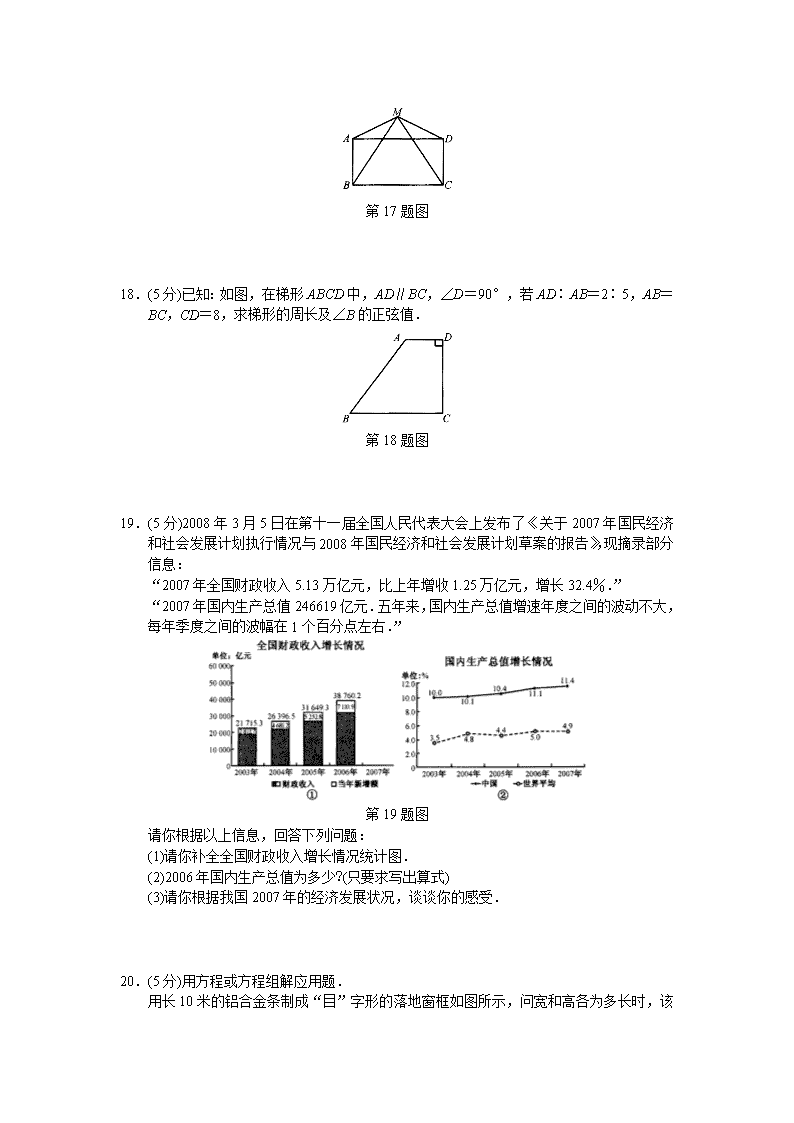
‎18 2008年北京市海淀区中考数学二模试卷 一、选择题(本题共32分，每小题4分)‎ 在下列各题的四个备选答案中，只有一个是正确的．‎ ‎1．一个数的倒数是－8，则这个数是( )‎ A．8 B．－‎8 ‎C． D．‎ ‎2．在下列计算中，结果正确的为( )‎ A．‎3a＋2b＝5ab B．x＋2x＝3x C．a3·a2＝a6 D．a3÷a4＝a ‎3．如图，AB∥CD，CE交AB于F，若∠C＝60°，则∠A＋∠E等于( )‎ 第3题图 A．30° B．45° C．60° D．120°‎ ‎4．有一枚质地均匀的正六面体骰子，骰子六个面上分别刻有数字1，2，3，4，5，6，随机地抛掷一次，落在桌面后，朝上一面的数字为奇数的概率是( )‎ A． B． C． D．‎ ‎5．如果实数x，y满足，那么xy的值等于( )‎ A．1 B．‎2 ‎C．3 D．5‎ ‎6．某校为迎接奥运开展了群体活动，在计时跳绳活动中，小云六次所跳的次数分别为120，126，128，137，131，130，则这组数据的中位数为( )‎ A．126 B．‎128 ‎C．129 D．130‎ ‎7．左下图是一个汽车牌照在水中的倒影，则车牌号码是( )‎ A．W17639 B．W‎17936 ‎C．M17639 D．M17936‎ ‎ ‎ 第7题图 第8题图 ‎8．图①是一个正六面体，把它按图②中所示方法切割，可以得到一个正六边形的截面，则下列展开图中正确画出所有的切割线的是( )‎ 二、填空题(本题共16分，每小题4分)‎ ‎9．函数中，自变量x的取值范围是________．‎ ‎10．地球上陆地的面积约为149000000平方千米，把数据149000000用科学记数法表示为________．‎ ‎11．在正六边形ABCDEF中，点P是AF的中点，如果正六边形ABCDEF的面积等于12，则△PCD的面积为________．‎ ‎ ‎ 第11题图 第12题图 ‎12．把n个正整数放在小正方形中并按照右上图的形式排列，用一个虚线画的矩形框框住中间的一列数，若用a表示这列数的第八个数，则a为________．‎ 三、解答题(共13个小题，共72分)‎ ‎13．(5分)计算．‎ ‎14．(5分)已知a－2＝0，求代数式‎3a－6＋a2－‎4a＋5的值．‎ ‎15．(5分)解方程．‎ ‎16．(5分)解不等式11－4(x－1)≤3(x－2)，并在已知的数轴上表示出它的解集．‎ 第16题图 ‎17．(5分)已知：如图，M是矩形ABCD外一点，连结MB、MC、MA、MD，且MA＝MD．‎ 求证：MB＝MC．‎ 第17题图 ‎18．(5分)已知：如图，在梯形ABCD中，AD∥BC，∠D＝90°，若AD∶AB＝2∶5，AB＝BC，CD＝8，求梯形的周长及∠B的正弦值．‎ 第18题图 ‎19．(5分)‎2008年3月5日在第十一届全国人民代表大会上发布了《关于2007年国民经济和社会发展计划执行情况与2008年国民经济和社会发展计划草案的报告》，现摘录部分信息：‎ ‎“2007年全国财政收入5.13万亿元，比上年增收1.25万亿元，增长32.4％．”‎ ‎“2007年国内生产总值246 619亿元．五年来，国内生产总值增速年度之间的波动不大，每年季度之间的波幅在1个百分点左右．”‎ 第19题图 请你根据以上信息，回答下列问题：‎ ‎(1)请你补全全国财政收入增长情况统计图．‎ ‎(2)2006年国内生产总值为多少?(只要求写出算式)‎ ‎(3)请你根据我国2007年的经济发展状况，谈谈你的感受．‎ ‎20．(5分)用方程或方程组解应用题．‎ 用长‎10米的铝合金条制成“目”‎ 字形的落地窗框如图所示，问宽和高各为多长时，该窗户的透光面积为‎3平方米(铝合金条的宽度不计)．‎ 第20题图 ‎21．(5分)已知：如图，在⊙O中，AB是弦，PF切⊙O于点B，直线PE过A点，PB＝PA．‎ ‎(1)求证：PE是⊙O的切线．‎ ‎(2)在满足(1)的情况下，当∠APB＝120°，B、C分别是⊙O的三等分点，连结CB，且PB＝2时，求弦BC的长．‎ 第21题图 ‎22．(5分)如图，已知直线y＝x＋3与x轴交于点A，与反比例函数在第一象限的图象交于点B．如果将直线AB绕点A顺时针旋转15°得到直线l，直线l与y轴交于点C．若点B的横坐标为1，求反比例函数和直线l的解析式．‎ 第22题图 ‎23．(7分)已知△ABC．‎ ‎(1)如果AB＝AC，D、E分别是AB、AC上的点，若AD＝AE，请你写出此三角形中的另一组相等的线段；‎ ‎(2)如果AB＞AC，D、E分别是AB、AC上的点，若BD＝CE，请你确定DE与BC的数量关系，并证明你的结论．‎ ‎24．(7分)已知二次函数y＝ax2＋bx＋c的图象经过点(0，3)，(3，0)，(－2，－5)．‎ ‎(1)求这个二次函数的解析式；‎ ‎(2)求这个二次函数的最值；‎ ‎(3)若设这个二次函数的图象与x轴交于点C，D(点C在点D的左侧)，且点A是该图象的顶点，请在这个二次函数图象的对称轴上确定一点B，使△ACB是等腰三角形，求出点B的坐标．‎ ‎25．(8分)根据所给的图形解答下列问题：‎ ‎(1)如图①，△ABC中，AB＝AC，∠BAC＝90°，AD⊥BC于D，把△ABD绕点A旋转，并拼接成一个与△ABC面积相等的正方形，请你在图①中完成这个作图题；‎ ‎(2)如图②，△ABC中，AB＝AC，∠BAC＝90°，请你设计一种与(1)不同的方法，将这个三角形拆分并拼接成一个与其面积相等的正方形，画出利用这个三角形得到的正方形；‎ 第25题图① 第25题图②‎ ‎(3)设计一种方法，把图③中的矩形ABCD拆分并拼接为一个与其面积相等的正方形，请你依据此矩形画出正方形，并根据你所画的图形，证明正方形的面积等于矩形ABCD的面积的结论成立．‎ 第25题图③‎ 答 案 ‎18．2008年北京市海淀区中考数学二模试卷 一、选择题 ‎1．D 2．B 3．C 4．A 5．B 6．C 7．D 8．C 二、填空题 ‎9． 10．1.49×108 11．4 12．113‎ 三、解答题 ‎13．解：原式．‎ ‎14．解法一：‎3a－6＋a2－‎4a＋5＝a2－a－1．‎ 由a－2＝0得a＝2．‎ 原式＝22－2－1＝1．‎ 解法二：‎3a－6＋a2－‎4a＋5＝3(a－2)＋(a－2)2＋1．‎ 因为a－2＝0，所以原式＝3×0＋02＋1＝1．‎ ‎15．解：5(x－1)－(x＋1)＝0． 5x－5－x－1＝0． 4x＝6． ．‎ 经检验，是原方程的解．所以原方程的解为．‎ ‎16．解：11－4x＋4≤3x－6． －7x≤－21． x≥3． 在数轴上表示其解集如下：‎ 第16题答图 ‎17．证明：在矩形ABCD中，AB＝CD，∠BAD＝∠CDA＝90°．因为△AMD中，AM＝DM，所以∠MAD＝∠MDA．所以∠MAB＝∠MDC．在△ABM和△DCM中，‎ 所以△ABM≌△DCM．所以MB＝MC．‎ ‎18．解：过A作AE⊥BC于E，‎ 则∠AEB＝∠AEC＝90°．‎ 因为AD∶AB＝2∶5，AB＝BC，‎ 所以设AD＝2k，AB＝BC＝5k(k＞0)．‎ 因为梯形ABCD中，AD∥BC，∠D＝90°，‎ 所以∠C＝180°－∠D＝90°．‎ 所以∠D＝∠C＝∠AEC＝90°．‎ 所以四边形AECD是矩形．‎ 所以AE＝CD＝8，AD＝CE＝2k．‎ 所以BE＝BC－CE＝3k．‎ 在Rt△AEB中，由勾股定理得(5k)2－(3k)2＝64．‎ 解得k＝2．‎ 所以AD＝4，AB＝BC＝10，．‎ 所以梯形ABCD的周长为32，∠B的正弦值为．‎ 第18题答图 ‎19．解：(1)补全图形如下图．‎ 第19题答图 ‎(2)(3)略．‎ ‎20．解：设宽为x米，则高为米．依题意得：．‎ 解得：x1＝1，．‎ 由x1＝1，得；由，得．‎ 故宽为‎1米，高为‎3米或宽为米，高为‎2米时，该窗户的透光面积均为‎3平方米．‎ ‎21．(1)证明：连结OA、OB、OP．因为⊙O中，AB是弦，PF切⊙O于点B，所以∠OBP＝90°．‎ 在△APO和△BPO中，‎ 所以△APO≌△BPO．所以∠OAP＝∠OBP＝90°．‎ 所以OA⊥PA．又因为OA为⊙O半径，‎ 所以PE是⊙O的切线．‎ ‎2)解：因为PA、PB是⊙O的切线，且∠APB＝120°，‎ 所以，．‎ 在Rt△OBP中，由PB＝2，‎ 得OB＝PB·tan∠OPB＝2×＝6．‎ 第21题答图 连结OC，过点O作ON⊥BC于M，交⊙O于N．‎ 所以∠COB＝120°，＝，BC＝2MB．‎ 因为的长等于⊙O的周长的三分之一，所以的长等于⊙O的周长的六分之一．‎ 所以∠MOB＝60°．在Rt△OMB中，由OB＝6，‎ 得MB＝OB·sin∠MOB＝6×＝3所以BC＝2MB＝6.‎ ‎22．解：因为点B的横坐标为1，且B点在直线y＝x＋3上，则B(1，4)．‎ 又因为B(1，4)在反比例函数(k≠0，x＞0)的图象上，‎ 所以，可得k＝4．‎ 所以反比例函数的解析式为．‎ 过B点作BD⊥x轴于D．‎ 因为直线y＝x＋3交x轴于点A，‎ 所以A(－3，0)，OA＝3．所以AD＝BD＝4．所以∠BAD＝45°．‎ 因为直线l是y＝x＋3绕点A顺时针旋转15°得到的，所以∠CAO＝30°．‎ 在Rt△AOC中，．所以C(0，)．设直线l为y＝k1x＋b(k1≠0)，‎ 由题意得解得 所以直线l的解析式为．‎ 第22题答图 ‎23．解：(1)DB＝EC．‎ ‎(2)结论：BC＞DE．‎ 证明：过E点作EF∥AB，截取EF＝DB，连结BF，‎ 作∠CEF的平分线EN，交BC于N，连结NF．‎ 因DB＝EF，DB＝EC，则EF＝EC．‎ 因EN平分∠CEF，所以∠FEN＝∠CEN．‎ 在△ENF和△ENC中，‎ 所以△ENF≌△ENC．所以NF＝NC．‎ 因为DB∥EF，DB＝EF，‎ 所以四边形BDEF是平行四边形．‎ 所以DE＝BF．‎ 在△BFN中，BN＋FN＞BF，所以BN＋CN＞DE．‎ 即BC＞DE．‎ 第23题答图①‎ 第23题答图②‎ ‎24．解：(1)因为二次函数y＝ax2＋bx＋c的图象经过点(0，3)，‎ 所以c＝3．‎ 所以二次函数的解析式为y＝ax2＋bx＋3．‎ 又因为二次函数y＝ax2＋bx＋3的图象经过点(3，0)，(－2，－5)．‎ 所以 解这个方程组得a＝－1，b＝2．‎ 所以这个二次函数的解析式为y＝－x2＋2x＋3．‎ ‎(2)因为a＝－1＜0，所以函数有最大值，当x＝1时，函数有最大值，为4．‎ ‎(3)当CA＝CB时，可求得B点的坐标为(1，－4)．‎ 当AC＝AB时，可求得B点的坐标为(1，4－2)，(1，4＋2)．‎ 当BA＝BC时，可求得B点的坐标为．‎ 综上所述，B点的坐标为(1，－4)或(1，4－2)或(1，4＋2)或．‎ 第24题答图 ‎25．解：(1)‎ 第25题答图①‎ ‎(2)图②中M、N分别是HE、GF的中点．‎ 第25题答图②‎ 第25题答图③‎ 以上给出两种方法．‎ ‎(3)设AB＝a，BC＝b．‎ 以点B为圆心，以为半径画弧，交AD于H，过C点作CE∥BH，交AD的延长线于E，过点C作CG⊥BH于G点，过E点作CE的垂线，交BH的延长线于F，则正方形EFGC为所求．‎ 证明：易证四边形EFGC是矩形，又可证△AHB∽△GBC．‎ 所以，则．可求得．‎ 因为BH∥CE，HE∥BC，‎ 所以四边形BCEH是平行四边形．‎ 所以BH＝CE．‎ 所以四边形EFGC是正方形．‎ 易证Rt△BAH≌Rt△CDE．‎ 所以S△BAH＝S△CDE．‎ 因为EF∥CG，EH∥CB，‎ 所以∠FEH＝∠GCB．‎ 因为∠EFH＝∠CGB＝90°，EF＝CG，‎ 可证△EFH≌△CGB．‎ 所以S△BCG＝S△HEF．‎ 所以S正方形EFGC＝S矩形ABCD．‎ 所以四边形EFGC为所求．‎ 第25题答图④‎