- 2021-05-12 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版(理)1-1集合及其运算学案
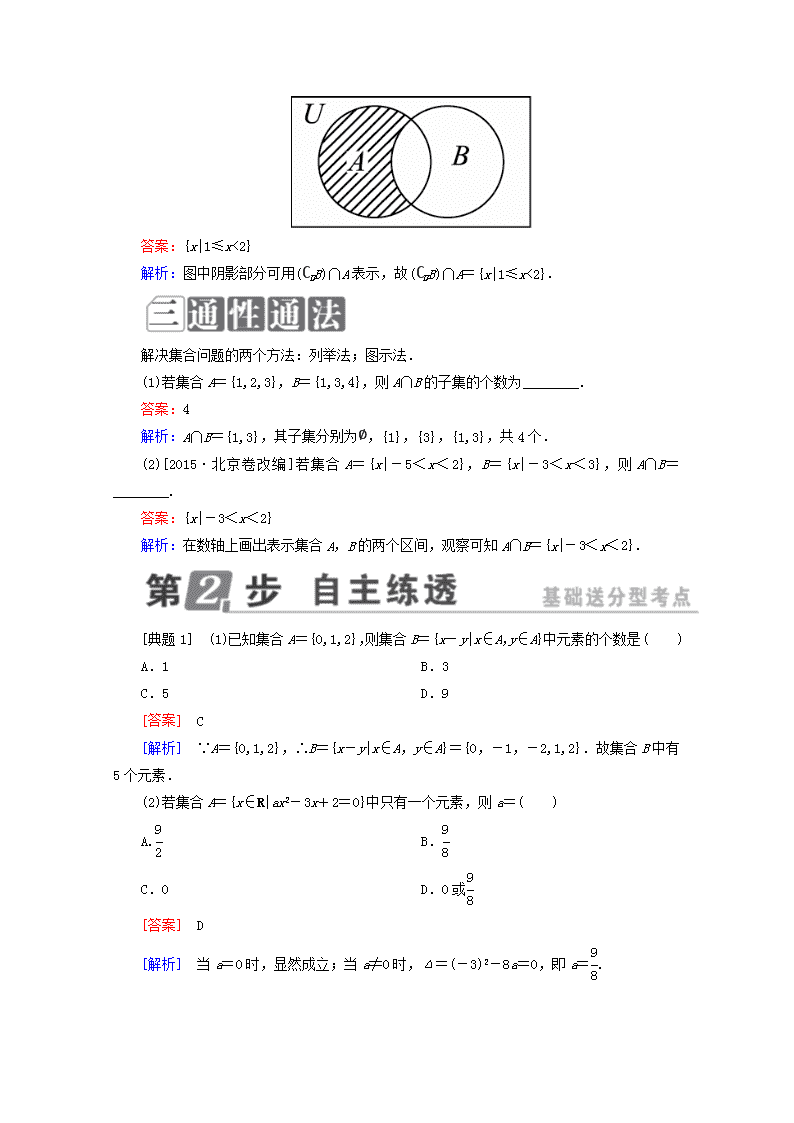
§1.1 集合及其运算 考纲展示► 1.了解集合的含义,体会元素与集合的属于关系. 2.理解集合之间包含与相等的含义,能识别给定集合的子集. 3.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集. 4.理解在给定集合中一个子集的补集的含义,会求给定子集的补集. 5.能使用韦恩(Venn)图表达集合间的基本关系及运算. 考点1 集合的基本概念 元素与集合 (1)集合元素的特性:________、________、无序性. (2)集合与元素的关系:若a属于集合A,记作________;若b不属于集合A,记作________. (3)集合的表示方法:________、________、图示法. (4)常见数集及其符号表示: 数集 自然数集 正整数集 整数集 有理数集 实数集 符号 ________ N*或N+ Z Q R 答案:(1)确定性 互异性 (2)a∈A b∉A (3)列举法 描述法 (4)N 集合表示的两个误区:集合的代表元素;图示法. (1)已知集合A={y|y=sin x},B={x|y=sin x},则A∩B=________. 答案:[-1,1] 解析:集合A表示的是函数y=sin x的值域,即A=[-1,1];集合B表示的是函数y=sin x的定义域,即B=R,所以A∩B=[-1,1]. (2)设全集U=R,A={x|0<x<2},B={x|x<1},则图中阴影部分表示的集合为________. 答案:{x|1≤x<2} 解析:图中阴影部分可用(∁UB)∩A表示,故(∁UB)∩A={x|1≤x<2}. 解决集合问题的两个方法:列举法;图示法. (1)若集合A={1,2,3},B={1,3,4},则A∩B的子集的个数为________. 答案:4 解析:A∩B={1,3},其子集分别为∅,{1},{3},{1,3},共4个. (2)[2015·北京卷改编]若集合A={x|-5<x<2},B={x|-3<x<3},则A∩B=________. 答案:{x|-3<x<2} 解析:在数轴上画出表示集合A,B的两个区间,观察可知A∩B={x|-3<x<2}. [典题1] (1)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( ) A.1 B.3 C.5 D.9 [答案] C [解析] ∵A={0,1,2},∴B={x-y|x∈A,y∈A}={0,-1,-2,1,2}.故集合B中有5个元素. (2)若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=( ) A. B. C.0 D.0或 [答案] D [解析] 当a=0时,显然成立;当a≠0时,Δ=(-3)2-8a=0,即a=. (3)设a,b∈R,集合{1,a+b,a}=,则b-a=( ) A.1 B.-1 C.2 D.-2 [答案] C [解析] 因为{1,a+b,a}=,a≠0, 所以a+b=0,则=-1, 所以a=-1,b=1,所以b-a=2. (4)已知集合A={m+2,2m2+m},若3∈A,则m的值为________. [答案] - [解析] 由题意得m+2=3或2m2+m=3,则m=1或m=-.当m=1时,m+2=3且2m2+m=3,根据集合中元素的互异性可知不满足题意;当m=-时,m+2=,而2m2+m=3,故m=-. [点石成金] 与集合中的元素有关问题的求解策略 (1)用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型集合. (2)集合中元素的三个特性中的互异性对解题的影响较大,特别是含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性. 考点2 集合间的基本关系 集合间的基本关系 表示 关系 文字语言 记法 集合 间的 基本 子集 集合A中任意一个元素都是集合B中的元素 __________或__________ 关系 真子集 集合A是集合B的子集,并且B __________或__________ 中至少有一个元素不属于A 相等 集合A的每一个元素都是集合B的元素,集合B的每一个元素也都是集合A的元素 A⊆B且B⊆A⇔A=B 空集 空集是________集合的子集 ∅⊆A 空集是________集合的真子集 ∅B且B≠∅ 答案:A⊆B B⊇A AB BA 任何 任何非空 集合中的两个易混结论:集合中元素的个数;集合的子集的个数. (1)[2015·江苏卷]已知集合A={1,2,3},B={2,4,5},则集合A∪B中元素的个数为________. 答案:5 解析:因为A∪B={1,2,3,4,5},所以A∪B中元素的个数为5. (2)集合A={1,4,7,10,13,16,19,21},则集合A有________个子集、________个真子集、________个非空子集、________个非空真子集. 答案:28 28-1 28-1 28-2 解析:因为集合A中有8个元素,所以集合A有28个子集,28-1个真子集,28-1个非空子集,28-2个非空真子集. [典题2] (1)设P={y|y=-x2+1,x∈R},Q={y|y=2x,x∈R},则( ) A.P⊆Q B.Q⊆P C.∁RP⊆Q D.Q⊆∁RP [答案] C [解析] 因为P={y|y=-x2+1,x∈R}={y|y≤1},Q={y|y=2x,x∈R}={y|y>0},所以∁RP={y|y>1},所以∁RP⊆Q,故选C. (2)已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为( ) A.1 B.2 C.3 D.4 [答案] D [解析] 由x2-3x+2=0得x=1或x=2, ∴A={1,2}. 由题意知B={1,2,3,4}, ∴满足条件的C可为{1,2},{1,2,3},{1,2,4},{1,2,3,4}. (3)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B⊆A,则实数m的取值范围为________. [答案] (-∞,3] [解析] ∵B⊆A, ∴①若B=∅,则2m-1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档