- 2021-05-12 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学第二轮专题复习专题三
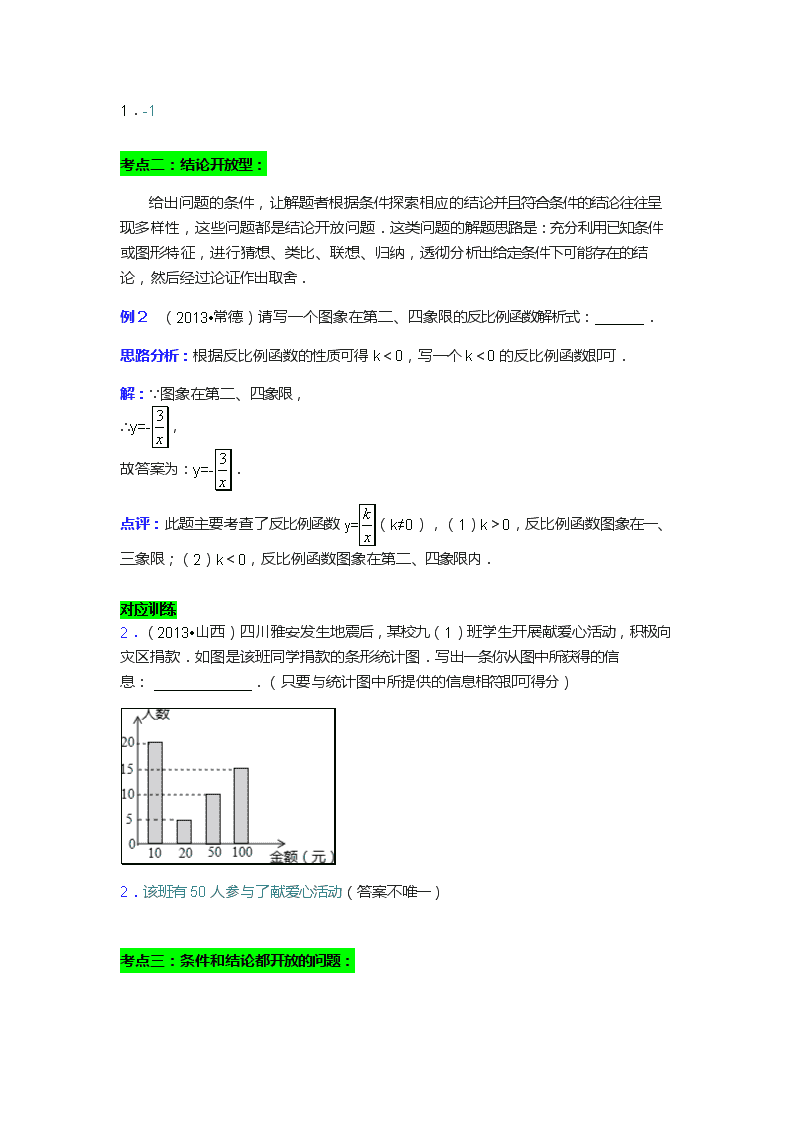
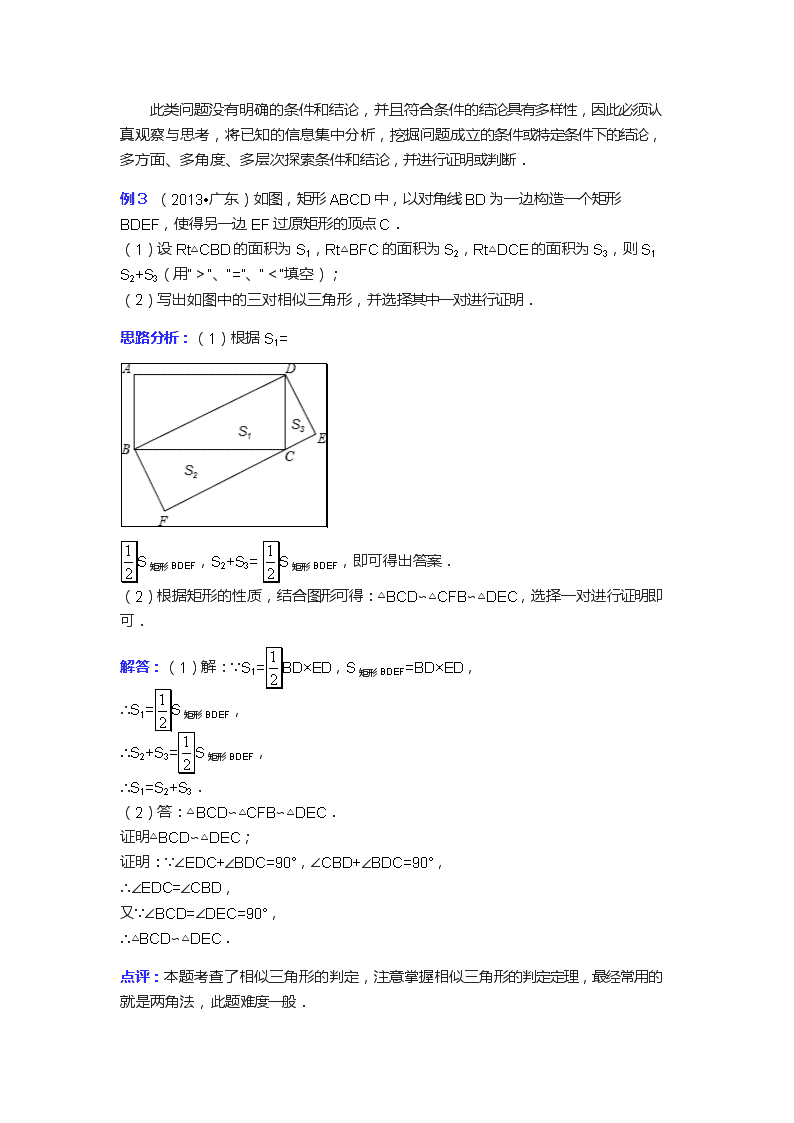
专题三 开放型问题 一、中考专题诠释 开放型问题是相对于有明确条件和明确结论的封闭型问题而言的,它是条件或结论给定不完全、答案不唯一的一类问题.这类试题已成为近年中考的热点,重在考查同学们分析、探索能力以及思维的发散性,但难度适中.根据其特征大致可分为:条件开放型、结论开放型、方法开放型和编制开放型等四类. 二、解题策略与解法精讲 解开放性的题目时,要先进行观察、试验、类比、归纳、猜测出结论或条件,然后严格证明;同时,通常要结合以下数学思想方法:分类讨论,数形结合,分析综合,归纳猜想,构建数学模型等。 三、中考考点精讲 考点一:条件开放型 条件开放题是指结论给定,条件未知或不全,需探求与结论相对应的条件.解这种开放问题的一般思路是:由已知的结论反思题目应具备怎样的条件,即从题目的结论出发,逆向追索,逐步探求. 例1 (2013•盐城)写出一个过点(0,3),且函数值y随自变量x的增大而减小的一次函数关系式: y=-x+3 .(填上一个答案即可) 思路分析:首先可以用待定系数法设此一次函数关系式是:y=kx+b(k≠0).根据已知条件确定k,b应满足的关系式,再根据条件进行分析即可. 解:设此一次函数关系式是:y=kx+b. 把x=0,y=3代入得:b=3, 又根据y随x的增大而减小,知:k<0. 故此题只要给定k一个负数,代入解出b值即可.如y=-x+3.(答案不唯一) 故答案是:y=-x+3. 点评:本题考查了一次函数的性质.掌握待定系数法,首先根据已知条件确定k,b应满足的关系式,再根据条件进行分析即可. 对应训练 1.(2013•达州)已知(x1,y1),(x2,y2)为反比例函数图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 -1 .(只需写出符合条件的一个k的值) 1.-1 考点二:结论开放型: 给出问题的条件,让解题者根据条件探索相应的结论并且符合条件的结论往往呈现多样性,这些问题都是结论开放问题.这类问题的解题思路是:充分利用已知条件或图形特征,进行猜想、类比、联想、归纳,透彻分析出给定条件下可能存在的结论,然后经过论证作出取舍. 例2 (2013•常德)请写一个图象在第二、四象限的反比例函数解析式: . 思路分析:根据反比例函数的性质可得k<0,写一个k<0的反比例函数即可. 解:∵图象在第二、四象限, ∴y=-, 故答案为:y=-. 点评:此题主要考查了反比例函数y=(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内. 对应训练 2.(2013•山西)四川雅安发生地震后,某校九(1)班学生开展献爱心活动,积极向灾区捐款.如图是该班同学捐款的条形统计图.写出一条你从图中所获得的信息: 该班有50人参与了献爱心活动 .(只要与统计图中所提供的信息相符即可得分) 2.该班有50人参与了献爱心活动(答案不唯一) 考点三:条件和结论都开放的问题: 此类问题没有明确的条件和结论,并且符合条件的结论具有多样性,因此必须认真观察与思考,将已知的信息集中分析,挖掘问题成立的条件或特定条件下的结论,多方面、多角度、多层次探索条件和结论,并进行证明或判断. 例3 (2013•广东)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C. (1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 = S2+S3(用“>”、“=”、“<”填空); (2)写出如图中的三对相似三角形,并选择其中一对进行证明. 思路分析:(1)根据S1= S矩形BDEF,S2+S3= S矩形BDEF,即可得出答案. (2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可. 解答:(1)解:∵S1=BD×ED,S矩形BDEF=BD×ED, ∴S1=S矩形BDEF, ∴S2+S3=S矩形BDEF, ∴S1=S2+S3. (2)答:△BCD∽△CFB∽△DEC. 证明△BCD∽△DEC; 证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°, ∴∠EDC=∠CBD, 又∵∠BCD=∠DEC=90°, ∴△BCD∽△DEC. 点评:本题考查了相似三角形的判定,注意掌握相似三角形的判定定理,最经常用的就是两角法,此题难度一般. 对应训练 3.(2013•荆州)如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连结BE.请找出一对全等三角形,并说明理由. 3.解:△ACD≌△BCE. 证明如下∵∠ACB=∠DCE=90°, ∴∠ACB-∠DCB=∠DCE-∠DCB, 即∠ACD=∠BCE. ∵△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°, ∴CA=CB,CD=CE, 在△ACD和△BCE中, , ∴△ACD≌△BCE.查看更多