- 2021-05-12 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习(理)专题65数学归纳法学案(全国通用)
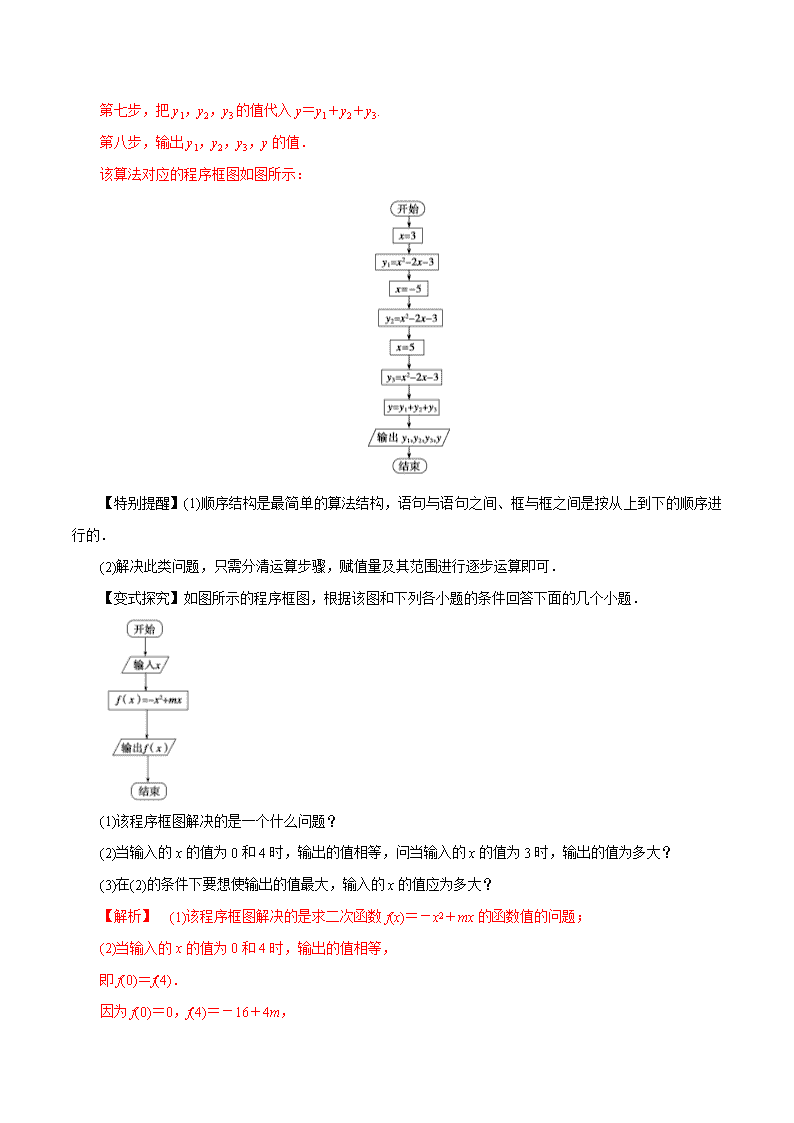
1.了解数学归纳法的原理; 2.能用数学归纳法证明一些简单的数学命题。 1.数学归纳法 证明一个与正整数n有关的命题,可按下列步骤进行: (1)(归纳奠基)证明当n取第一个值n0(n0∈N )时命题成立; (2)(归纳递推)假设n=k(k≥n0,k∈N )时命题成立,证明当n=k+1时命题也成立. 只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立. 2.数学归纳法的框图表示 高频考点一 算法的顺序结构 例1、f(x)=x2-2x-3.求f(3)、f(-5)、f(5),并计算f(3)+f(-5)+f(5)的值.设计出解决该问题的一个算法,并画出程序框图. 第六步,把x=5代入y3=x2-2x-3. 第七步,把y1,y2,y3的值代入y=y1+y2+y3. 第八步,输出y1,y2,y3,y的值. 该算法对应的程序框图如图所示: 【特别提醒】(1)顺序结构是最简单的算法结构,语句与语句之间、框与框之间是按从上到下的顺序进行的. (2)解决此类问题,只需分清运算步骤,赋值量及其范围进行逐步运算即可. 【变式探究】如图所示的程序框图,根据该图和下列各小题的条件回答下面的几个小题. (1)该程序框图解决的是一个什么问题? (2)当输入的x的值为0和4时,输出的值相等,问当输入的x的值为3时,输出的值为多大? (3)在(2)的条件下要想使输出的值最大,输入的x的值应为多大? 【解析】 (1)该程序框图解决的是求二次函数f(x)=-x2+mx的函数值的问题; (2)当输入的x的值为0和4时,输出的值相等, 即f(0)=f(4). 因为f(0)=0,f(4)=-16+4m, 所以-16+4m=0, 所以m=4,f(x)=-x2+4x. 则f(3)=-32+4×3=3, 所以当输入的x的值为3时,输出的f(x)的值为3; 高频考点二 算法的条件结构 例2、如图中x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分.当x1=6,x2=9,p=8.5时,x3等于( ) A.11B.10C.8D.7 思维点拨 依据第二个判断框的条件关系,判断是利用“x2=x3”,还是利用“x1=x3”,从而验证p是否为8.5. 【答案】C 【解析】x1=6,x2=9,|x1-x2|=3<2不成立,即为“否”,所以再输入x3;由绝对值的意义(一个点到另一个点的距离)和不等式|x3-x1|<|x3-x2|知,点x3到点x1的距离小于点x3到点x2的距离,所以当x3<7.5时,|x3-x1|<|x3-x2|成立,即为“是”,此时x2=x3,所以p=,即=8.5,解得x3=11>7.5,不合题意;当x3>7.5时,|x3-x1|<|x3-x2|不成立,即为“否”,此时x1=x3,所以p=,即=8.5,解得x3=8>7.5,符合题意,故选C. 【特别提醒】 (1)条件结构中条件的判断关键是明确条件结构的功能,然后根据“是”的分支成立的条件进行判断; (2)对条件结构,无论判断框中的条件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支. 【变式探究】(2014·四川)执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为( ) A.0 B.1 C.2 D.3 【答案】C 【解析】当条件x≥0,y≥0,x+y≤1不成立时输出S的值为1;当条件x≥0,y≥0,x+y≤1成立时S=2x+y,下面用线性规划的方法求此时S的最大值. 高频考点三 算法的循环结构 例3、执行如图所示的程序框图,则输出s的值为( ) A.10 B.17 C.19 D.36 【答案】C 【特别提醒】 利用循环结构表示算法,第一要确定是利用当型还是直到型循环结构;第二准确表示累计变量;第三要注意从哪一步开始循环.弄清进入或终止的循环条件、循环次数是做题的关键. 【变式探究】当m=7,n=3时,执行如图所示的程序框图,输出的S值为( ) A.7B.42C.210D.840 【答案】C 【解析】程序框图的执行过程如下: m=7,n=3时,m-n+1=5, k=m=7,S=1,S=1×7=7; k=k-1=6>5,S=6×7=42; k=k-1=5=5,S=5×42=210; k=k-1=4<5,输出S=210.故选C. 高频考点四 基本算法语句 例4、阅读下面两个算法语句: 图1 图2 执行图1中语句的结果是输出 ; 执行图2中语句的结果是输出 . 【答案】i=4 i=2 【特别提醒】解决算法语句有三个步骤:首先通读全部语句,把它翻译成数学问题;其次领悟该语句的功能;最后根据语句的功能运行程序,解决问题. 【变式探究】 设计一个计算1×3×5×7×9×11×13的算法.图中给出了程序的一部分,则在横线上不能填入的数是( ) A.13 B.13.5 C.14 D.14.5 【答案】A 1.【2016江苏高考,26】(1)求的值; (2)设m,nN ,n≥m,求证: (m+1)+(m+2)+(m+3)++n+(n+1)=(m+1). 【答案】(1)0(2)详见解析 【解析】(1) (2)当时,结论显然成立,当时 又因为 所以 因此 1.【2015江苏高考,23】(本小题满分10分) 已知集合,, ,令表示集合所含元素的个数. (1)写出的值; (2)当时,写出的表达式,并用数学归纳法证明. 【答案】(1)13(2) 【解析】(1). (2)当时,(). 下面用数学归纳法证明: ①当时,,结论成立; ②假设()时结论成立,那么时,在的基础上新增加的元素在,,中产生,分以下情形讨论: 4)若,则,此时有 ,结论成立; 5)若,则,此时有 ,结论成立; 6)若,则,此时有 ,结论成立.学 综上所述,结论对满足的自然数均成立. 2.【2015高考北京,理20】已知数列满足:,,且. 记集合. (Ⅰ)若,写出集合的所有元素; (Ⅱ)若集合存在一个元素是3的倍数,证明:的所有元素都是3的倍数; (Ⅲ)求集合的元素个数的最大值. 【答案】(1),(2)证明见解析,(3)8 【解析】(Ⅰ)由已知可知: (Ⅱ)因为集合存在一个元素是3的倍数,所以不妨设是3的倍数,由已知,可用用数学归纳法证明对任意,是3的倍数,当时,则M中的所有元素都是3的倍数,如果时,因为或,所以是3的倍数,于是是3的倍数,类似可得,都是3的倍数,从而对任意,是3的倍数,因此的所有元素都是3的倍数. ②中没有3的倍数,则都不是3的倍数,对于除以9的余数只能是1,4,7,2,5,8中的一个,从起,除以9的余数是1,2,4,8,7,5,1,2,4,8, ,不断的6项循环(可能从2,4,8,7或5开始),而除以9的余数是1,2,4,8,5且是4的倍数(不大于36),只有28,20,4,8,16,32,所以M中的项加上前两项最多8项,则时,,项数为8,所以集合的元素个数的最大值为8. 3.(2014·安徽卷) 设实数c>0,整数p>1,n∈N . (1)证明:当x>-1且x≠0时,(1+x)p>1+px; (2)数列{an}满足a1>c,an+1=an+a,证明:an>an+1>c. (2)方法一:先用数学归纳法证明an>c. ①当n=1时,由题设知a1>c成立. ②假设n=k(k≥1,k∈N )时,不等式ak>c成立. 由an+1=an+a易知an>0,n∈N . 当n=k+1时,=+a= 1+. 由ak>c>0得-1<-<<0. 由(1)中的结论得=>1+p· =. 因此a>c,即ak+1>c, 所以当n=k+1时,不等式an>c也成立. 综合①②可得,对一切正整数n,不等式an>c均成立. 再由=1+可得<1, 即an+1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档