2020届二轮复习选择题、填空题综合练(二)作业

2020届二轮复习选择题、填空题综合练(二)作业

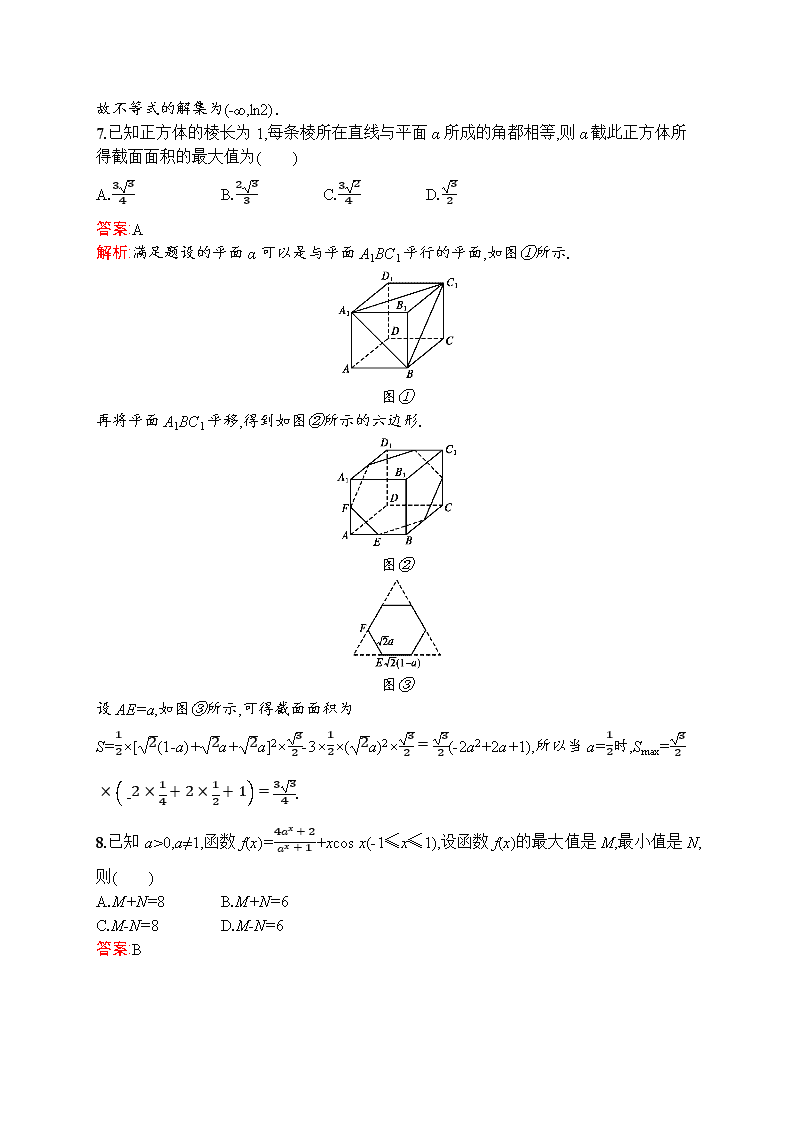
题型练2　选择题、填空题综合练(二)‎ ‎　题型练第52页　 ‎ 一、能力突破训练 ‎1.已知全集U={1,2,3,4,5},A={1,3},则∁UA=(　　)‎ A.⌀ B.{1,3} ‎ C.{2,4,5} D.{1,2,3,4,5}‎ 答案:C 解析:∵A={1,3},U={1,2,3,4,5},‎ ‎∴∁UA={2,4,5},故选C.‎ ‎2.(2019甘肃、青海、宁夏3月联考)如图,某瓷器菜盘的外轮廓线是椭圆,根据图中数据可知该椭圆的离心率为(　　)‎ A.‎2‎‎5‎ B.‎3‎‎5‎ C.‎2‎‎3‎‎5‎ D.‎‎2‎‎5‎‎5‎ 答案:B 解析:由题意知2b=16.4,2a=20.5,则ba‎=‎‎4‎‎5‎,则离心率e=‎1-‎‎4‎‎5‎‎2‎‎=‎‎3‎‎5‎.故选B.‎ ‎3.已知sin θ=m-3‎m+5‎,cos θ=‎4-2mm+5‎π‎2‎‎<θ<π,则tanθ‎2‎等于(　　)‎ A.m-3‎‎9-m B.‎m-3‎‎|9-m|‎ C.‎1‎‎3‎ D.5‎ 答案:D 解析:利用同角正弦、余弦的平方和为1求m的值,再根据半角公式求tanθ‎2‎,但运算较复杂,试根据答案的数值特征分析.由于受条件sin2θ+cos2θ=1的制约,m为一确定的值,进而推知tanθ‎2‎也为一确定的值,又π‎2‎<θ<π,所以π‎4‎‎<θ‎2‎<‎π‎2‎,故tanθ‎2‎>1.‎ ‎4.将函数f(x)=2sin x图象上各点的横坐标缩短到原来的‎1‎‎2‎,纵坐标不变,然后向左平移π‎6‎个单位长度,得到函数y=g(x)的图象.若关于x的方程g(x)=a在区间‎-π‎4‎,‎π‎4‎上有两个不相等的实根,则实数a的取值范围是(　　)‎ A.[-2,2] B.[-2,2) C.[1,2) D.[-1,2)‎ 答案:C 解析:将函数f(x)=2sinx图象上各点的横坐标缩短到原来的‎1‎‎2‎,纵坐标不变,得到y=2sin2x的图象,然后将其向左平移π‎6‎个单位长度,得到g(x)=2sin‎2‎x+‎π‎6‎=2sin‎2x+‎π‎3‎的图象.‎ 因为-π‎4‎≤x≤π‎4‎,所以-π‎6‎≤2x+π‎3‎‎≤‎‎5π‎6‎,‎ 所以当2x+π‎3‎‎=‎‎5π‎6‎时,g(x)=2sin‎5π‎6‎=2×‎1‎‎2‎=1;‎ 当2x+π‎3‎‎=‎π‎2‎时,g(x)max=2.‎ 因为关于x的方程g(x)=a在区间‎-π‎4‎,‎π‎4‎上有两个不相等的实根,所以1≤a<2.‎ 故实数a的取值范围是[1,2),故选C.‎ ‎5.已知等差数列{an}的通项是an=1-2n,前n项和为Sn,则数列Snn的前11项和为(　　)‎ A.-45 B.-50 C.-55 D.-66‎ 答案:D 解析:由an=1-2n,a1=-1,Sn=n(-1+1-2n)‎‎2‎=-n2,Snn=-n,所以数列Snn的前11项和为‎11×(-1-11)‎‎2‎=-66.故选D.‎ ‎6.定义在(0,+∞)上的函数f(x)满足x2f'(x)>1,f(2)=‎5‎‎2‎,则关于x的不等式f(ex)<3-‎1‎ex的解集为(　　)‎ A.(0,e2) B.(e2,+∞) ‎ C.(0,ln 2) D.(-∞,ln 2)‎ 答案:D 解析:构造函数F(x)=f(x)+‎1‎x,依题意可知F'(x)=f'(x)-‎1‎x‎2‎‎=‎x‎2‎f'(x)-1‎x‎2‎>0,即函数f(x)在(0,+∞)上单调递增,所求不等式可化为F(ex)=f(ex)+‎1‎ex<3,而F(2)=f(2)+‎1‎‎2‎=3,所以ex<2,解得x0,a≠1,函数f(x)=‎4ax+2‎ax‎+1‎+xcos x(-1≤x≤1),设函数f(x)的最大值是M,最小值是N,则(　　)‎ A.M+N=8 B.M+N=6‎ C.M-N=8 D.M-N=6‎ 答案:B 解析:f(x)=‎4ax+2‎ax‎+1‎+xcosx=3+ax‎-1‎ax‎+1‎+xcosx.设g(x)=ax‎-1‎ax‎+1‎+xcosx,则g(-x)=-g(x),函数g(x)是奇函数,则g(x)的值域为关于原点对称的区间,当-1≤x≤1时,设-m≤g(x)≤m(m≥0),则3-m≤f(x)≤3+m,‎ ‎∴函数f(x)的最大值M=3+m,最小值N=3-m,得M+N=6,故选B.‎ ‎9.已知‎(1-i‎)‎‎2‎z=1+i(i为虚数单位),则复数z=　　　　　. ‎ 答案:-1-i 解析:由已知得z=‎(1-i‎)‎‎2‎‎1+i‎=‎-2i‎1+i=‎-2i(1-i)‎‎(1+i)(1-i)‎=‎‎-2-2i‎2‎=-1-i.‎ ‎10.若a,b∈R,ab>0,则a‎4‎‎+4b‎4‎+1‎ab的最小值为　　　　　. ‎ 答案:4‎ 解析:∵a,b∈R,且ab>0,‎ ‎∴a‎4‎‎+4b‎4‎+1‎ab‎≥‎‎4a‎2‎b‎2‎+1‎ab=4ab+‎1‎ab≥4当且仅当a‎2‎‎=2b‎2‎,‎‎4ab=‎1‎ab,‎即a‎2‎‎=‎2‎‎2‎,‎b‎2‎‎=‎‎2‎‎4‎时取等号.‎ ‎11.已知f(x)为偶函数,当x<0时,f(x)=ln(-x)+3x,则曲线y=f(x)在点(1,-3)处的切线方程是　　　　　　　　　　. ‎ 答案:y=-2x-1‎ 解析:当x>0时,-x<0,‎ 则f(-x)=lnx-3x.‎ 因为f(x)为偶函数,所以f(x)=f(-x)=lnx-3x,所以f'(x)=‎1‎x-3,f'(1)=-2.‎ 故所求切线方程为y+3=-2(x-1),‎ 即y=-2x-1.‎ ‎12.已知点B(x0,2)在曲线y=2sin ωx(ω>0)上,T是y=2sin ωx的最小正周期.若点A(1,0),OA‎·‎OB=1,且00)上,‎ ‎∴sinω=1,即ω=π‎2‎+2kπ,k∈N.‎ 又T>1,即‎2πω>1,∴2π>π‎2‎+2kπ,即k<‎3‎‎4‎.‎ ‎∵k∈N,∴k=0,∴ω=π‎2‎,‎ 即T=‎2πω=4.‎ ‎13.已知直线y=mx与函数f(x)=‎2-‎1‎‎3‎x,x≤0,‎‎1‎‎2‎x‎2‎‎+1,x>0‎的图象恰好有三个不同的公共点,则实数m的取值范围是　　　　　. ‎ 答案:(‎2‎,+∞)‎ 解析:作出函数f(x)=‎2-‎1‎‎3‎x,x≤0,‎‎1‎‎2‎x‎2‎‎+1,x>0‎的图象,如图.‎ 直线y=mx的图象是绕坐标原点旋转的动直线.当斜率m≤0时,直线y=mx与函数f(x)的图象只有一个公共点;当m>0时,直线y=mx始终与函数y=2-‎1‎‎3‎x(x≤0)的图象有一个公共点,故要使直线y=mx与函数f(x)的图象有三个公共点,必须使直线y=mx与函数y=‎1‎‎2‎x2+1(x>0)的图象有两个公共点,即关于x的方程mx=‎1‎‎2‎x2+1在x>0时有两个不相等的实数根,即关于x的方程x2-2mx+2=0的判别式Δ=4m2-4×2>0,解得m>‎2‎.故所求实数m的取值范围是(‎2‎,+∞).‎ 二、思维提升训练 ‎14.复数z=‎2+ii(i为虚数单位)的虚部为(　　)‎ A.2 B.-2 C.1 D.-1‎ 答案:B 解析:∵z=‎2+ii‎=‎‎(2+i)ii‎2‎=1-2i,∴复数z的虚部为-2,故选B.‎ ‎15.已知a=‎2‎‎4‎‎3‎,b=‎4‎‎2‎‎5‎,c=2‎5‎‎1‎‎3‎,则(　　)‎ A.b‎‎4‎‎2‎‎5‎=b,c=2‎5‎‎1‎‎3‎‎=‎5‎‎2‎‎3‎>‎‎4‎‎2‎‎3‎=a,‎ 所以b0,|φ|<‎π‎2‎的部分图象如图所示,则该简谐运动的最小正周期T和初相φ分别为(　　)‎ A.T=6π,φ=‎π‎6‎ B.T=6π,φ=‎π‎3‎ C.T=6,φ=‎π‎6‎ D.T=6,φ=‎π‎3‎ 答案:C 解析:由题图可知A=2,T=6,∴ω=π‎3‎.‎ ‎∵图象过点(1,2),∴sinπ‎3‎‎×1+φ=1,‎ ‎∴φ+π‎3‎=2kπ+π‎2‎,k∈Z,又|φ|<π‎2‎,∴φ=π‎6‎.‎ ‎18.如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD上的动点,则AE‎·‎BE的最小值为(　　)‎ A.‎21‎‎16‎ B.‎‎3‎‎2‎ C.‎25‎‎16‎ D.3‎ 答案:A 解析:如图,取AB的中点F,连接EF.‎ AE‎·‎BE ‎=‎‎(AE+BE‎)‎‎2‎-(AE-‎BE‎)‎‎2‎‎4‎ ‎=‎(2FE‎)‎‎2‎-‎AB‎2‎‎4‎=|FE|2-‎1‎‎4‎.‎ 当EF⊥CD时,|EF|最小,即AE‎·‎BE取最小值.‎ 过点A作AH⊥EF于点H.由AD⊥CD,EF⊥CD,可得EH=AD=1,∠DAH=90°.‎ 因为∠DAB=120°,所以∠HAF=30°.‎ 在Rt△AFH中,易知AF=‎1‎‎2‎,HF=‎1‎‎4‎,‎ 所以EF=EH+HF=1+‎1‎‎4‎‎=‎‎5‎‎4‎.‎ 所以(AE‎·‎BE)min=‎5‎‎4‎‎2‎‎-‎1‎‎4‎=‎‎21‎‎16‎.‎ ‎19.在△ABC中,AC=‎7‎,BC=2,B=60°,则BC边上的高等于(　　)‎ A.‎3‎‎2‎ B.‎‎3‎‎3‎‎2‎ C.‎3‎‎+‎‎6‎‎2‎ D.‎‎3‎‎+‎‎39‎‎4‎ 答案:B 解析:设AB=a,则由AC2=AB2+BC2-2AB·BCcosB知7=a2+4-2a,即a2-2a-3=0,‎ ‎∴a=3(负值舍去).‎ ‎∴BC边上的高为AB·sinB=3×‎3‎‎2‎‎=‎‎3‎‎3‎‎2‎.‎ ‎20.已知圆(x-1)2+y2=‎3‎‎4‎的一条切线y=kx与双曲线C:x‎2‎a‎2‎‎-‎y‎2‎b‎2‎=1(a>0,b>0)有两个交点,则双曲线C的离心率的取值范围是(　　)‎ A.(1,‎3‎) B.(1,2)‎ C.(‎3‎,+∞) D.(2,+∞)‎ 答案:D 解析:由已知得‎|k|‎k‎2‎‎+1‎‎=‎‎3‎‎2‎,解得k2=3.‎ 由y=kx,‎x‎2‎a‎2‎‎-y‎2‎b‎2‎=1,‎消去y,得(b2-a2k2)x2-a2b2=0,‎ 则4(b2-a2k2)a2b2>0,即b2>a2k2.‎ 因为c2=a2+b2,所以c2>(k2+1)a2.‎ 所以e2>k2+1=4,即e>2.故选D.‎ ‎21.已知函数f(x)=cos‎2x-‎π‎2‎‎+‎xx‎2‎‎+1‎+1,则f(x)的最大值与最小值的和为(　　)‎ A.0 B.1 C.2 D.4‎ 答案:C 解析:因为f(x)=cos‎2x-‎π‎2‎‎+‎xx‎2‎‎+1‎+1=sin2x+xx‎2‎‎+1‎+1,‎ 又因为y=sin2x,y=xx‎2‎‎+1‎都是奇函数,‎ 所以设g(x)=f(x)-1=sin2x+xx‎2‎‎+1‎,则g(x)为奇函数,即g(x)的图象关于点(0,0)对称,‎ 所以f(x)=g(x)+1的图象关于点(0,1)对称.‎ 故f(x)的最大值和最小值也关于点(0,1)对称,因此它们的和为2.‎ 故选C.‎ ‎22.设集合A={x|x+2>0},B=xy=‎‎1‎‎3-x,则A∩B=　　　　　. ‎ 答案:{x|-2-2},B={x|x<3},则A∩B={x|-20,b>0)的一个焦点.若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为　　　　　. ‎ 答案:‎‎5‎ 解析:不妨设F(c,0)为双曲线的右焦点,虚轴的一个端点为B(0,b).依题意得点P为(-c,2b).因为点P在双曲线上,所以‎(-c‎)‎‎2‎a‎2‎‎-‎‎(2b‎)‎‎2‎b‎2‎=1,得c‎2‎a‎2‎=5,即e2=5.因为e>1,所以e=‎5‎.‎ ‎26.(x+2)5的展开式中,x2的系数等于　　　　　.(用数字作答). ‎ 答案:80‎ ‎27.若函数f(x)=kx-cos x在区间π‎3‎‎,‎‎5π‎6‎内单调递增,则k的取值范围是　　　　　. ‎ 答案:‎‎-‎1‎‎2‎,+∞‎ 解析:由函数f(x)=kx-cosx,‎ 可得f'(x)=k+sinx.‎ 因为函数f(x)=kx-cosx在区间π‎3‎‎,‎‎5π‎6‎内单调递增,‎ 则k+sinx≥0在区间π‎3‎‎,‎‎5π‎6‎内恒成立.‎ 当x∈π‎3‎‎,‎‎5π‎6‎时,‎ sinx∈‎1‎‎2‎‎,1‎,-sinx∈‎-1,-‎‎1‎‎2‎.‎ 由k≥-sinx,‎ 可得k≥-‎1‎‎2‎.‎