- 2021-05-12 发布 |
- 37.5 KB |
- 36页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习(理)专题五第二讲点、直线、平面之间的位置关系学案(全国通用)
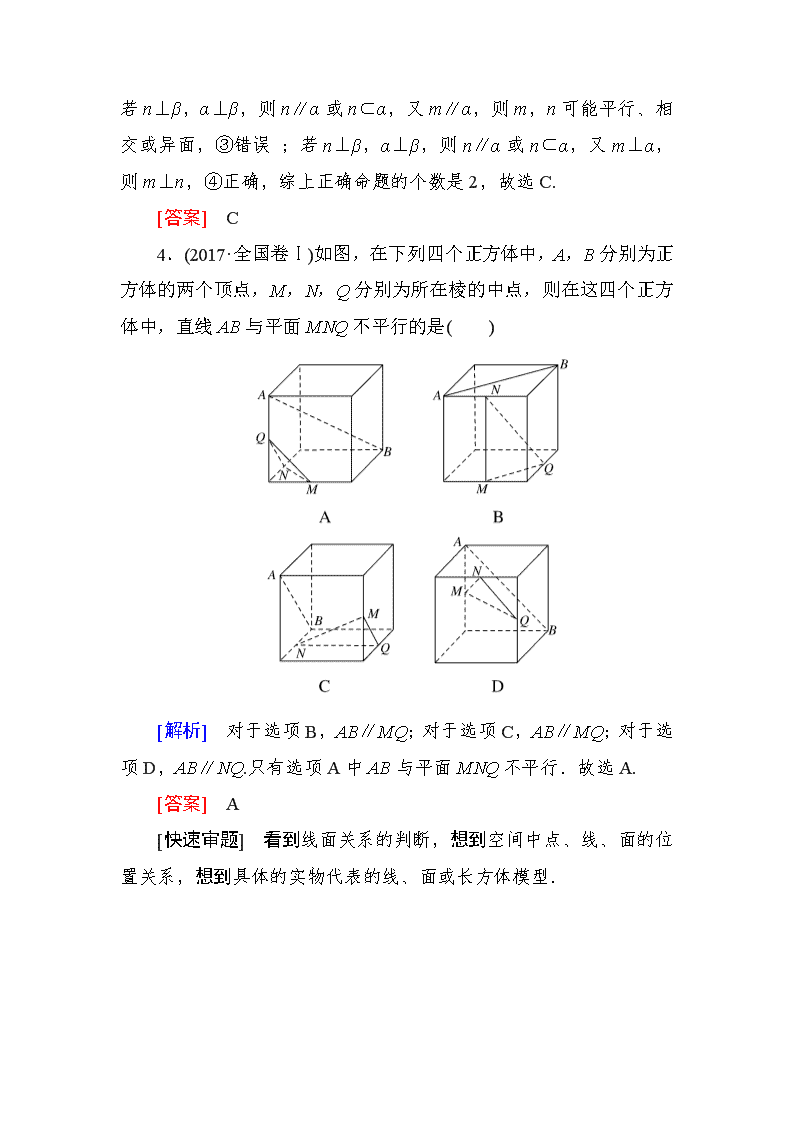
第二讲 点、直线、平面之间的位置关系 考点一 空间线面位置关系的判断 1.直线、平面平行的判定及其性质 (1)线面平行的判定定理:a⊄α,b⊂α,a∥b,⇒a∥α. (2)线面平行的性质定理:a∥α,a⊂β,α∩β=b,⇒a∥b. (3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α,⇒α∥β. (4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b,⇒a∥b. 2.直线、平面垂直的判定及其性质 (1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n,⇒l⊥α. (2)线面垂直的性质定理:a⊥α,b⊥α,⇒a∥b. (3)面面垂直的判定定理:a⊂β,a⊥α,⇒α⊥β. (4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l,⇒a⊥β. [对点训练] 1.(2018·安徽黄山二模)下列说法中,错误的是( ) A.若平面α∥平面β,平面α∩平面γ=l,平面β∩平面γ=m,则l∥m B.若平面α⊥平面β,平面α∩平面β=l,m⊂α,m⊥l,则m⊥β C.若直线l⊥平面α,平面α⊥平面β,则l∥β D.若直线l∥平面α,平面α∩平面β=m,直线l⊂平面β,则 l∥m [解析] 对于A,由面面平行的性质定理可知为真命题,故A正确;对于B,由面面垂直的性质定理可知为真命题,故B正确;对于C,若l⊥α,α⊥β,则l∥β或l⊂β,故C错误;对于D,由线面平行的性质定理可知为真命题,故D正确.综上,选C. [答案] C 2.(2018·湖北重点中学联考)设m,n是平面α内的两条不同直线,l1,l2是平面β内两条相交直线,则α⊥β的一个充分不必要条件是( ) A.l1⊥m,l1⊥n B.m⊥l1,m⊥l2 C.m⊥l1,n⊥l2 D.m∥n,l1⊥n [解析] 由m⊥l1,m⊥l2及已知条件可得m⊥β,又m⊂α,所以α⊥β;反之,α⊥β时未必有m⊥l1,m⊥l2,故“m⊥l1,m⊥l2”是“α⊥β”的充分不必要条件,其余选项均推不出α⊥β,故选B. [答案] B 3.(2018·潍坊模拟)已知两条不同的直线m,n和两个不同的平面α,β,以下四个命题: ①若m∥α,n∥β,且α∥β,则m∥n; ②若m⊥α,n∥β,且α∥β,则m⊥n; ③若m∥α,n⊥β,且α⊥β,则m∥n; ④若m⊥α,n⊥β,且α⊥β,则m⊥n. 其中正确命题的个数是( ) A.4 B.3 C.2 D.1 [解析] 若m∥α,n∥β,且α∥β,则m,n可能平行、相交或异面,①错误;若m⊥α,α∥β,则m⊥β,又n∥β,则m⊥n,② 正确;若n⊥β,α⊥β,则n∥α或n⊂α,又m∥α,则m,n可能平行、相交或异面,③错误 ;若n⊥β,α⊥β,则n∥α或n⊂α,又m⊥α,则m⊥n,④正确,综上正确命题的个数是2,故选C. [答案] C 4.(2017·全国卷Ⅰ)如图,在下列四个正方体中,A,B分别为正方体的两个顶点,M,N,Q分别为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( ) [解析] 对于选项B,AB∥MQ;对于选项C,AB∥MQ;对于选项D,AB∥NQ.只有选项A中AB与平面MNQ不平行.故选A. [答案] A [快速审题] 看到线面关系的判断,想到空间中点、线、面的位置关系,想到具体的实物代表的线、面或长方体模型. 空间线面位置关系判定的三种方法 (1)定理法:借助空间线面位置关系的判定定理和性质定理逐项判断来解决问题. (2)模型法:借助空间几何模型,如在长方体、四面体等模型中观察线面位置关系,结合有关定理作出选择. (3)反证法:当从正面较难入手时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断. 考点二 空间中平行、垂直关系的证明 平行关系及垂直关系的转化 [证明] (1)如图所示,连接AB1交A1B于E,连接ED. ∵ABC-A1B1C1是直三棱柱,且AB=BB1, ∴侧面ABB1A1是正方形, ∴E是AB1的中点,又已知D为AC的中点, ∴在△AB1C中,ED是中位线, ∴B1C∥ED,又B1C⊄平面A1BD,ED⊂平面A1BD, ∴B1C∥平面A1BD. (2)∵AC1⊥平面A1BD. ∴AC1⊥A1B. ∵侧面ABB1A1是正方形,∴A1B⊥AB1. 又AC1∩AB1=A, ∴A1B⊥平面AB1C1,∴A1B⊥B1C1. 又∵ABC-A1B1C1是直三棱柱, ∴BB1⊥B1C1,又BB1∩A1B=B, ∴B1C1⊥平面ABB1A1. [探究追问] 在本例(2)的条件下,设AB=1,求三棱锥B-A1C1D的体积. [解] ∵AB=BC,D为AC的中点, ∴BD⊥AC,∴BD⊥平面DC1A1. ∴BD是三棱锥B-A1C1D的高. 由(2)知B1C1⊥平面ABB1A1, ∵B1C1∥BC,∴BC⊥平面ABB1A1. ∵AB⊂平面ABB1A1, ∴BC⊥AB,∴△ABC是等腰直角三角形, 又∵AB=BC=1,∴BD=, ∴AC=A1C1=. ∴三棱锥B-A1C1D的体积V=·BD·S△A1C1D=××A1C1·AA1=××1=. (1)证明线线平行的4种常用方法 ①利用平行公理,即证两直线同时和第三条直线平行; ②利用平行四边形进行平行转换; ③利用三角形的中位线定理证线线平行; ④利用线面平行、面面平行的性质定理进行平行转换. (2)证明线线垂直的3种常用方法 ①利用等腰三角形底边中线即高线的性质; ②勾股定理; ③线面垂直的性质:即要证两线垂直,只需证明一线垂直于另一线所在的平面. [对点训练] (2018·西宁模拟)如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC=. (1)求证:平面BCD⊥平面CDE; (2)若N为线段DE的中点,求证:平面AMN∥平面BEC. [证明] (1)∵AB=AD=2,AB⊥AD,M为线段BD的中点, ∴AM=BD=,AM⊥BD. ∵AE⊥平面ABD,MC∥AE, ∴MC⊥平面ABD, ∵AM⊂平面ABD. ∴MC⊥AM,又MC∩BD=M, ∴AM⊥平面BCD. 又AE=MC=, ∴四边形AMCE为平行四边形, ∴EC∥AM, ∴EC⊥平面BCD, ∵EC⊂平面CDE, ∴平面BCD⊥平面CDE. (2)∵M为BD的中点,N为DE的中点, ∴MN∥BE.∵MN⊄平面BEC,BE⊂平面BEC. ∴MN∥面BEC. 由(1)知EC∥AM,∵EC⊂平面BEC,AM⊄平面BEC. ∴AM∥面BEC, 又∵AM∩MN=M.AM⊂平面AMN,MN⊂平面AMN. ∴平面AMN∥平面BEC.考点三 空间角的求解 1.求异面直线所成的角 (1)定义法:平移两条异面直线中的一条或两条成相交直线,其所成锐角(或直角)即为所求. (2)向量法:若异面直线a,b的方向向量分别为a,b ,异面直线所成的角为θ,则cosθ=|cos〈a,b〉|=. 2.向量法求线面所成的角 求出平面的法向量n,直线的方向向量a,设线面所成的角 为θ,则sinθ=|cos〈n,a〉|=. 3.向量法求二面角 求出二面角α-l-β的两个半平面α与β的法向量n1,n2,若二面角α-l-β所成的角θ为锐角,则cosθ=|cos〈n1,n2〉|=;若二面角α-l-β所成的角θ为钝角,则cosθ=-|cos〈n1,n2〉|=-. [解] (1)证法一:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2, 所以A1B+AB=AA,故AB1⊥A1B1. 由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=, 由AB=BC=2,∠ABC=120°得AC=2, 由CC1⊥AC,得AC1=,所以AB+B1C=AC,故AB1⊥B1C1.又因为B1C1∩A1B1=B1, 因此AB1⊥平面A1B1C1. 证法二:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz. 由题意知各点坐标如下: A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1). 因此=(1,,2),=(1,,-2),=(0,2,-3). 由·=0得AB1⊥A1B1. 由·=0得AB1⊥A1C1. 又因为A1B1∩A1C1=B1,所以AB1⊥平面A1B1C1. (2)设直线AC1与平面ABB1所成的角为θ. 由(1)可知=(0,2,1),=(1,,0),=(0,0,2). 设平面ABB1的法向量n=(x,y,z). 由即 可取n=(-,1,0). 所以sinθ=|cos〈,n〉|==. 因此,直线AC1与平面ABB1所成的角的正弦值是. [解] (1)证明:由题设可得,△ABD≌△CBD,从而AD=DC. 又△ACD是直角三角形,所以∠ADC=90°. 取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO. 又由于△ABC是正三角形,故BO⊥AC. 所以∠DOB为二面角D-AC-B的平面角. 在Rt△AOB中,BO2+AO2=AB2. 又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°. 所以平面ACD⊥平面ABC. (2)由题设及(1)知,OA,OB,OD两两垂直. 以O为坐标原点,的方向为x轴正方向,|| 为单位长度,建立如图所示的空间直角坐标系O-xyz.则A(1,0,0),B(0,,0),C(-1,0,0),D(0,0,1). 由题设知,四面体ABCE的体积为四面体ABCD的体积为,从而E到平面ABC的距离为D到平面ABC的距离的,即E为DB的中点,得E.故=(-1,0,1),=(-2,0,0),= . 设n=(x,y,z)是平面DAE的法向量, 则即 可取n=. 设m是平面AEC的法向量,则 同理可取m=(0,-1,). 则cos〈n,m〉==. 易知二面角D-AE-C为锐二面角, 所以二面角D-AE-C的余弦值为. 向量法求线面角、二面角需破4“关” (1)“建系关”:构建恰当的空间直角坐标系; (2)“坐标关”:准确求解相关点的坐标; (3)“向量关”:准确求出直线的方向向量和平面的法向量; (4)“公式关”:准确利用公式进行求解及转化. [对点训练] 1.[角度1](2018·河北唐山模拟)已知P是△ABC所在平面外一点,M,N分别是AB,PC的中点,若MN=BC=4,PA=4,则异面直线PA与MN所成角的大小是( ) A.30° B.45° C.60° D.90° [解析] 取AC的中点O,连接OM,ON,则ON∥AP,ON=AP,OM∥BC,OM=BC,所以异面直线PA与MN所成的角为∠ONM(或其补角),在△ONM中,OM=2,ON=2,MN=4,由勾股定理的逆定理得OM⊥ON,则∠ONM=30°.故选A. [答案] A 2.[角度2](2018·郑州模拟)如图,在△ABC中,∠ABC=,O为AB边上一点,且3OB=3OC=2AB,已知PO⊥平面ABC,2DA=2AO= PO,且DA∥PO. (1)求证:平面PBD⊥平面COD; (2)求直线PD与平面BDC所成角的正弦值. [解] (1)证明:∵OB=OC,又∵∠ABC=, ∴∠OCB=,∴∠BOC=. ∴CO⊥AB. 又PO⊥平面ABC,OC⊂平面ABC,∴PO⊥OC. 又∵PO,AB⊂平面PAB,PO∩AB=O, ∴CO⊥平面PAB,即CO⊥平面PDB. 又CO⊂平面COD,∴平面PDB⊥平面COD. (2)以OC,OB,OP所在射线分别为x,y,z 轴,建立空间直角坐标系,如图所示. 设OA=1,则PO=OB=OC=2,DA=1. 则C(2,0,0),B(0,2,0),P(0,0,2),D(0,-1,1), ∴=(0,-1,-1),=(2,-2,0),=(0,-3,1). 设平面BDC的一个法向量为n=(x,y,z), ∴∴ 令y=1,则x=1,z=3,∴n=(1,1,3). 设PD与平面BDC所成的角为θ, 则sinθ= ==. 即直线PD与平面BDC所成角的正弦值为. 3.[角度3]如图,已知在四棱锥P-ABCD中,点O为AB的中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3. (1)求证:平面PAB⊥平面ABCD. (2)求二面角O-PD-C的余弦值. [解] (1)证明:∵AD∥BC,AB ⊥BC,BC=AB=2,AD=3, ∴OC=,OD=,CD=. ∵OD2=OC2+CD2, ∴OC⊥CD. 又平面POC⊥平面ABCD,且平面POC∩平面ABCD=OC,CD⊂平面ABCD,∴CD⊥平面POC. ∵PO⊂平面POC,∴CD⊥PO. 又∵PA=PB=AB,点O为AB的中点. ∴PO⊥AB,由题易知,AB,CD在平面ABCD内,且它们不平行,则必相交于某一点,∴PO⊥底面ABCD. 又∵PO⊂平面PAB, ∴平面PAB⊥平面ABCD. (2)以点O为原点,如图所示建立空间直角坐标系O-xyz, 则P(0,0,),D(-1,3,0),C(1,2,0), ∴=(0,0,),=(-1,3,0),=(-1,-2,),=(-2,1,0). 设平面OPD的一个法向量为m=(x1,y1,z1),平面PCD的一个法向量为n=(x2,y2,z2), 则由可得取y1=1,得 即m=(3,1,0), 同理可得,n=(,2,5), ∴cos〈m,n〉===. 又由图可知二面角O-PD-C的平面角为锐角,故二面角O-PD-C的余弦值为. 1.(2018·浙江卷)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 [解析] ∵m⊄α,n⊂α,m∥n,∴m∥α,故充分性成立.而由m∥α,n⊂α,得m∥n或m与n异面,故必要性不成立.故选A. [答案] A 2.(2017·全国卷Ⅱ)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( ) A. B. C. D. [解析] 解法一:将直三棱柱ABC-A1B1C1补形成直四棱柱ABCD-A1B1C1D1(如图),连接AD1,B1D1,则AD1∥BC1.则∠B1AD1(或其补角)为异面直线AB1与BC1所成的角,易求得AB1=,BC1=AD1= ,B1D1=.由余弦定理得cos∠B1AD1=.故选C. 解法二:以B为坐标原点,,的方向分别为y,z轴的正方向,建立如图所示的空间直角坐标系,则B(0,0,0). ∵∠ABC=120°,BC=1,AB=2,BB1=1, ∴A(0,2,0),B1(0,0,1),C1. ∴=(0,-2,1),=. 设异面直线AB1与BC1所成的角为θ, 则cosθ====,故选C. [答案] C 3.(2017·全国卷Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题: ①如果m⊥n,m⊥α,n∥β,那么α⊥β. ②如果m⊥α,n∥α,那么m⊥n. ③如果α∥β,m⊂α,那么m∥β. ④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等. 其中正确的命题有________.(填写所有正确命题的编号) [解析] 对于①,由m⊥n,m⊥α可得n∥α或n在α内,当n∥β时,α与β可能相交,也可能平行,故①错误;对于②,过直线n作平面与平面α交于直线c,由n∥α可知n∥c,∵m⊥α,∴m⊥c,∴m⊥n,故②正确;对于③,由两个平面平行的性质可知正确;对于④,由线面所成角的定义和等角定理可知其正确,故正确的有②③④. [答案] ②③④ 4.(2018·北京卷)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2. (1)求证:AC⊥平面BEF; (2)求二面角B-CD-C1的余弦值; (3)证明:直线FG与平面BCD相交. [解] (1)证明:在三棱柱ABC-A1B1C1中, 因为CC1⊥平面ABC,所以四边形A1ACC1为矩形. 又E,F分别为AC,A1C1的中点,所以AC⊥EF. 因为AB=BC,E为AC中点,所以AC⊥BE, 又因为BE∩EF=E,所以AC⊥平面BEF. (2)由(1)知AC⊥EF,AC⊥BE,EF∥CC1. 又CC1⊥平面ABC,所以EF⊥平面ABC. 因为BE⊂平面ABC,所以EF⊥BE. 如图建立空间直角坐标系E-xyz. 由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1). 所以=(-1,-2,0),=(1,-2,1). 设平面BCD的法向量为n=(x0,y0,z0), 则即 令y0=-1,则x0=2,z0=-4.于是n=(2,-1,-4). 又因为平面CC1D的一个法向量为=(0,2,0), 所以cos〈n,〉==-. 由题知二面角B-CD-C1为钝角,所以其余弦值为-. (3)证明:由(2)知平面BCD的一个法向量为n=(2,-1,-4),=(0,2,-1). 因为n·=2×0+(-1)×2+(-4)×(-1)=2≠0,所以直线FG与平面BCD相交. 1.高考对此部分的命题较为稳定,一般为“一小一大”或“一大”,即一道选择或填空题和一道解答题或一道解答题. 2.选择题一般在第3~5题的位置,填空题一般在第14题的位置,多考查线面位置关系的判断,难度较小. 3.解答题多出现在第18或19题的位置,考查空间中平行或垂直关系的证明、利用空间向量求异面直线所成的角、线面角或二面角,难度中等. 热点课题13 立体几何中的“翻折”问题 [感悟体验] (2018·安徽合肥二模)如图1,矩形ABCD中,AB=1,AD=2,点E为AD的中点,沿BE将△ABE折起至△PBE,如图2所示,点P在平面BCDE上的射影O点落在BE上. (1)求证:BP⊥CE. (2)求二面角B-PC-D的余弦值. [解] (1)证明:点P在平面BCDE上的射影O点落在BE上,∴PO⊥平面BCDE,∴PO⊥CE. 又BE=CE=,BC=2,则BE2+CE2=BC2,∴BE⊥CE,又BE∩PO=O,BE⊂平面PBE,PO⊂平面PBE,∴CE⊥平面PBE.∵BP⊂平面PBE,∴BP⊥CE. (2)以点O为坐标原点,以过点O且平行于CD的直线为x轴,过点O且垂直于CD的直线为y轴,直线PO为z轴,建立如图所示的空间直角坐标系. 则B,C,D,P, ∴=(-1,0,0),=, =,=(0,2,0). 设平面PCD的一个法向量为n1=(x1,y1,z1), 则 即 令z1=,可得n1=. 设平面PBC的法向量为n2=(x2,y2,z2). 则即 令z2=,可得n2=(2,0,). ∴cos〈n1,n2〉==. 又由图可知,二面角B-PC-D为钝二面角,则二面角B-PC-D的余弦值为-. 专题跟踪训练(二十二) 一、选择题 1.(2018·中原名校联盟联考)已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是( ) A.α⊥β且m⊂α B.α⊥β且m∥α C.m∥n且n⊥β D.m⊥n且n∥β [解析] 对于选项A,α⊥β且m⊂α,可得m∥β或m与β相交或m⊂β,故A不成立;对于选项B,α⊥β且m∥α,可得m⊂β或m∥β或m与β相交,故B不成立;对于选项C,m∥n且n⊥β,则m⊥β,故C正确;对于选项D,由m⊥n且n∥β,可得m∥β或m与β相交或m⊂β,故D不成立.故选C. [答案] C 2.已知直线m,l与平面α,β,γ满足β∩γ=l,l∥α,m⊂α,m⊥γ,则下列命题一定正确的是( ) A.α⊥γ且l⊥m B.α⊥γ且m∥β C.m∥β且l⊥m D.α∥β且α⊥γ [解析] ∵m⊂α,m⊥γ,∴α⊥γ.又∵β∩γ=l,∴l⊂γ,∴l⊥m.故选A. [答案] A 3.(2018·内蒙古赤峰模拟)已知三条不重合的直线m,n,l和两个不重合的平面α,β,下列命题中正确命题的个数为( ) ①若m∥n,n⊂α,则m∥α; ②若l⊥α,m⊥β且l⊥m,则α⊥β; ③若l⊥n,m⊥n,则l∥m; ④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α. A.1 B.2 C.3 D.4 [解析] ①若m∥n,n⊂α,则m∥α或m⊂α,不正确;②若l⊥α,m⊥β,且l⊥m,由面面垂直的判定定理可得α⊥β,正确;③若l⊥n,m⊥n,则l与m平行、相交或为异面直线,不正确;④若α⊥β,α∩β=m,n⊂β,n⊥m,由面面垂直的性质定理得n⊥α ,因此正确.综上可知只有②④正确.故选B. [答案] B 4.[原创题]如图所示,三棱锥P-ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为( ) A.- B. C.- D. [解析] 如图所示,取BC的中点E,连接DE,AE.则在△PBC中,PD=DB,BE=EC,所以DE∥PC,且DE=PC.故∠EDA为异面直线PC,AD所成的角或其补角.因为PA⊥平面ABC,所以PA⊥AC,PA⊥AB.在Rt△ABC中,AC===2;在Rt△PAC中,PC===2.故DE=PC=.在Rt△PAB中,PB===2;又PD=DB,所以AD=PB=.在Rt△EAB中,AE===.在△DAE中,cos∠ADE===-.设异面直线PC,AD所成的角为θ,则cosθ =|cos∠ADE|=.故选D. [答案] D 5.(2018·温州十校联考)如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三种说法中正确的个数是( ) ①存在点E使得直线SA⊥平面SBC; ②平面SBC内存在直线与SA平行; ③平面ABCE内存在直线与平面SAE平行. A.0 B.1 C.2 D.3 [解析] 由题图,得SA⊥SE,若存在点E使得直线SA⊥平面SBC,则SA⊥SB,SA⊥SC,则SC,SB,SE三线共面,则点E与点C重合,与题设矛盾,故①错误;因为SA与平面SBC相交,所以在平面SBC内不存在直线与SA平行,故②错误;显然,在平面ABCE内,存在直线与AE平行,由线面平行的判定定理得平面ABCE 内存在直线与平面SAE平行,故③正确.选B. [答案] B 6.(2018·河北五校联考)在长方体ABCD-A1B1C1D1中,AB=AD=4,AA1=2.过点A1作平面α与AB,AD分别交于M,N两点,若AA1与平面α所成的角为45°,则截面A1MN面积的最小值是( ) A.2 B.4 C.4 D.8 [解析] 如图,过点A作AE⊥MN,连接A1E, ∵A1A⊥平面ABCD,∴A1A⊥MN,又∵A1A∩AE=A,∴MN⊥平面A1AE,∴A1E⊥MN,平面A1AE⊥平面A1MN,∴∠AA1E为AA1与平面A1MN所成的角, ∴∠AA1E=45°,在Rt△A1AE中,∵AA1=2,∴AE=2,A1E=2,在Rt△MAN中,由射影定理得ME·EN=AE2=4,由基本不等式得MN=ME+EN≥2=4,当且仅当ME=EN,即E为MN的中点时等号成立,∴截面A1MN面积的最小值为×4×2=4,故选B. [答案] B 二、填空题 7.(2018·定州二模)如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF= ________. [解析] 根据题意,因为EF∥平面AB1C,EF⊂平面ABCD,平面ABCD∩平面AB1C=AC,所以EF∥AC.又E是AD的中点,所以F是CD的中点.因为在Rt△DEF中,DE=DF=1,故EF=. [答案] 8.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条. [解析] 过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线只可能落在平面DEFG中(其中D、E、F、G分别为AC,BC,B1C1,A1C1的中点).易知经过D、E、F、G中任意两点的直线共有C=6条. [答案] 6 9.(2018·山东烟台二模)如图是一张矩形白纸ABCD,AB=10,AD =10,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是________.(写出所有正确命题的序号) ①当平面ABE∥平面CDF时,AC∥平面BFDE; ②当平面ABE∥平面CDF时,AE∥CD; ③当A、C重合于点P时,PG⊥PD; ④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150π. [解析] 在△ABE中,tan∠ABE=,在△ACD中,tan∠CAD=,所以∠ABE=∠DAC,由题意,将△ABE,△DCF沿BE,DF折起,且A,C在平面BEDF同侧,此时A、C、G、H四点在同一平面内,平面ABE∩平面AGHC=AG,平面CDF∩平面AGHC=CH,当平面ABE∥平面CDF时,得到AG∥CH,显然AG=CH,所以四边形AGHC为平行四边形,所以AC∥GH,进而可得AC∥平面BFDE,故①正确;由于折叠后,直线AE与直线CD为异面直线,所以AE与CD不平行,故②不正确;当A、C重合于点P时,可得PG=,PD=10,又GD=10,∴PG2+PD2≠GD2,所以PG与PD不垂直,故③不正确;当A,C重合于点P时,在三棱锥P-DEF中,△EFD 与△FCD均为直角三角形,所以DF为外接球的直径,即R==,所以外接球的表面积为S=4πR2=4π×2=150π,故④正确.综上,正确命题的序号为①④. [答案] ①④ 三、解答题 10.(2018·河南洛阳一模)如图,在四棱锥E-ABCD中,△EAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=AB,且AE⊥BD. (1)证明:平面EBD⊥平面EAD; (2)若△EAD的面积为,求点C到平面EBD的距离. [解] (1)证明:如图,取AB的中点M,连接DM,则由题意可知四边形BCDM为平行四边形,∴DM=CB=AD=AB, 即点D在以线段AB为直径的圆上, ∴BD⊥AD, 又AE⊥BD,且AE∩AD=A, ∴BD⊥平面EAD. ∵BD⊂平面EBD,∴平面EBD⊥平面EAD. (2)∵BD⊥平面EAD,且BD⊂平面ABCD,∴平面ABCD⊥平面EAD. ∵等边△EAD的面积为,∴AD=AE=ED=2, 取AD的中点O,连接EO,则EO⊥AD,EO=, ∵平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD, ∴EO⊥平面ABCD. 由(1)知△ABD,△EBD都是直角三角形, ∴BD==2, S△EBD=ED·BD=2, 设点C到平面EBD的距离为h, 由VC-EBD=VE-BCD,得S△EBD·h=S△BCD·EO, 又S△BCD=BC·CDsin120°=, ∴h=. ∴点C到平面EBD的距离为. 11.(2018·南昌摸底)在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1. (1)证明:BC⊥AB1; (2)若OC=OA,求直线C1D与平面ABC所成角的正弦值. [解] (1)证明:由题意,tan∠ABD==, tan∠AB1B==, 由图可知0<∠ABD,∠AB1B<, 所以∠ABD=∠AB1B, 所以∠ABD+∠BAB1=∠AB1B+∠BAB1=, 所以AB1⊥BD, 又CO⊥侧面ABB1A1,∴AB1⊥CO. 又BD与CO交于点O,所以AB1⊥平面CBD, 又因为BC⊂平面CBD,所以BC⊥AB1. (2)如图,以O为原点,分别以OD,OB1,OC所在的直线为x,y,z轴,建立如图所示的空间直角坐标系O-xyz, 则A, B, C, B1,D, 又因为=2,所以C1. 所以=,=, =. 设平面ABC的法向量为n=(x,y,z), 则根据可得 令x=1,则y=,z=-, 所以n=(1,,-)是平面ABC的一个法向量,设直线C1D与平面ABC所成角为α, 则sinα==. 12.(2018·贵阳监测)如图所示,该几何体由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2. (1)证明:平面PAD⊥平面ABFE; (2)若正四棱锥P-ABCD的高为1,求二面角C-AF-P的余弦值. [解] (1)证明:∵直三棱柱ADE-BCF中,AB⊥平面ADE, ∴AB⊥AD,又AD⊥AF,AB∩AF=A, ∴AD⊥平面ABFE,∵AD⊂平面PAD, ∴平面PAD⊥平面ABFE. (2)∵AD∥BC,AD⊥平面ABFE,∴BC⊥平面ABFE,且AB⊥BF,建立以B为坐标原点,BA,BF,BC所在直线分别为x轴,y轴, z轴的空间直角坐标系,如图所示. ∵正四棱锥P-ABCD的高为1,AE=AD=2, ∴A(2,0,0),E(2,2,0),F(0,2,0),C(0,0,2),P(1,-1,1), ∴=(-2,2,0),=(0,2,-2),=(1,1,-1), 设n1=(x1,1,z1)是平面ACF的一个法向量,则n1⊥,n1⊥, ∴即 解得x1=1,z1=1,即n1=(1,1,1). 设n2=(x2,1,z2)是平面PAF的一个法向量,则 n2⊥,n2⊥, ∴即 解得x2=1,z2=2,即n2=(1,1,2). ∴cos〈n1,n2〉===, 又二面角C-AF-P是锐角, ∴二面角C-AF-P的余弦值是.查看更多