2019年高考数学高分突破复习课件考前冲刺三 第六类

2019年高考数学高分突破复习课件考前冲刺三 第六类

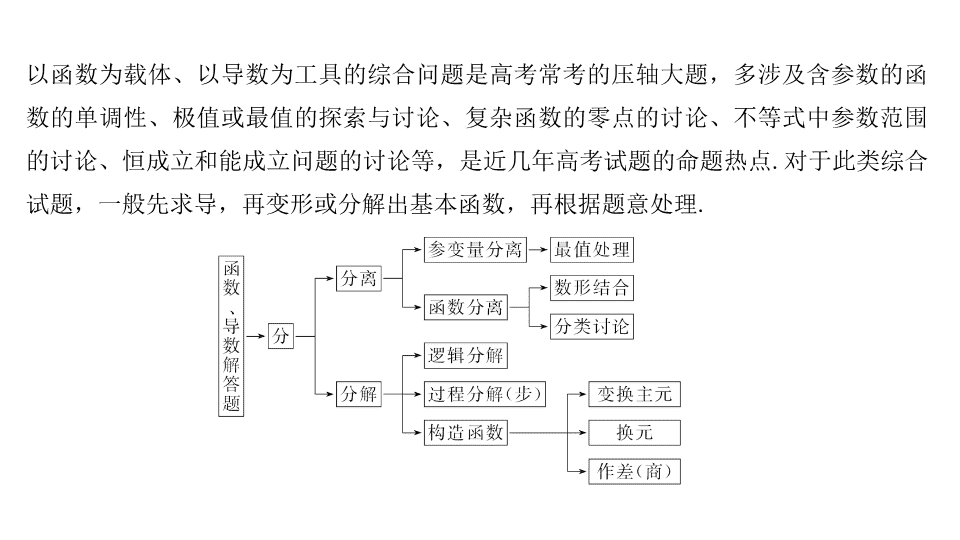
第六类　函数与导数问题重在 “ 分 ” —— 分离、分解 以函数为载体、以导数为工具的综合问题是高考常考的压轴大题，多涉及含参数的函数的单调性、极值或最值的探索与讨论、复杂函数的零点的讨论、不等式中参数范围的讨论、恒成立和能成立问题的讨论等，是近几年高考试题的命题热点 . 对于此类综合试题，一般先求导，再变形或分解出基本函数，再根据题意处理 . 【例 6 】 (2017· 全国 Ⅱ 卷 ) 已知函数 f ( x ) ＝ ax 2 － ax － x ln x ，且 f ( x ) ≥ 0. (1) 求 a ； (2) 证明： f ( x ) 存在唯一的极大值点 x 0 ，且 e － 2 < f ( x 0 )<2 － 2 . (1) 解 　 f ( x ) 的定义域为 (0 ，＋ ∞ ) ， 设 g ( x ) ＝ ax － a － ln x ，则 f ( x ) ＝ xg ( x ) ， ( 分离 ) f ( x ) ≥ 0 等价于 g ( x ) ≥ 0 ， 因为 g (1) ＝ 0 ， g ( x ) ≥ 0 ，故 g ′(1) ＝ 0 ， 当 0< x <1 时， g ′( x )<0 ， g ( x ) 单调递减； 当 x >1 时， g ′( x )>0 ， g ( x ) 单调递增， 所以 x ＝ 1 是 g ( x ) 的极小值点，故 g ( x ) ≥ g (1) ＝ 0. 综上， a ＝ 1. (2) 证明 　由 (1) 知 f ( x ) ＝ x 2 － x － x ln x ， f ′( x ) ＝ 2 x － 2 － ln x ， 设 h ( x ) ＝ 2 x － 2 － ln x ， ( 分解 ) 因为 f ′( x ) ＝ h ( x ) ，所以 x ＝ x 0 是 f ( x ) 的唯一极大值点 . 由 f ′( x 0 ) ＝ 0 得 ln x 0 ＝ 2( x 0 － 1) ，故 f ( x 0 ) ＝ x 0 (1 － x 0 ) . 因为 x ＝ x 0 是 f ( x ) 在 (0 ， 1) 的最大值点， 由 e － 1 ∈ (0 ， 1) ， f ′(e － 1 ) ≠ 0 得 f ( x 0 )> f (e － 1 ) ＝ e － 2 . 所以 e － 2 < f ( x 0 )<2 － 2 . 探究提高 　 1.(1) 分离：把函数 f ( x ) 分离为 x 与 g ( x ) 的积 . (2) 分解：构造 h ( x ) ＝ 2 x － 2 － ln x . 2 . 破解策略：函数与导数压轴题计算复杂、综合性强、难度大 . 可以把参变量分离，把复杂函数分离为基本函数；可把题目分解成几个小题；也可把解题步骤分解为几个小步；注重分步解答，这样，即使解答不完整，也要做到尽可能多拿步骤分 . 【训练 6 】 (2018· 石家庄调研 ) 已知函数 f ( x ) ＝ (2 x ＋ b )e x ， F ( x ) ＝ bx － ln x ， b ∈ R . ( 1) 若 b <0 ，且存在区间 M ，使 f ( x ) 和 F ( x ) 在区间 M 上具有相同的单调性，求实数 b 的取值范围； ( 2) 若 F ( x ＋ 1)> b 对任意 x ∈ (0 ，＋ ∞ ) 恒成立，求实数 b 的取值范围 . 解 　 (1) f ′( x ) ＝ e x (2 x ＋ b ＋ 2) ， ∵ b <0 ， ∴ F ′( x )<0 ，即 F ( x ) 在 (0 ，＋ ∞ ) 上单调递减 . ∵ f ( x ) 和 F ( x ) 在区间 M 上具有相同的单调性， (2) 由 F ( x ＋ 1)> b 得 ln( x ＋ 1) － bx <0. ∴ g ( x ) 在 (0 ，＋ ∞ ) 上递减， ∴ g ( x )< g (0) ＝ 0. 因此实数 b 的取值范围是 [1 ，＋ ∞ ) .