- 2021-05-12 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
近年高考理科立体几何大题汇编
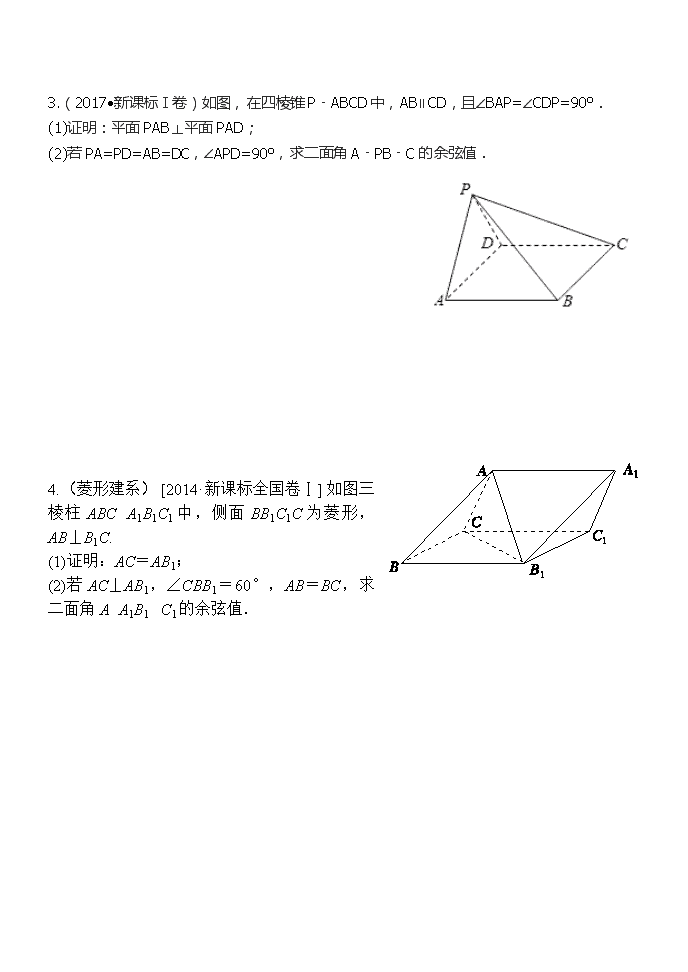
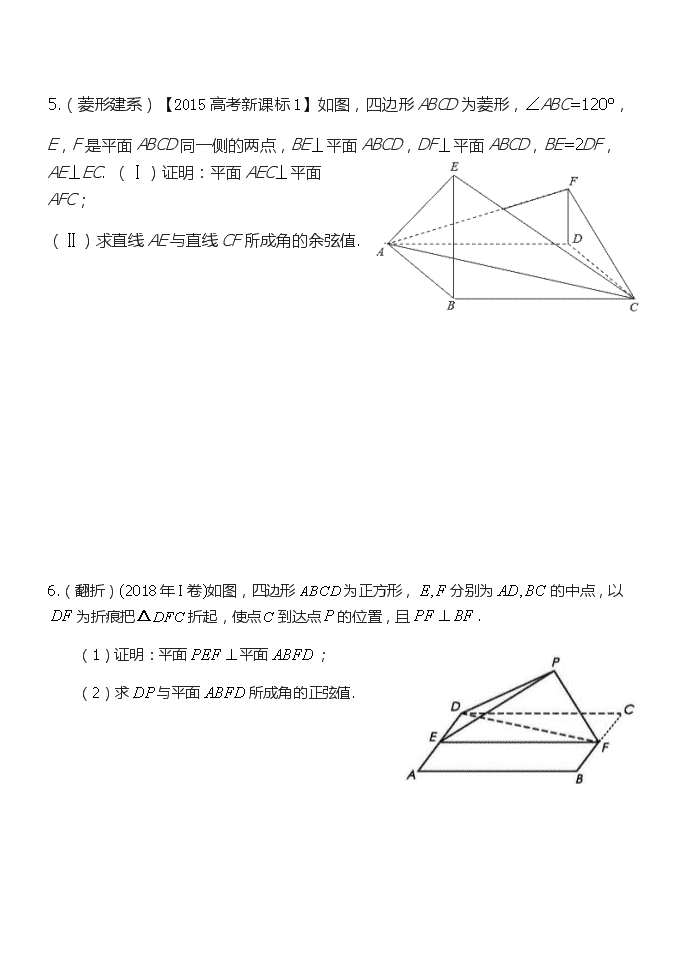
近几年高考理科立体几何大题汇编 1.(2018年III卷)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点. (1)证明:平面平面; (2)当三棱锥体积最大时,求面与面所成二面角的正弦值. 2、[2014·新课标全国卷Ⅱ] 四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. (1)证明:PB∥平面AEC; (2)设二面角DAEC为60°,AP=1,AD=,求三棱锥EACD的体积. 3.(2017•新课标Ⅰ卷)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°. (1)证明:平面PAB⊥平面PAD; (2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值. 4.(菱形建系) [2014·新课标全国卷Ⅰ] 如图三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C. (1)证明:AC=AB1; (2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值. 5.(菱形建系)【2015高考新课标1】如图,四边形ABCD为菱形,∠ABC=120°, E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC. (Ⅰ)证明:平面AEC⊥平面AFC; (Ⅱ)求直线AE与直线CF所成角的余弦值. 6.(翻折)(2018年I卷)如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且. (1)证明:平面平面; (2)求与平面所成角的正弦值. 7.(翻折)(2016年全国II高考)如图,菱形的对角线与交于点,,点分别在上,,交于点.将沿折到位置,. (Ⅰ)证明:平面; (Ⅱ)求二面角的正弦值. 8.(动点问题)(2018年II卷)如图,在三棱锥中,,,为的中点. (1)证明:平面; (2)若点在棱上,且二面角为,求与平面所成角的正弦值. 近几年高考理科立体几何大题汇编 1.(2018年III卷)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点. (1)证明:平面平面; (2)当三棱锥体积最大时,求面与面所成二面角的正弦值. 1.解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM. 因为M为上异于C,D的点,且DC为直径,所以 DM⊥CM. 又 BCCM=C,所以DM⊥平面BMC. 而DM平面AMD,故平面AMD⊥平面BMC. (2)以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz. 当三棱锥M−ABC体积最大时,M为的中点. 由题设得, 设是平面MAB的法向量,则 即 可取. 是平面MCD的法向量,因此 , , 所以面MAB与面MCD所成二面角的正弦值是. 2、[2014·新课标全国卷Ⅱ] 如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. (1)证明:PB∥平面AEC; (2)设二面角DAEC为60°,AP=1,AD=,求三棱锥EACD的体积. 图13 2,解:(1)证明:连接BD交AC于点O,连接EO. 因为ABCD为矩形,所以O为BD的中点. 又E为PD的中点,所以EO∥PB. 因为EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC. (2)因为PA⊥平面ABCD,ABCD为矩形, 所以AB,AD,AP两两垂直. 如图,以A为坐标原点,,AD,AP的方向为x轴、y轴、z轴的正方向,||为单位长,建立空间直角坐标系Axyz,则D,E,=. 设B(m,0,0)(m>0),则C(m,,0),=(m,,0). 设n1=(x,y,z)为平面ACE的法向量, 则即 可取n1=. 又n2=(1,0,0)为平面DAE的法向量, 由题设易知|cos〈n1,n2〉|=,即 =,解得m=. 因为E为PD的中点,所以三棱锥EACD的高为.三棱锥EACD的体积V=××××=. 3.(2017•新课标Ⅰ卷)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°. (1)证明:平面PAB⊥平面PAD; (2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值. 3.【答案】(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD, ∵AB∥CD,∴AB⊥PD, 又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD, ∴AB⊥平面PAD,又AB⊂平面PAB, ∴平面PAB⊥平面PAD; (2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形, 由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形, 在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形, 设PA=AB=2a,则AD= . 取AD中点O,BC中点E,连接PO、OE, 以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系, 则:D( ),B( ),P(0,0, ),C( ). , , . 设平面PBC的一个法向量为 , 由 ,得 ,取y=1,得 . ∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥AD, 又PD⊥PA,PA∩AB=A, ∴PD⊥平面PAB,则 为平面PAB的一个法向量, . ∴cos< >= = . 由图可知,二面角A﹣PB﹣C为钝角, ∴二面角A﹣PB﹣C的余弦值为 . 4.(菱形建系) [2014·新课标全国卷Ⅰ] 如图三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C. (1)证明:AC=AB1; (2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值. 4解:(1)证明:连接BC1,交B1C于点O,连接AO,因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点. 又AB⊥B1C,所以B1C⊥平面ABO. 由于AO⊂平面ABO,故B1C⊥AO. 又B1O=CO,故AC=AB1. (2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO. 又因为AB=BC,所以△BOA≌ △BOC.故OA⊥OB,从而OA,OB,OB1两两垂直. 以O为坐标原点,OB的方向为x轴正方向,|OB|为单位长,建立如图所示的空间直角坐标系O xyz. 因为∠CBB1=60°,所以△CBB1为等边三角形,又AB=BC,则A,B(1,0,0),B1,C. =,=AB=, 1=BC=. 设n=(x,y,z)是平面AA1B1的法向量,则 即所以可取n=(1,,). 设m是平面A1B1C1的法向量, 则同理可取m=(1,-,). 则cos〈n,m〉==. 所以结合图形知二面角A A1B1 C1的余弦值为. 5.(菱形建系)【2015高考新课标1】如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC. (Ⅰ)证明:平面AEC⊥平面AFC; (Ⅱ)求直线AE与直线CF所成角的余弦值. 5.,【答案】(Ⅰ)见解析(Ⅱ) 又∵AE⊥EC,∴EG=,EG⊥AC, 在Rt△EBG中,可得BE=,故DF=. 在Rt△FDG中,可得FG=. 在直角梯形BDFE中,由BD=2,BE=,DF=可得EF=, ∴,∴EG⊥FG, ∵AC∩FG=G,∴EG⊥平面AFC, ∵EG面AEC,∴平面AFC⊥平面AEC. ……6分 (Ⅱ)如图,以G为坐标原点,分别以的方向为轴,y轴正方向,为单位长度,建立空间直角坐标系G-xyz,由(Ⅰ)可得A(0,-,0),E(1,0, ),F(-1,0,),C(0,,0),∴=(1,,),=(-1,-,).…10分 故. 所以直线AE与CF所成的角的余弦值为. ……12分 6.(翻折)(2018年I卷)如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且. (1)证明:平面平面; (2)求与平面所成角的正弦值. 6.解:(1)由已知可得,BF⊥PF,BF⊥EF,所以BF⊥平面PEF. 又平面ABFD,所以平面PEF⊥平面ABFD. (2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD. 以H为坐标原点,的方向为y轴正方向,为单位长,建立如图所示的空间直角坐标系H−xyz. 由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=.又PF=1,EF=2,故PE⊥PF. 可得. 则为平面ABFD的法向量. 设DP与平面ABFD所成角为,则. 所以DP与平面ABFD所成角的正弦值为. 7.(翻折)(2016年全国II高考)如图,菱形的对角线与交于点,,点分别在上,,交于点.将沿折到位置,. (Ⅰ)证明:平面; (Ⅱ)求二面角的正弦值. 7.【解析】⑴证明:∵,∴, ∴.∵四边形为菱形,∴, ∴,∴,∴. ∵,∴;又,,∴, ∴,∴,∴,∴.又∵,∴面. ⑵建立如图坐标系. ,,,, ,,, 设面法向量, 由得,取,∴. 同理可得面的法向量, ∴,∴. 8.(动点问题)(2018年II卷)如图,在三棱锥中,,,为的中点. (1)证明:平面; (2)若点在棱上,且二面角为,求与平面所成角的正弦值. 解:(1)因为,为的中点,所以,且. 连结.因为,所以为等腰直角三角形, 且,. 由知. 由知平面. (2)如图,以为坐标原点,的方向为轴正方向,建立空间直角坐标系. 由已知得取平面的法向量. 设,则. 设平面的法向量为. 由得,可取, 所以.由已知得. 所以.解得(舍去),. 所以.又,所以. 所以与平面所成角的正弦值为.查看更多