2018-2019学年山西省晋中市高一上学期期末调研测试数学试题（解析版）

2018-2019学年山西省晋中市高一上学期期末调研测试数学试题（解析版）

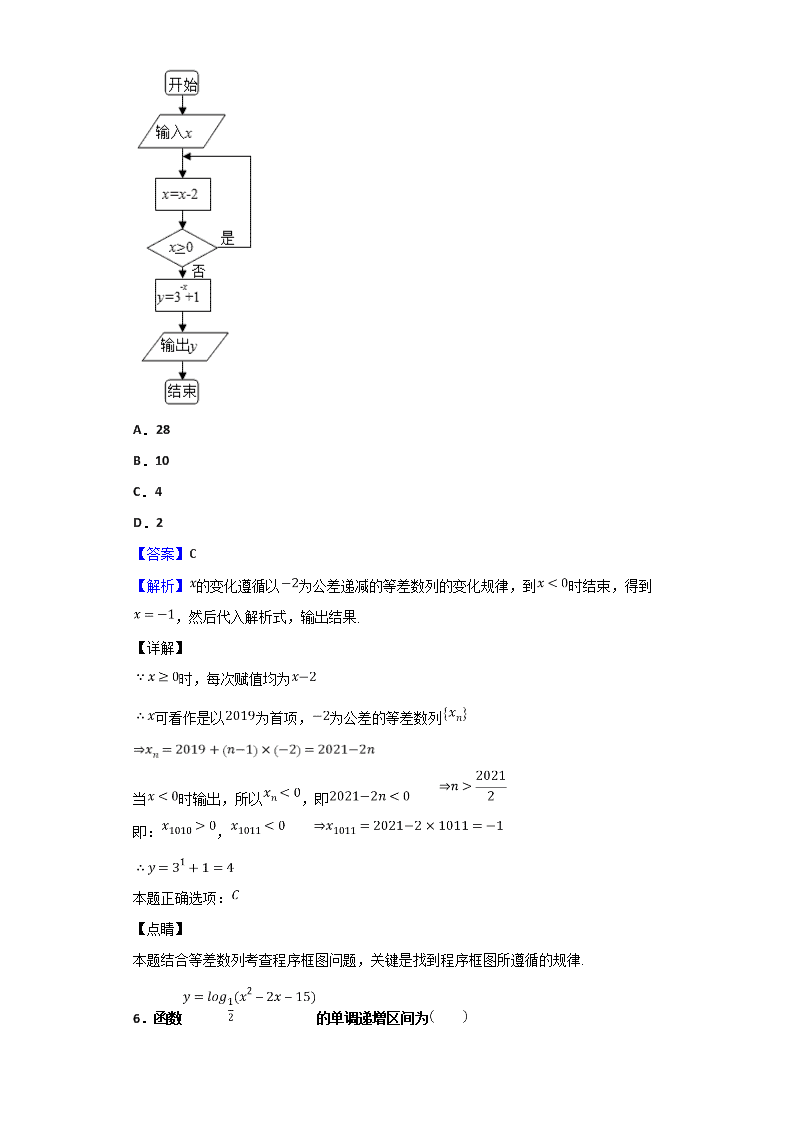
‎2018-2019学年山西省晋中市高一上学期期末调研测试数学试题 一、单选题 ‎1．已知集合，集合，则（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】由题意，求得集合，集合，根据集合的交集的运算，即可求解，得到答案.‎ ‎【详解】‎ 由题意，集合，集合，‎ 根据集合的交集的运算，可得，故选B.‎ ‎【点睛】‎ 本题主要考查了集合的交集的运算问题，其中解答中首先求解集合，再利用集合的交集的运算求解是解答的关键，着重考查了推理与运算能力，属于基础题.‎ ‎2．有一个容量为66的样本，数据的分组及各组的频数如下：‎ ‎，，‎ ‎，，‎ 根据样本的频数分布估计，大于或等于的数据约占　　‎ A． B． C． D．‎ ‎【答案】C ‎【解析】找到大于或等于的频数，除以总数即可.‎ ‎【详解】‎ 由题意知，大于或等于的数据共有：‎ 则约占：‎ 本题正确选项：‎ ‎【点睛】‎ 考查统计中频数与总数的关系，属于基础题.‎ ‎3．秦九韶算法是中国古代求多项式的值的优秀算法，若，当时，用秦九韶算法求　　‎ A．1 B．3 C．4 D．5‎ ‎【答案】C ‎【解析】通过将多项式化成秦九韶算法的形式，代入可得.‎ ‎【详解】‎ 由题意得：‎ 则：‎ 本题正确选项：‎ ‎【点睛】‎ 本题考查秦九韶算法的基本形式，属于基础题.‎ ‎4．下列四组函数中，不表示同一函数的是　　‎ A．与 B．与 C．与 D．与 ‎【答案】D ‎【解析】根据相同函数对定义域和解析式的要求，依次判断各个选项.‎ ‎【详解】‎ 相同函数要求：函数定义域相同，解析式相同 三个选项均满足要求，因此是同一函数 选项：定义域为；定义域为，因此不是同一函数 本题正确选项：‎ ‎【点睛】‎ 本题考查相同函数的概念，关键在于明确相同函数要求定义域和解析式相同，从而可以判断结果.‎ ‎5．执行如图所示程序框图，当输入的x为2019时，输出的　　‎ A．28‎ B．10‎ C．4‎ D．2‎ ‎【答案】C ‎【解析】的变化遵循以为公差递减的等差数列的变化规律，到时结束，得到，然后代入解析式，输出结果.‎ ‎【详解】‎ 时，每次赋值均为 可看作是以为首项，为公差的等差数列 当时输出，所以，即 ‎ 即：， ‎ 本题正确选项：‎ ‎【点睛】‎ 本题结合等差数列考查程序框图问题，关键是找到程序框图所遵循的规律.‎ ‎6．函数的单调递增区间为　　‎ A． B． C． D．‎ ‎【答案】C ‎【解析】结合对数真数大于零，求出定义域；再求出在定义域内的单调递减区间，得到最终结果.‎ ‎【详解】‎ ‎ 或 在定义域内单调递减 根据复合函数单调性可知，只需单调递减即可 ‎ 结合定义域可得单调递增区间为：‎ 本题正确选项：‎ ‎【点睛】‎ 本题考查求解复合函数的单调区间，复合函数单调性遵循“同增异减”原则，易错点在于忽略了函数自身的定义域要求.‎ ‎7．在一不透明袋子中装着标号为1，2，3，4，5，6的六个质地、大小、颜色无差别小球，现从袋子中有放回地随机摸出两个小球，并记录标号，则两标号之和为9的概率是　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】确定所有可能的基本事件总数，再列出标号和为的所有基本事件，根据古典概型可求得概率.‎ ‎【详解】‎ 有放回的摸出两个小球共有：种情况 用表示两次取出的数字编号 标号之和为有：，，，四种情况 所以，概率 本题正确选项：‎ ‎【点睛】‎ 本题考查古典概型的相关知识，对于基本事件个数较少的情况，往往采用列举法来求解，属于基础题.‎ ‎8．远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图所示的是一位母亲记录的孩子自出生后的天数，在从右向左依次排列的不同绳子上打结，满七进一，根据图示可知，孩子已经出生的天数是　　‎ A．336 B．510 C．1326 D．3603‎ ‎【答案】B ‎【解析】试题分析：由题意满七进一，可得该图示为七进制数, 化为十进制数为,故选B.‎ ‎【考点】1、阅读能力及建模能力；2、进位制的应用.‎ ‎9．设，，，则a，b，c的大小关系为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】将化成对数的形式，然后根据真数相同，底数不同的对数的大小关系，得到结果.‎ ‎【详解】‎ 由题意得：‎ 又 ‎ 本题正确选项：‎ ‎【点睛】‎ 本题考查对数大小比较问题，关键在于将对数化为同底或者同真数的对数，然后利用对数函数图像来比较.‎ ‎10．设函数和分别是上的偶函数和奇函数，则下列结论恒成立的是 （ ）‎ A. 是奇函数 ‎ B. 是奇函数 C．是偶函数 ‎ D. 是偶函数 ‎【答案】D ‎【解析】试题分析：根据题意，A.错误，令定义域为，由：，所以是非奇非偶函数；B错误，令定义域为，由：即：，所以是偶函数；C.错误.令定义域为，由：，所以为非奇非偶函数；D.正确. 令定义域为，由，即，所以为偶函数，正确.‎ 综上，答案为D.‎ ‎【考点】1.函数的奇偶性；2.奇偶函数的定义域.‎ ‎11．已知函数是定义在R上的偶函数，且在上是增函数，若对任意，都有恒成立，则实数a的取值范围是　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】根据偶函数的性质，可知函数在上是减函数，根据不等式在上恒成立，可得：在上恒成立，可得的范围.‎ ‎【详解】‎ 为偶函数且在上是增函数 在上是减函数 对任意都有恒成立等价于 ‎ ‎ 当时，取得两个最值 ‎ ‎ 本题正确选项：‎ ‎【点睛】‎ 本题考查函数奇偶性和单调性解抽象函数不等式的问题，关键在于能够通过单调性确定自变量之间的关系，得到关于自变量的不等式.‎ ‎12．设，表示不超过实数的最大整数，则函数的值域是　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】根据不同的范围，求解出的值域，从而得到的值域，同理可得的值域，再根据取整运算得到可能的取值.‎ ‎【详解】‎ 由题意得：，‎ ‎①当时，则，此时，‎ ‎， ，‎ 则 ‎②当时，，‎ ‎， ，‎ ‎③当时，则，此时，‎ ‎， ，‎ 则 综上所述：的值域为 本题正确选项：‎ ‎【点睛】‎ 本题考查新定义运算的问题，解题关键在于能够明确新定义运算的本质，易错点在于忽略与的彼此取值影响，单纯的考虑与整体的值域，造成求解错误.‎ 二、填空题 ‎13．函数的定义域是_______________‎ ‎【答案】‎ ‎【解析】由题要使函数有意义须满足 ‎ ‎14．小明通过做游戏的方式来确定接下来两小时的活动，他随机地往边长为1的正方形内扔一颗豆子，若豆子到各边的距离都大于，则去看电影；若豆子到正方形中心的距离大于，则去打篮球；否则，就在家写作业则小明接下来两小时不在家写作业的概率为______豆子大小可忽略不计 ‎【答案】‎ ‎【解析】根据题意画出图形，求出写作业所对应的区域面积，利用得到结果.‎ ‎【详解】‎ 由题意可知，当豆子落在下图中的空白部分时，小明在家写作业 大正方形面积；阴影正方形面积 空白区域面积：‎ 根据几何概型可知，小明不在家写作业的概率为：‎ 本题正确结果：‎ ‎【点睛】‎ 本题考查几何概型中的面积型，属于基础题.‎ ‎15．若函数为偶函数，则______．‎ ‎【答案】1‎ ‎【解析】为定义域上的偶函数，所以利用特殊值求出的值.‎ ‎【详解】‎ 是定义在上的偶函数 ‎ 即 ‎ ‎ 解得：‎ 本题正确结果：‎ ‎【点睛】‎ 本题考查利用函数奇偶性求解参数值，对于定义域明确的函数，常常采用赋值法来进行求解，相较于定义法，计算量要更小.‎ ‎16．已知函数，若存在实数a，b，c，满足，其中，则abc的取值范围是______．‎ ‎【答案】‎ ‎【解析】根据解析式，画出的图像，可知函数与每段的交点位置，由此可得，再求出的范围后，可确定整体的取值范围.‎ ‎【详解】‎ 由解析式可知图像如下图所示：‎ 由图像可知：‎ 又且时，‎ 可知 ‎ 即 又 ‎ 本题正确结果：‎ ‎【点睛】‎ 本题考查函数图像及方程根的问题，关键在于能够通过函数图像得到的关系.‎ 三、解答题 ‎17．设集合，不等式的解集为B．‎ 当时，求集合A，B；‎ 当时，求实数a的取值范围．‎ ‎【答案】（1）A={x|-1

查看更多