- 2021-05-12 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年黑龙江省大庆市中考数学试卷【含答案;word版本试题;可编辑】
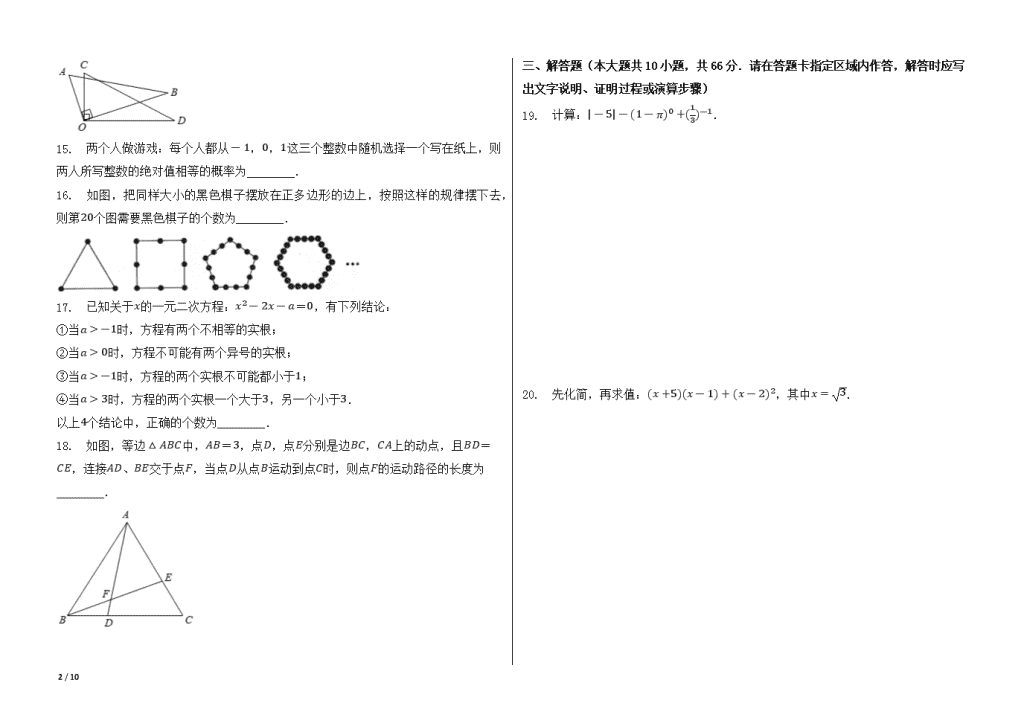
2020年黑龙江省大庆市中考数学试卷 一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上) 1. 在-1,0,π,3这四个数中,最大的数是( ) A.-1 B.0 C.π D.3 2. 天王星围绕太阳公转的轨道半径长约为2900000000km,数字2900000000用科学记数法表示为( ) A.2.9×108 B.2.9×109 C.29×108 D.0.29×1010 3. 若|x+2|+(y-3)2=0,则x-y的值为( ) A.-5 B.5 C.1 D.-1 4. 函数y=2x的自变量x的取值范围是( ) A.x≤0 B.x≠0 C.x≥0 D.x≥12 5. 已知正比例函数y=k1x和反比例函数y=k2x,在同一直角坐标系下的图象如图所示,其中符合k1⋅k2>0的是( ) A.①② B.①④ C.②③ D.③④ 6. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( ) A.1 B.2 C.3 D.4 7. 在一次青年歌手比赛中,七位评委为某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0(单位:分).若去掉一个最高分和一个最低分.则去掉前与去掉后没有改变的一个统计量是( ) A.平均分 B.方差 C.中位数 D.极差 8. 底面半径相等的圆锥与圆柱的高的比为1:3,则圆锥与圆柱的体积的比为( ) A.1:1 B.1:3 C.1:6 D.1:9 9. 已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为( ) A.10+7或5+27 B.15 C.10+7 D.15+37 10. 如图,在边长为2的正方形EFGH中,M,N分别为EF与GH的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当y=52时,x的值为( ) A.74或2+22 B.102或2-22 C.2±22 D.74或102 二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上) 11. 点P(2, 3)关于y轴的对称点Q的坐标为________. 12. 分解因式:a3-4a=________. 13. 一个周长为16cm的三角形,由它的三条中位线构成的三角形的周长为 8 cm. 14. 将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108∘,则∠COB= 10 / 10 ________. 15. 两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为________. 16. 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为________. 17. 已知关于x的一元二次方程:x2-2x-a=0,有下列结论: ①当a>-1时,方程有两个不相等的实根; ②当a>0时,方程不可能有两个异号的实根; ③当a>-1时,方程的两个实根不可能都小于1; ④当a>3时,方程的两个实根一个大于3,另一个小于3. 以上4个结论中,正确的个数为________. 18. 如图,等边△ABC中,AB=3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为________. 三、解答题(本大题共10小题,共66分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) 19. 计算:|-5|-(1-π)0+(13)-1. 20. 先化简,再求值:(x+5)(x-1)+(x-2)2,其中x=3. 10 / 10 21. 解方程:2xx-1-1=4x-1. 22. 如图,AB,CD为两个建筑物,两建筑物底部之间的水平地面上有一点M,从建筑物AB的顶点A测得M点的俯角为45∘,从建筑物CD的顶点C测得M点的俯角为75∘,测得建筑物AB的顶点A的俯角为30∘.若已知建筑物AB的高度为20米,求两建筑物顶点A、C之间的距离(结果精确到1m,参考数据:2≈1.414,3≈1.732). 23. 为了了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如图的频数直方图,图中的a,b满足关系式2a=3b.后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题. (1)求问题中的总体和样本容量; 10 / 10 (2)求a,b的值(请写出必要的计算过程); (3)如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数大约是多少人?(注:该年级共1000名学生) 24. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN. (1)求证:四边形ANCM为平行四边形; (2)若AD=4,AB=2,且MN⊥AC,求DM的长. 25. 期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元. (1)求购买一个甲种、一个乙种笔记本各需多少元? (2)两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两 10 / 10 种笔记本的总费用不超过上一次总费用的90%,求至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值. 26. 如图,反比例函数y=kx与一次函数y=-x-(k+1)的图象在第二象限的交点为A,在第四象限的交点为C,直线AO(O为坐标原点)与函数y=kx的图象交于另一点B.过点A作y轴的平行线,过点B作x轴的平行线,两直线相交于点E,△AEB的面积为6. (1)求反比例函数y=kx的表达式; (2)求点A,C的坐标和△AOC的面积. 27. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC 10 / 10 ,垂足为M,AB、MD的延长线交于点N. (1)求证:MN是⊙O的切线; (2)求证:DN2=BN⋅(BN+AC); (3)若BC=6,cosC=35,求DN的长. 28. 如图,抛物线y=ax2+bx+12与x轴交于A,B两点(B在A的右侧),且经过点C(-1, 7)和点D(5, 7). (1)求抛物线的函数表达式; (2)连接AD,经过点B的直线l与线段AD交于点E,与抛物线交于另一点F.连接CA,CE,CD,△CED的面积与△CAD的面积之比为1:7,点P为直线l上方抛物线上的一个动点,设点P的横坐标为t.当t为何值时,△PFB的面积最大?并求出最大值; (3)在抛物线y=ax2+bx+12上,当m≤x≤n时,y的取值范围是12≤y≤16,求m-n的取值范围.(直接写出结果即可) 10 / 10 参考答案与试题解析 2020年黑龙江省大庆市中考数学试卷 一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上) 1.C 2.B 3.A 4.C 5.B 6.B 7.C 8.D 9.A 10.A 二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上) 11.(-2, 3) 12.a(a+2)(a-2) 13.8 14.72∘ 15.59 16.440 17.①③④ 18.23π3. 三、解答题(本大题共10小题,共66分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) 19.|-5|-(1-π)0+(13)-1 =5-1+3 =7. 20.原式=x2+4x-5+x2-4x+4 =2x2-1, 当x=3时,原式=2(3)2-1=5. 21.方程的两边同乘x-1,得:2x-x+1=4, 解这个方程,得:x=3, 经检验,x=3是原方程的解, ∴ 原方程的解是x=3. 22.两建筑物顶点A、C之间的距离约为35米. 23.1000名学生一分钟的跳绳次数是总体, 40名学生的一分钟跳绳次数是样本容量; 由题意所给数据可知: 10 / 10 50.5∼75.5的有4人, 75.5∼100.5的有16人, ∴ a+b=40-4-16=20, ∵ 2a=3b, ∴ 解得a=12,b=8, 1000×840=200(人), 答:估计该校该年级学生跳绳成绩优秀的人数大约是200人. 24.证明:∵ 在矩形ABCD中,O为对角线AC的中点, ∴ AD // BC,AO=CO, ∴ ∠OAM=∠OCN,∠OMA=∠ONC, 在△AOM和△CON中, ∠OAM=∠OCN∠AMO=∠CNOAO=CO , ∴ △AOM≅△CON(AAS), ∴ AM=CN, ∵ AM // CN, ∴ 四边形ANCM为平行四边形; ∵ 在矩形ABCD中,AD=BC, 由(1)知:AM=CN, ∴ DM=BN, ∵ 四边形ANCM为平行四边形,MN⊥AC, ∴ 平行四边形ANCM为菱形, ∴ AM=AN=NC=AD-DM, ∴ 在Rt△ABN中,根据勾股定理,得 AN2=AB2+BN2, ∴ (4-DM)2=22+DM2, 解得DM=32. 25.购买一个甲种笔记本需要10元,购买一个乙种笔记本需要5元 至多需要购买21个甲种笔记本,购买两种笔记本总费用的最大值为224元 26.由题意得,点A与点B关于原点对称,即OA=OB, ∴ S△AOMS△ABE=(OAAB)2=14, 又△AEB的面积为6, ∴ S△AOM=14S△ABE=14×6=32=12|k|, ∴ k=-3,k=3(舍去), ∴ 反比例函数的关系式为y=-3x; 由k=-3可得一次函数y=-x+2,由题意得, y=-x+2y=-3x ,解得,x1=3y1=-1 ,x2=-1y2=3 , 又A在第二象限,点C在第四象限, ∴ 点A(-1, 3),点C(3, -1),(1)一次函数y=-x+2与y轴的交点N的坐标为(0, 2), ∴ S△AOC=S△CON+S△AON=12×2×(1+3)=4. 10 / 10 27.如图,连接OD, ∵ AB是直径, ∴ ∠ADB=90∘, 又∵ AB=AC, ∴ BD=CD,∠BAD=∠CAD, ∵ AO=BO,BD=CD, ∴ OD // AC, ∵ DM⊥AC, ∴ OD⊥MN, 又∵ OD是半径, ∴ MN是⊙O的切线; ∵ AB=AC, ∴ ∠ABC=∠ACB, ∵ ∠ABC+∠BAD=90∘,∠ACB+∠CDM=90∘, ∴ ∠BAD=∠CDM, ∵ ∠BDN=∠CDM, ∴ ∠BAD=∠BDN, 又∵ ∠N=∠N, ∴ △BDN∽△DAN, ∴ BNDN=DNAN, ∴ DN2=BN⋅AN=BN⋅(BN+AB)=BN⋅(BN+AC); ∵ BC=6,BD=CD, ∴ BD=CD=3, ∵ cosC=35=CDAC, ∴ AC=5, ∴ AB=5, ∴ AD=AB2-BD2=25-9=4, ∵ △BDN∽△DAN, ∴ BNDN=DNAN=BDAD=34, ∴ BN=34DN,DN=34AN, ∴ BN=34(34AN)=916AN, ∵ BN+AB=AN, ∴ 916AN+5=AN ∴ AN=807, ∴ DN=34AN=607. 10 / 10 28.把C(-1, 7),D(5, 7)代入y=ax2+bx+12, 可得a-b+12=725a+5b+12=7 , 解得a=-1b=4 , ∴ 抛物线的解析式为y=-x2+4x+12. 如图1中,过点E作EM⊥AB于M,过点D作DN⊥AB于N. 对于抛物线y=-x2+4x+12,令y=0,得到,x2-4x-12=0,解得x=-2或6, ∴ A(-2, 0),B(6, 0), ∵ D(5, 7), ∴ OA=2,DN=7,ON=5,AN=7 ∵ △CED的面积与△CAD的面积之比为1:7, ∴ DE:AD=1:7, ∴ AE:AD=6:7, ∵ EM // DN, ∵ ENDN=AMAN=AEAD=67, ∴ EM7=AM7=67, ∴ AM=EM=6, ∴ E(4, 6), ∴ 直线BE的解析式为y=-3x+18, 由y=-3x+18y=-x2+4x+12 ,解得x=6y=0 或x=1y=15 , ∴ F(1, 15), 过点P作PQ // y轴交BF于Q,设P(t, -t2+4t+12_)则Q(t, -3t+18), ∴ PQ=-t2+4t+12-(-3t+18)=-t2+7t-6, ∵ S△PBF=12⋅(-t2+7t-6)⋅5=-52(t-72)2+1258, ∵ -52<0, ∴ t=72时,△BFP的面积最大,最大值为1258. 对于抛物线y=-x2+4x+12,当y=16时,-x2+4x+12=16, 解得x1=x2=2, 当y=12时,-x2+4x+12=12,解得x=0或4, 观察图2可知:当0≤x≤2或2≤x≤4时,12≤y≤16, ∴ m=0,n=2或m=2,n=4, ∴ m-n=-2. 10 / 10查看更多