- 2021-05-12 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
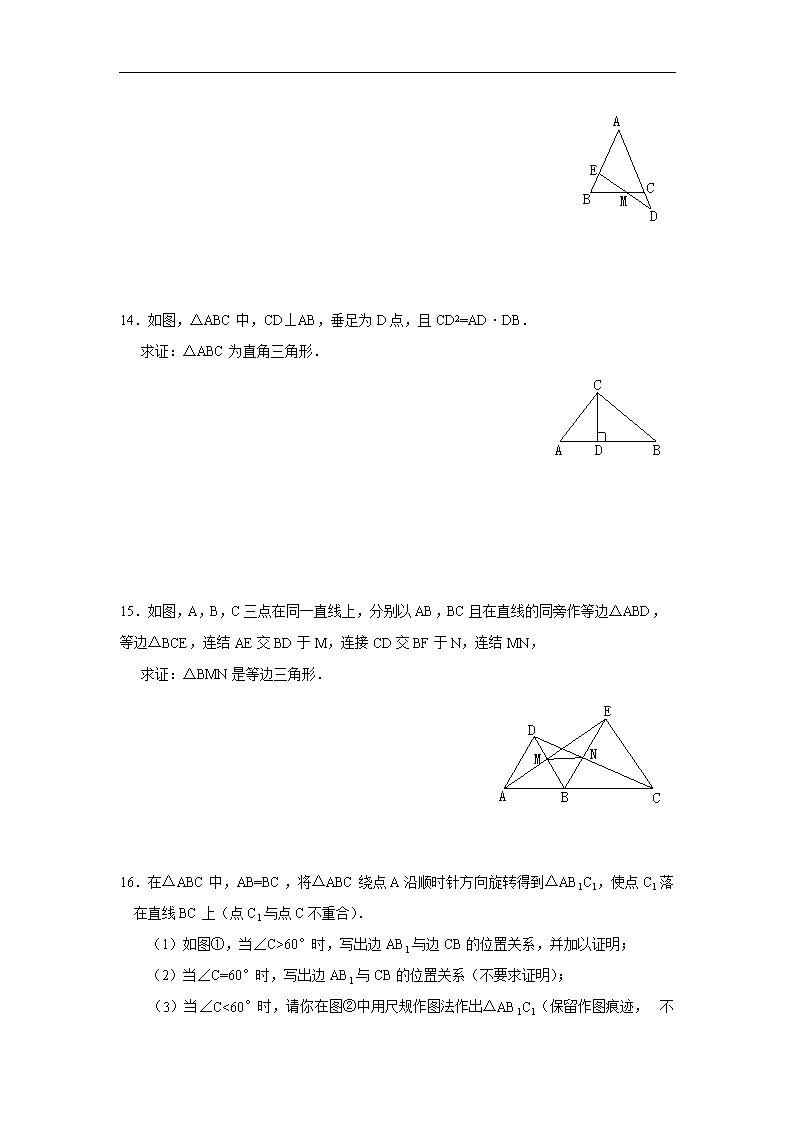
上海教育版数学七下《等腰三角形》同步练习2
14.6 等腰三角形的判定 1.如图 1,AB=AC=CD,AD=BD,图中共有_____个等腰三角形,∠B=∠C=_______度. � C � A � B � D � C � A � B � E � D � C � A � B � O � N � M (1) (2) (3) 2.如图 2,已知△ABC 的角平分线 CD 交 AB 于 D,DE∥BC 交 AC 于 E,若 DE=3,AE=4, 则 AC=________. 3.如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是________三角形. 4.△ABC 中,AD⊥BC,垂足为 D,且 BD=CD,则△ABC 的形状是_________,若使△ ABC 是等边三角形,还应补充条件_____________. 5.一个三角形的三个外角度数之比为 3:3:2,则这个三角形为( ) A.等边三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 6.如图 3,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 经过点 O,且 MN∥BC,若 BC=12,AC=18,则△AMN 的周长为( ). A.15 B.18 C.24 D.30 7.将两个全等的有一个角是 30°的直角三角形拼成如图所示,其中,两条长直角边在同一 条直线上,则图中等腰三角形的个数是( ) A.4 B.3 C.2 D.1 � 30 � 30 8.在△ABC 中,AB=12cm,AC=9cm,BC=15cm,则△ABC 的面积等于( ) A.108cm2 B.54cm2 C.180cm2 D.90cm2 9.下列说法中正确的个数有( ) ①有一个外角为 120°的等腰三角形是等边三角形 ②有两个外角相等的等腰三角形 是等边三角形 ③有三个外角都相等的三角形是等边三角形 ④有一边上的高也是这边 上的中线的等腰三角形是等边三角形 ⑤△ABC 中三边为 a,b,c,满足(a-b)(b-c) (c-a)=0,则这个三角形是等边三角形 A.1 B.2 C.3 D.4 10.已知,在△ABC 中,AB=AC,点 D、E 在边 BC 上,且 BD=CE, 求证:AD=AE. � C � A � B � E � D 11.已知如图,OA 平分∠BAC,∠1=∠2,求证:△ABC 是等腰三角形. � O � 2 � 1 � www.czsx.com.cn � C � B � A 12.如图,△ABC 中,AB=AC,D 是 AB 的中点,且 DE⊥AB,已知△BCE 的周长为 8. 且 AC-BC=2,求 AB、BC 的长. � C � A � B � E � D 13.如图△ABC 中,AB=AC,点 E 在 AB 上,点 D 在 AC 的延长线上,且 CD=EB,ED 交 BC 于 M,求证:EM=DM. � C � A � B � E � M � D 14.如图,△ABC 中,CD⊥AB,垂足为 D 点,且 CD2=AD·DB. 求证:△ABC 为直角三角形. � C � A � B � D 15.如图,A,B,C 三点在同一直线上,分别以 AB,BC 且在直线的同旁作等边△ABD, 等边△BCE,连结 AE 交 BD 于 M,连接 CD 交 BF 于 N,连结 MN, 求证:△BMN 是等边三角形. � C � A � B � E � www.czsx.com.cn � N � M � D 16.在△ABC 中,AB=BC,将△ABC 绕点 A 沿顺时针方向旋转得到△AB1C1,使点 C1 落 在直线 BC 上(点 C1 与点 C 不重合). (1)如图①,当∠C>60°时,写出边 AB1 与边 CB 的位置关系,并加以证明; (2)当∠C=60°时,写出边 AB1 与 CB 的位置关系(不要求证明); (3)当∠C<60°时,请你在图②中用尺规作图法作出△AB1C1(保留作图痕迹,不写 作法),再猜想你在(1),(2)中得出的结论是否还成立?并说明理由. 17.如图,在等边△ABC 中,D 在 BC 边上,E 在△ABC 外,∠BAD=15°, ∠DAE=70°,AD=AE,求∠CAE,∠EDC,∠EFC 的度数. 18.(1)在△ABC 中,AD⊥BC,∠B=2∠C,求证:AB+BD=CD. (2)在(1)中如果条件∠B=2∠C 与结论 AB+BD=CD 互换,仍然成立吗?试说明理由. � C � A� B � D 19.如图,△ABC 是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以 D 为顶 点作一个 60°的角,角的两边分别交 AB,AC边于 M,N 两点,连接 MN,探究:线 段 BM,MN,NC 之间的关系,并加以证明.查看更多