高中数学必修2教案：直线方程的概念与直线的斜率(共两课时)

高中数学必修2教案：直线方程的概念与直线的斜率(共两课时)

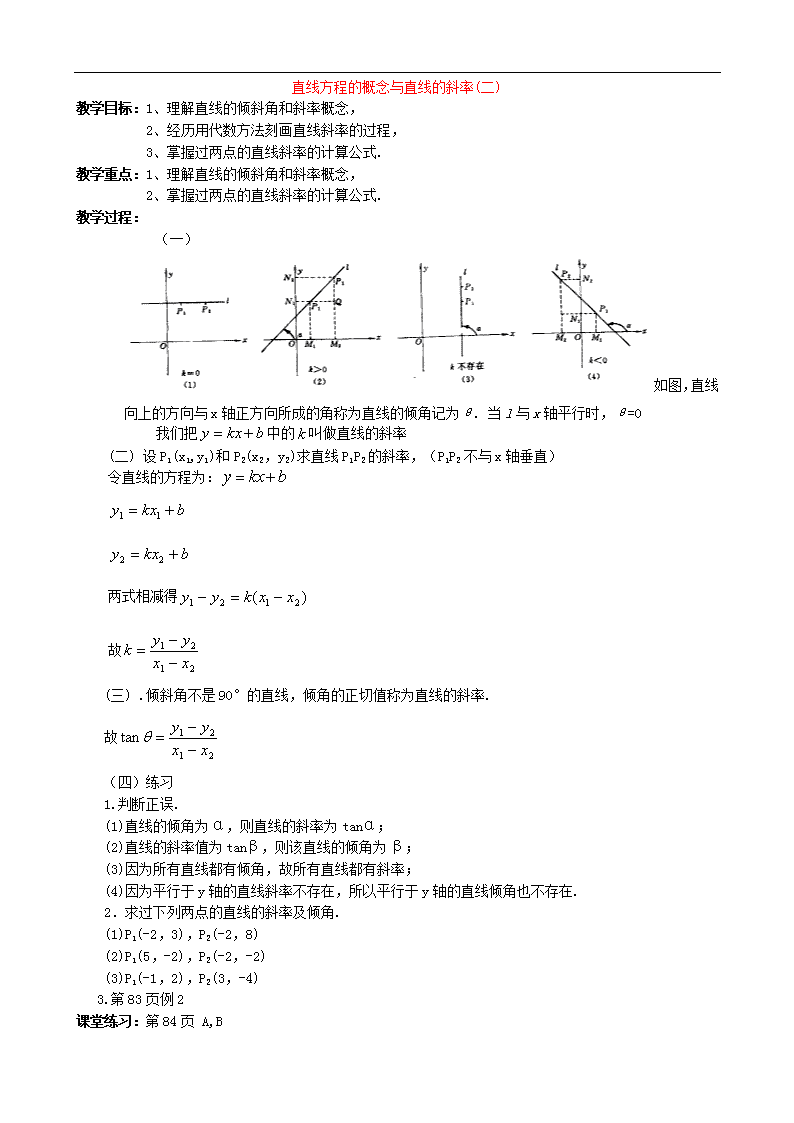
直线方程的概念与直线的斜率 教学目标：1、理解直线的方程的概念 ‎ 2、理解二元一次方程对应的是直线 教学重点：1、理解直线的方程的概念 ‎ 2、理解二元一次方程对应的是直线 教学过程：‎ ‎（一）问题1、一次函数是怎么定义的？其图象特点是什么？‎ 问题2、给定函数y = 2X+1，如何作出它的图象？‎ 问题3、已知一次函数y=2x+1，试判断点A(1，2)和点B(2，1)是否在函数图象上 判断点A在函数图象上的理论依据是：满足函数关系式的点都在函数的图象上；判断点B不在函数图象上的理论依据是：函数图象上的点的坐标应满足函数关系式．简言之，就是函数图象上的点与满足函数式的有序数对具有一一对应关系．‎ ‎(二)直线的方程 思考：直角坐标平面内，一次函数的图象都是直线吗？直线都是一次函数的图象吗？‎ 一次函数的图象是直线，直线不一定是一次函数的图象，如直线x=a连函数都不是．‎ 一次函数y=kx+b，x=a,y=c都可以看作二元一次方程，这个方程的解和它所表示的直线上的点一一对应．‎ 以一个方程的解为坐标的点都是某条直线上的点；反之，这条直线上的点的坐标都是这个方程的解．这时，这个方程就叫做这条直线的方程；这条直线就叫做这个方程的直线．‎ 上面的定义可简言之：(方程)有一个解(直线上)就有一个点；(直线上)有一个点(方程)就有一个解，即方程的解与直线上的点是一一对应的．‎ 显然，直线的方程是比一次函数包含对象更广泛的一个概念．‎ ‎(三)进一步研究直线方程的必要性 通过研究一次函数，我们对直线的方程已有了一些了解，但有些问题还没有完全解决，如y=kx+b中k的几何含意、已知直线上一点和直线的方向怎样求直线的方程、怎样通过直线的方程来研究两条直线的位置关系等都有待于我们继续研究．‎ 课堂练习：略 小结：本节课研究了直线的方程的概念 课后作业：略 直线方程的概念与直线的斜率(二)‎ 教学目标：1、理解直线的倾斜角和斜率概念，‎ ‎ 2、经历用代数方法刻画直线斜率的过程，‎ ‎ 3、掌握过两点的直线斜率的计算公式.‎ 教学重点：1、理解直线的倾斜角和斜率概念，‎ ‎ 2、掌握过两点的直线斜率的计算公式.‎ 教学过程：‎ ‎（一）如图，直线向上的方向与x轴正方向所成的角称为直线的倾角记为θ. 当l与x轴平行时，θ=0‎ 我们把中的叫做直线的斜率 ‎(二) 设P1(x1,y1)和P2(x2，y2)求直线P1P2的斜率，（P1P2不与x轴垂直）‎ 令直线的方程为：‎ 两式相减得 故 ‎(三) .倾斜角不是90°的直线，倾角的正切值称为直线的斜率.‎ 故 ‎（四）练习 ‎1.判断正误.‎ ‎(1)直线的倾角为α，则直线的斜率为tanα；‎ ‎(2)直线的斜率值为tanβ，则该直线的倾角为β；‎ ‎(3)因为所有直线都有倾角，故所有直线都有斜率；‎ ‎(4)因为平行于y轴的直线斜率不存在，所以平行于y轴的直线倾角也不存在.‎ ‎2．求过下列两点的直线的斜率及倾角.‎ ‎(1)P1(-2，3)，P2(-2，8)‎ ‎(2)P1(5，-2)，P2(-2，-2)‎ ‎(3)P1(-1，2)，P2(3，-4)‎ ‎ 3.第83页例2‎ 课堂练习：第84页 A,B 小结：通过这节课的学习，我们学习了“倾角”和“斜率”这两相概念，从“形”与“数”两方面去刻画直线相对于x轴的倾斜程度，并学习了已知两点坐标求过这两点的直线斜率的公式.‎ 课后作业：第84页习题2-2A:1‎