- 2021-05-11 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2020届一轮复习人教版整体与隔离法的综合应用学案
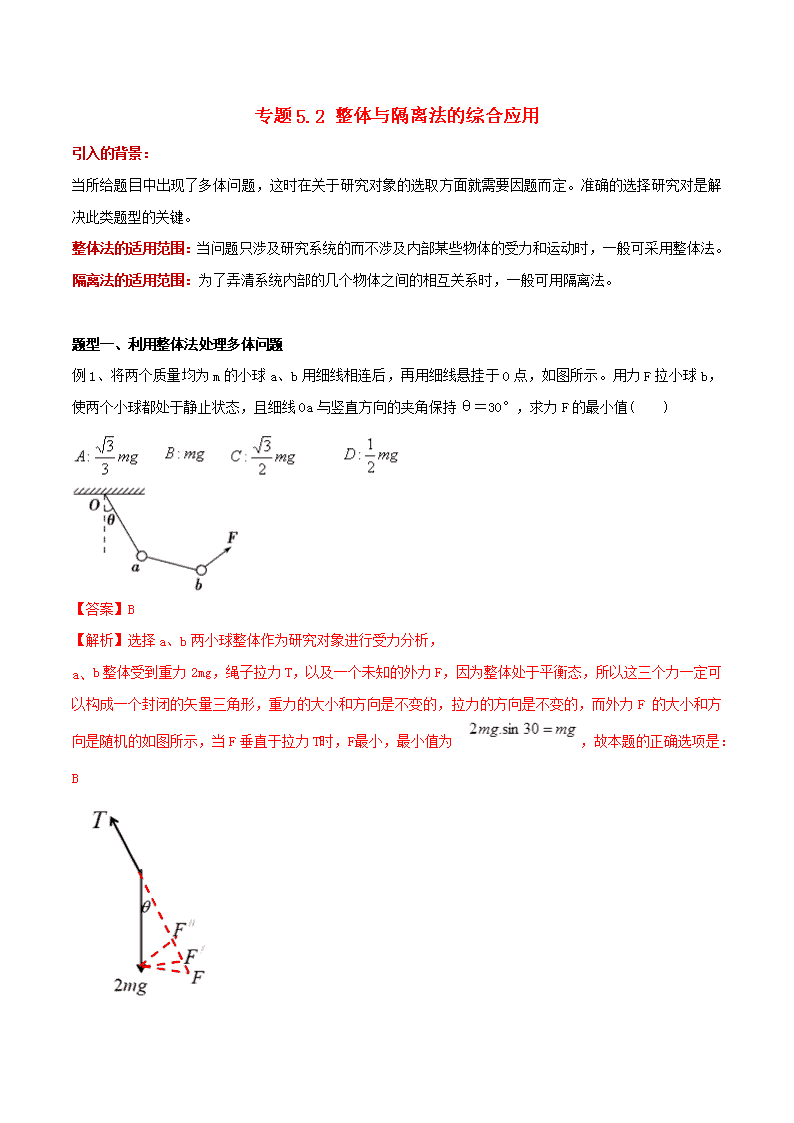
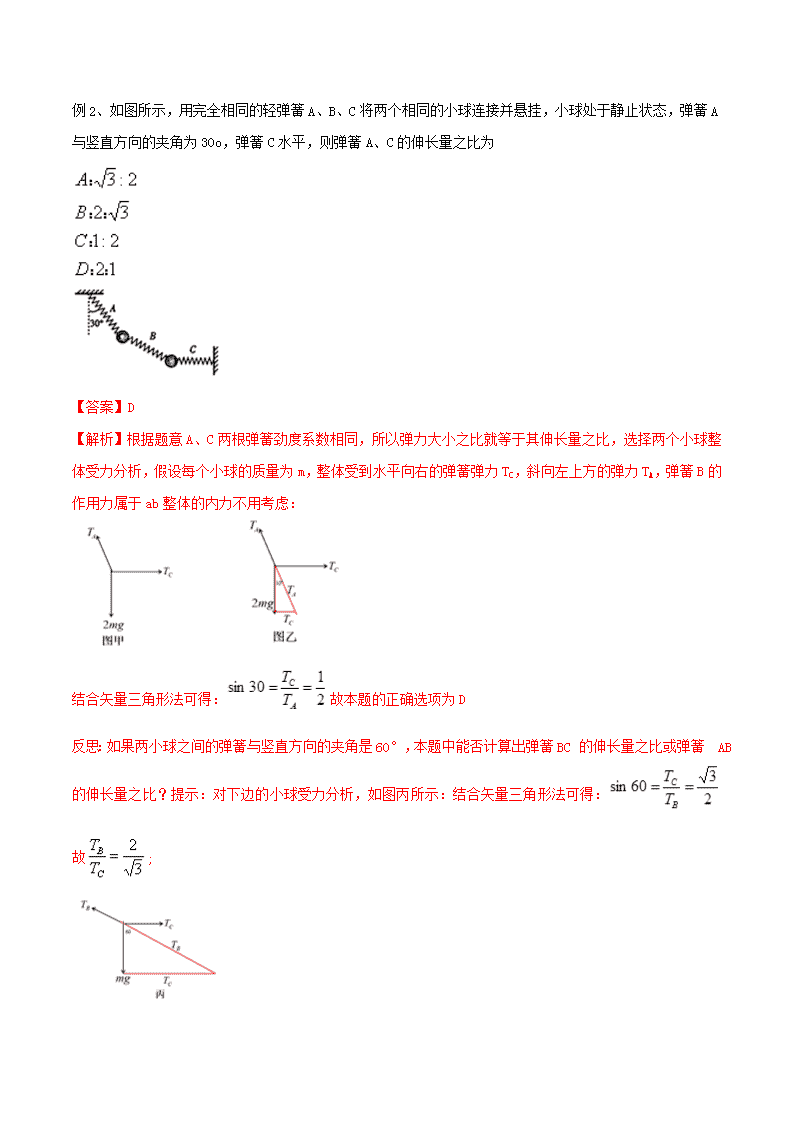
专题5.2 整体与隔离法的综合应用 引入的背景: 当所给题目中出现了多体问题,这时在关于研究对象的选取方面就需要因题而定。准确的选择研究对是解决此类题型的关键。 整体法的适用范围:当问题只涉及研究系统的而不涉及内部某些物体的受力和运动时,一般可采用整体法。 隔离法的适用范围:为了弄清系统内部的几个物体之间的相互关系时,一般可用隔离法。 题型一、利用整体法处理多体问题 例1、将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示。用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,求力F的最小值( ) 【答案】B 【解析】选择a、b两小球整体作为研究对象进行受力分析, a、 b整体受到重力2mg,绳子拉力T ,以及一个未知的外力F,因为整体处于平衡态,所以这三个力一定可以构成一个封闭的矢量三角形,重力的大小和方向是不变的,拉力的方向是不变的,而外力F 的大小和方向是随机的如图所示,当F垂直于拉力T 时,F 最小,最小值为 ,故本题的正确选项是:B 例2、如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A与竖直方向的夹角为30o,弹簧C水平,则弹簧A、C的伸长量之比为 【答案】D 【解析】根据题意A、C两根弹簧劲度系数相同,所以弹力大小之比就等于其伸长量之比,选择两个小球整体受力分析,假设每个小球的质量为m,整体受到水平向右的弹簧弹力TC,斜向左上方的弹力TA,弹簧B的作用力属于ab整体的内力不用考虑: 结合矢量三角形法可得:故本题的正确选项为D 反思:如果两小球之间的弹簧与竖直方向的夹角是60°,本题中能否计算出弹簧BC 的伸长量之比或弹簧 AB 的伸长量之比?提示:对下边的小球受力分析,如图丙所示:结合矢量三角形法可得: 故; 方法总结: 对于多体系统来说,如果问题中不涉及各组员之间的内力,只是让计算系统外力的大小关系时,可以将系统中各组员看成一个整体来进行处理,此时各组员之间的关系属于系统内力,在受力分析时不用考虑,这样可以明显简化受力分析过程,降低题目难度; 题型二、利用隔离法处理多体中组员之间的内力 例3、 一串小灯笼(五只)彼此用轻绳连接,并悬挂在空中。在稳定水平风力作用下发生倾斜,悬绳与竖直方向的夹角为30°,如图所示.设每个红灯笼的质量均为 m.则自上往下第一只灯笼对第二只灯笼的拉力大小为: 【答案】C 【解析】本题考查整体法与隔离法的综合使用,本题的关键点是要从5个小球组成的大整体中将后四个小球隔离出来,即将灯笼2、3、4、5当作一个整体;假设灯笼1、2之间的拉力大小为T,对这个整体受力分析;如图所示,结合矢量三角形法即可求得: 在右图的红色三角形中,利用矢量三角形法得: 深刻反思: 1、本题中如果要求的是第三个灯笼和第四个灯笼之间细绳的拉力,又该如何选择研究对象; 2、本题中研究对象的选择不同风力F的大小是否相同? 提示: 1、 本题中如果要求的是第三个灯笼和第四个灯笼之间细绳的拉力,可以选择第四个灯笼与第五个灯笼组成的小整体作为研究对象; 2、研究对象的选择不同,风力的大小是不同的;可以通过计算确定; 方法总结: 1、计算多体中各组员之间的内力的大小需要用到隔离法; 2、隔离法在使用时要注意两个重要的原则; ①通过隔离要使的被求的力成为隔离组员的外力; ②在选择组员进行隔离时,一定要选择受力最简单的组员进行隔离;这样被隔离的组员就不一定是一个物体,有可能是大整体中的一个小整体, 在本题中选择后4个灯笼作为研究对象正是这个道理; 易错点提示:隔离不一定是一个物体,有可能是大整体中的一个小整体; 题型三、整体与隔离法配合使用处理多体综合性问题 例4、如图所示,有5000个质量均为m的小球,将它们用长度相等的轻绳依次连接,再将其左端用细绳固定在天花板上,右端施加一水平力使全部小球静止.若连接天花板的细绳与水平方向的夹角为45°,则第2011个小球与2012个小球之间的轻绳与水平方向的夹角α的正切值等于; 【答案】A 【解析】要求得第2011个小球与2012个小球之间的轻绳与水平方向的夹角α的正切值要先求得2011与2012两个小球之间的拉力T的大小; 选择第2012-第5000个(2989个)小球作为研究对象,假设每个小球的质量为m,这2089个小球的总质量为2089m, 受力分析可知:受到重力2089mg、受到水平向右的拉力F、以及第2011与2012个小球之间的拉力T大小。 如图所示在红色的矢量三角相中可得, 如图所示选择全部5000个小球作为研究对象,小球受到重力5000mg,水平向右的拉力F,以及轻绳的拉力T, 方法总结: 整体与隔离法的引入主要是为了研究多体中各组员内力的大小关系;但是很多题目的问法非常隐蔽,像本题问的是轻绳与水平方向夹角的正切值,但是本质还是考查内力的计算问题,所以在审题时一定要准确挖掘出题目的考点是处理此类问题的关键; 例5、如图所示,两段等长细线串接着两个质量相等的小球a、b,悬挂于 O 点.现在两个小球上分别加上水平方向的外力,其中作用在 b 球上的力大小为 F、作用在 a 球上的力大小为 2F,则此装平衡时的位置可能是下列哪幅图() 【答案】C 【解析】本题的考点依然是多体问题中内力的计算,但是难点在于审题时要抓住题目涉及的隐含条件; 提示:本题的四幅区别在于细线oa与细线ab与竖直方向的夹角不同,要想比较二者的夹角大小就需要分别选择不同的研究对象进行处理;假设细线ab的与竖直方向夹角的大小为θ1,对小球b受力分析如图所示: 结合矢量三角形法可得:; 假设细线oa与竖直方向的夹角大小为θ2,拉力大小为T/选择小球ab整体进行受力分析: 结合矢量三角形法可得: 因为,所以线绳ab与竖直方向的夹角更大,故C选项正确; 反思:本题能否根据已知条件比较T与T/的大小关系? 方法总结: (1)当研究系统中只有两个组员时,题目的问题往往会针对两个组员之间的内力来发问;但是发问的方式通常比较隐蔽;像例5这样的题目就是这样的; (2)一般情况下处理多体问题时,不可能通过一步整体法或一步隔离法就能够求出结果,绝大多数的题目在处理时往往需要整体法和隔离法相互配合才能解出结果; 例6、半圆柱体M放在粗糙的水平地面上,其右端有固定放置的竖直挡板PQ,M与PQ之间放有一个光滑均匀的小圆柱体N,整个系统处于静止。如图所示是这个系统的纵截面图。若用外力F使PQ保持竖直并且缓慢地向右移动,在N落到地面以前,发现M始终保持静止。在此过程中,下列说法正确的是( ) A.地面对M的支持力不变 B.MN间的弹力先减小后增大 C.PQ对N的弹力逐渐减小 D.PQ和M对N的弹力的合力逐渐增大 E、地面对M的摩擦力逐渐增大。 【答案】AE 【解析】观察题目中的四个选项问到的问题既有M、N组成系统的外力大小的比较,也有各组员之间的内力的大小变化规律;所以本题在处理的过程中要整体与隔离法配合使用;为了研究MN之间的相互作用力FMN的的变化规律,需要隔离N,对N进行受力分析;如图所示;结合矢量三角形的动态图解法可得: 故:BC选项错误; 对M、N 整体受力分析:假设N的质量为m,M的质量为M, 例7、如图所示,水平细杆上套一细环A,环A与球B间用一轻质绳相连,质量分别为m A 、m B (m A >m B ),由于B球受到水平风力作用,A环与B球一起向左匀速运动.已知细绳与竖直方向的夹角为θ.则下列说法正确的是( ) A. 杆对A球的支持力随着风力的增加而不变 B. 环B受到的风力F为mBgtanθ C. A环与水平细杆间的动摩擦因数为mBtanθ/( mA+mB) D. 风力增大时,轻质绳对B球的拉力保持不变 E. 绳子的拉力大小为mBg/cosθ 【答案】ABE 【解析】问题中绳子的拉力属于A、B 两个小环之间的内力,小环B 比小环A 受力简单,需要隔离小环B 进行受力分析;其它的力属于系统的外力,需要对整体受力分析; 如图所示:风力增大时θ增大,重力不变,故拉力T 增大;所以:D 错E 对; 风力增大,两环的重力大小不变,杆给A 的支持力大小不变故A对; 方法总结: 整体法与隔离法解题并非绝对分开的,很多题往往需要我们整体法与隔离法交替使用。 对于隔离法来说,隔离的不一定是一个物体,有可能是从大整体中隔离出来一个小整体,也有可能是从大整体中隔离出来一个物体。 隔离的原则是: 1、要使被求的内力在隔离后变为新组员的外力; 2、在能满足条件一时,要选择受力简单的组员进行隔离。 查看更多