【物理】2019届一轮复习人教版 电场 学案

【物理】2019届一轮复习人教版 电场 学案

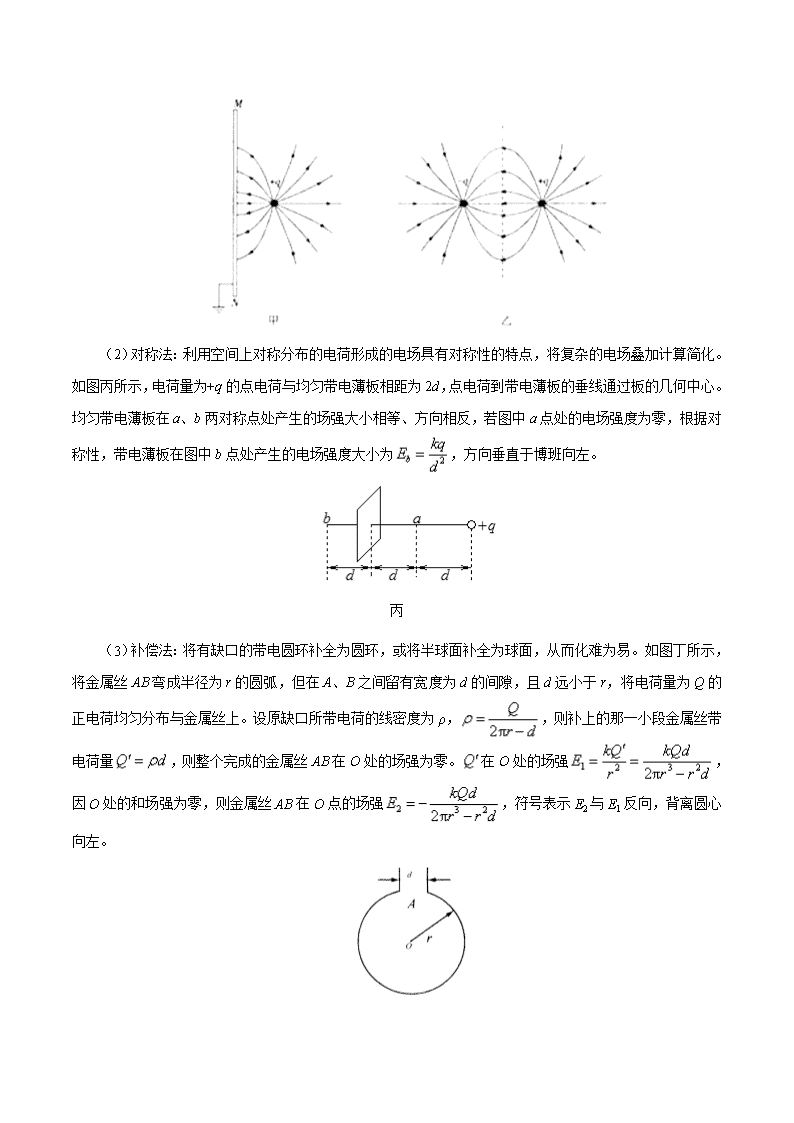
一、对静电场的基本概念和性质理解不透彻 对静电场基本概念和性质的理解易出现以下错误：‎ ‎（1）易错误地认为：场强越大的地方，电势就越高；场强的正、负和电势的正、负含义相同。不清楚场强的正、负表示方向，而电势的正、负表示大小。‎ ‎（2）易错误地认为正、负电荷在电势越高的地方，电势能都越大。‎ ‎（3）易错误地认为处于静电平衡状态的导体内部场强处处为零，电势也处处为零。‎ ‎（4）易错误地认为沿处于静电平衡状态的导体表面移动电荷时，电场力可以做功。‎ 二、对影响库仑力大小的因素理解不透彻 对库仑定律的应用易出现以下错误：‎ ‎（1）库仑定律的适用条件是真空中的点电荷，对不能看成点电荷的带电体误用库仑定律公式计算；‎ ‎（2）对不能看成点电荷的均匀带电球体也可以使用库仑定律计算库仑力的大小，但易错误地将球体表面的距离当作r代入，实际上r应为球心距离；‎ ‎（3）计算库仑力时，弄错电荷量的正负号，根据正负号确定库仑力的方向。‎ 三、不熟悉典型电场的电场线和等势线的分布 对于电场线和等势线易出现以下错误：‎ ‎（1）电场线是为了描述电场而引入的，并不是真实存在的，易错误地认为电场线是带电粒子的运动轨迹；‎ ‎（2）不明确常见的电场线和等势线的分布特点；对等量同种电荷和异种电荷在电场线上、中垂线上的场强及电势变化的规律不清楚。‎ 四、对求解电场强度的几种特殊思维方法理解不透彻 电场强度的求解方法及思路 ‎（1）等效法：在保证效果相同的前提条件下，将复杂的物理情景变换为简单的活熟悉的情景。如图甲所示，一个点电荷+q与一个很大的薄金属板形成电场，可以等效为如图乙所示的两个异种等量点电荷形成的电场。‎ ‎（2）对称法：利用空间上对称分布的电荷形成的电场具有对称性的特点，将复杂的电场叠加计算简化。如图丙所示，电荷量为+q的点电荷与均匀带电薄板相距为2d，点电荷到带电薄板的垂线通过板的几何中心。均匀带电薄板在a、b两对称点处产生的场强大小相等、方向相反，若图中a点处的电场强度为零，根据对称性，带电薄板在图中b点处产生的电场强度大小为，方向垂直于博班向左。‎ 丙 ‎（3）补偿法：将有缺口的带电圆环补全为圆环，或将半球面补全为球面，从而化难为易。如图丁所示，将金属丝AB弯成半径为r的圆弧，但在A、B之间留有宽度为d的间隙，且d远小于r，将电荷量为Q的正电荷均匀分布与金属丝上。设原缺口所带电荷的线密度为ρ，，则补上的那一小段金属丝带电荷量，则整个完成的金属丝AB在O处的场强为零。在O处的场强，因O处的和场强为零，则金属丝AB在O点的场强，符号表示E2与E1反向，背离圆心向左。‎ 丁 ‎（4）微元法：将研究对象分割成若干微小的单元，或从研究对象上选取某一“微元”加以分析，从而可以化曲为直，使变量、难以确定的量转化为常量、容易确定的量。如图戊所示，均匀带电圆环所带电荷量为Q，半径为R，圆心为O，P为垂直于圆环平面的对称轴上的一点，OP=L。设想将圆环看成n个小段组成，每一小段都可以看作点电荷，其所带电荷量，由点电荷场强公式可求得每一小段带电体在P处产生的场强为，由对称性知，各小段带电体在P处的场强E沿垂直于轴的分量Ey相互抵消，而其轴向分量Ex之和即为带电环在P处的场强EP，。‎ 戊 ‎（5）极值法：物理 中的极值问题可分为物理型和数 型两类，物理型主要依据物理概念、定理、定律求解。数 型则是根据物理规律列出方程后，依据数 中求极值的知识求解。‎ 五、电场中电势高低及电势能的判断 ‎（1）电场中电势高低的判断方法 判断角度 判断方法 依据电场线方向 沿电场线方向电势逐渐降低 依据电场力做功 根据，将WAB、q的正负号代入，由UAB的正负判断φA、φB的高低 依据场源电荷的正负 取无穷远处电势为零，正电荷周围电势为正值，负电荷周围电势为负值，靠近正电荷处电势高，靠近负电荷处电势低 依据电视能的高低 正电荷在电势较高处电视能大，负电荷在电势低处电势能大 ‎（2）电荷具有电势能大小的判断方法 判断角度 判断方法 做功判断法 电场力做正功，电视能减小；电场力做负功，电视能增加 场源电荷法 正电荷在电势高的地方电势能大，负电荷在电势低的地方电势能大 公式法 由，将q、φ的大小、正负号一起代入公式，Ep的正值越大，电势能越大；Ep的负值越小，电势能越大 能量守恒法 在电场中，若只有电场力做功时，电荷的动能和电势能相互转化，动能增加，电势能减小，反之，电势能增加 六、理不清电场中运动轨迹与电场力、电场线的关系 与电场线相关的四个易错点 ‎（1）误认为电场线方向就是电荷受到电场力作用的方向。‎ ‎（2）误认为电场线是电荷在电场中的运动轨迹；‎ ‎（3）误认为未画出电场线的地方，场强为零；‎ ‎（4）错误地根据电场线方向来判断电场强度大小，应根据电场线的疏密来判断电场强度的大小。‎ 七、不会分析电容器动态变化中的场强和电势 : ]‎ 对电容器的理解和应用易出现以下错误：‎ ‎（1）易错误地认为电容器的电容与U和Q有关；‎ ‎（2）易错误地认为充电后与电源断开的电容器，无论哪种因素变化，板间电场强度都不变；‎ ‎（3）易错误地认为电势的高低取决于板间场强的大小和与零等势面的距离大小，与哪个板接地无关。‎ 八、对带电粒子在匀强电场中偏转的特点掌握不准确 解决带电粒子在电场中运动的问题易出现以下错误：‎ ‎（1）不知道带电粒子在电场中运动时是否考虑重力，对电场力方向判断不清；‎ ‎（2）对带电粒子在电场中的运动过程分析错误；‎ ‎（3）对带电粒子经电场作用而偏转打在屏上分析时，易弄错位移的偏转角和速度的偏转角度；‎ ‎（4）对电场和重力场的复合场的分析可以用等效重力场处理，易忽视类平抛运动结论的应用。‎ 九、带电体在电场中的平衡与运动 ‎1．分析带电体平衡问题的方法 分析带电体平衡问题的方法与力 中分析物体平衡的方法是一样的，我们应 会把电 问题力 化。一般分析此问题的步骤为：‎ ‎（1）确定研究对象。如果有几个物体相互作用时，要依据题意，适当选取“整体法”或“隔离法”，一般是先整体后隔离；‎ ‎（2）对研究对象进行受力分析；‎ ‎（3）列平衡方程或根据牛顿第二定律列方程求解，经常用到动量守恒定律、动能定理等。‎ ‎2．用能量观点处理带电体在电场中的运动的方法 对于受变力作用的带电体的运动，必须借助于能量观点来处理。既是是恒力作用的问题，用能量观点处理也常常显得简捷。‎ ‎（1）用动能定理处理 思维顺序一般为 ‎①弄清研究对象，明确所研究的物理过程；‎ ‎②分析物体在所研究过程中的受力情况，弄清哪些力做功，做正功还是负功；‎ ‎③弄清所研究过程的始、末状态（主要指动能）；‎ ‎④根据W=ΔE 列出方程求解。‎ ‎（2）用能量守恒定律处理 列式的方法常有两种 ‎①由初、末状态的能量相等列方程；‎ ‎②由某种能量的减少等于另一种能量的增加列方程。‎ ‎十、静电场中涉及图象问题的处理方法 ‎1．主要类型 ‎（1）v–t图象；‎ ‎（2）φ–x图象；‎ ‎（3）E–x图象。‎ ‎2．应对策略 ‎（1）v–t图象：根据v–t图象中速度的变化、斜率的绝对值的变化（即加速度大小的变化），确定电荷所受电场力的方向与电场力的发小变化情况，进而确定电场的方向、电势的高低及电势能的变化。‎ ‎（2）φ–x图象：①电场强度的大小等于φ–x图线的斜率绝对值；②在φ–x图象中可以直接判断各点电势的大小，并可根据电势大小关系大致确定电场强度的方向；③在φ–x图象中分析电荷移动时做功的正负，可用WAB=qUAB分析WAB的正负，然后做出判断。‎ ‎（3）E–x图象：根据给出的E–x图象，确定E的方向，根据E的大小变化，确定电场的强弱分布。‎ 十一、示波管的构造和原理 ‎（1）示波管的构造：示波器的核心部件是示波管，示波管的构造简图如图所示，也可将示波管的构造大致分为三部分，即电子枪、偏转电极和荧光屏。‎ ‎（2）示波管的原理 ‎①偏转电极不加电压时，从电子枪射出的电子将沿直线运动，射到荧光屏的中心点形成一个亮斑。‎ ‎②在（或）加电压时，则电子被加速，偏转后射到（或）所在直线上某一点，形成一个亮斑（不在中心）。当两偏转电极均加电压时，两个方向都有偏转位移，根据运动的独立性，X方向的位移取决于上的电压，Y方向的位移取决于上的电压，利用带电粒子在电场中运动的分析方法求解。‎ ‎（3）示波管实际工作时，竖直偏转板和水平偏转板都加上电压。一般加在竖直偏转板上的电压是要研究的信号电压，加大水平偏转板上的扫描电压，若两者周期相同，在荧光屏上就会显示信号电压随时间变化的波形图。‎ 水平面上有一边长为L的正方形，其a、b、c三个顶点上分别固定了三个等量的正点电荷Q，将一个电荷量为+q的点电荷分别放在正方形中心点O点和正方形的另一个顶点d点处，两处相比，下列说法正确的是 A．q在d点所受的电场力较大 B．q在d点所具有的电势能较大 C．d点的电势高于O点的电势 D．q在两点所受的电场力方向相同 对于场强的比较，不少同 由对称性直接得出a、b、c、d四点的相关物理量的关系，而忽视了题中给出的是a、b、c三个顶点上分别固定了三个等量的正点电荷Q，并不是在O点固定一个点电荷。‎ 由点电荷的电场及场的叠加可知，在O点b、c两处的点电荷产生的电场相互抵消，O点处的场强等于a处点电荷所产生的场强，即，方向由a指向O；而在d点处 ‎1．如图所示，A、B、C、D、E是半径为r的圆周上等间距的五个点，在这些点上各固定一个点电荷，除A点处的电荷量为–q外，其余各点处的电荷量均为+q，则圆心O处 A．场强大小为方向沿OA方向 B．场强大小为方向沿AO方向 C．场强大小为方向沿OA方向 D．场强大小为方向沿AO方向 ‎【答案】C 大小为故O点的合场强为A点–q在O点产生的场强与B、C、D、E四个+q。 ‎ 如图所示，Q为固定的正点电荷，A、B两点位于Q的正上方和Q相距分别为h和0.25h，将另一点电荷从A点由静止释放，运动到B点时速度刚好又变为零。若此电荷在A点处的加速度大小为‎3g/4，则此电荷在B点处的加速度a为 A．a=‎4g，方向竖直向上 B．a=‎4g，方向竖直向下 C．a=‎3g，方向竖直向上 D．a=‎3g，方向竖直向下 没有对两点电荷相互作用即运动全面分析，主观认为A向下运动，则两点电荷距离减小，所受库仑力增大，加速度增大。 ‎ 对点电荷在A点进行受力分析，得到，则，点电荷在 ‎1．如图所示，一个均匀的带电圆环，带电量为+Q，半径为R，放在绝缘水平桌面上。圆心为O点，放O点做一竖直线，在此线上取一点A，使A到O点的距离为R，在A点放一检验电荷+q，则+q在A点所受的电场力为 A．，方向向上 ‎ B．，方向向上 C．，方向水平向左 D．不能确定 ‎【答案】B 如图所示为一空腔导体周围的电场线分布图，电场方向如图中箭头所示，M、N、P、Q是以O为圆心的一个圆周上的四点，其中M、N在一条直电场线上，P、Q在一条曲电场线上，则有 A．M点的电场强度比N点的电场强度大 B．P点的电势比Q点的电势低 C．负电荷在P点的电势能小于其在Q点的电势能 D．M、O间的电势差等于O、N间的电势差 不清楚无论导体带电与否，经典平衡时表面为等势面，不会运用电场的基本性质进行解题。‎ 由电场线的疏密程度表示电场的强弱，所以N点的场强比M点的场强大，故A错误；沿着电场线的方向电势越来越低，所以Q点的电势比P点的电势低，故B错误；负电荷由P点运动到Q点，电场力左负功，电势能增加，所以负电荷在P点时的电势能小于在Q点时的电势能，故C正确；根据电场分布可以知道，MO间的平均电场强度比ON之间的平均电场强度小，故由公式可知，MO间的电势差小于ON间的电势差，故D错误。答案：C。 ‎ ‎1．如图所示，在两个点电荷Q1、Q2产生的电场中，实线为其电场线分布，虚线为电子（不计重力）从A点运动到B点的运动轨迹，则下列判断正确的是 A．电子经过A点的加速度比经过B点的加速度大 B．Q1的电荷量大于Q2的电荷量 C．电子在A点的电势能大于在B点的电势能 D．两个点电荷连线中点O的场强为零 ‎【答案】A ‎ [ : ]‎ 如图所示，真空中Ox坐标轴上的某点有一个点电荷Q，坐标轴上A、B两点的坐标分别为‎0.2 m和‎0.7 m。在A点放一个带正电的试探电荷，在B点放一个带负电的试探电荷，A、B两点的试探电荷受到电场力的方向都跟x轴正方向相同，电场力的大小F跟试探电荷电荷量q的关系分别如图中直线a、b所示。下列说法正确的是 A．B点的电场强度的大小为0.25 N/C B．A点的电场强度的方向沿x轴负方向 C．点电荷Q是正电荷 D．点电荷Q的位置坐标为‎0.3 m 不能正确分析受力与电场强度的关系而导致本题错解。‎ 由两试探电荷受力情况可知，点电荷Q为负电荷，且放置于A、B两点之间某位置，选项B、C均错；设Q与A点之间的距离为l，则点电荷在A点产生的场强为EA= Q/l2=Fa/qa=4×105 N/C，同理，点电荷在B点产生的场强为EB= Q/(0.5–l)2=Fb/qb=0.25×105 N/C，解得l=0.1 m，所以点电荷Q的位置坐标为xQ=xA+l=0.2+0.1=0.3 (m)，所以选项A错误，选项D正确。答案：D。 ‎ ‎1．空间中P、Q两点处各固定一个点电荷，其中P点处为正电荷，P、Q两点附近电场的等势面分布如图所示，a、b、c、d为电场中的4个点，则 A．P、Q两点处的电荷等量同种 B．a点和b点的电场强度相同 C．c点的电势低于d点的电势 D．负电荷从a到c，电势能减少 ‎【答案】D 两个固定的等量异号点电荷所产生电场的等势面如图中虚线所示，一带负电的粒子以某一速度从图中A点沿图示方向进入电场在纸面内飞行，最后离开电场，粒子只受静电力作用，则粒子在电场中 A．做直线运动，电势能先变小后变大 B．做曲线运动，电势能先变小后变大 C．做直线运动，电势能先变大后变小 D．做曲线运动，电势能先变大后变小 不能充分利用等势面判断电势的高低，从而确定带电体运动后电势的高低。‎ ‎1．如图所示，真空中有一个固定的点电荷，电荷量为+Q。图中的虚线表示该点电荷形成的电场中的四个等势面。有两个一价离子M、N（不计重力，也不计它们之间的电场力）先后从a点以相同的速率v0射入该电场，运动轨迹分别为曲线apb和aqc，其中p、q分别是它们离固定点电荷最近的位置。①M一定是正离子，N一定是负离子。②M在p点的速率一定大于N在q点的速率。③M在b点的速率一定大于N在c点的速率。④M从p→b过程电势能的增量一定小于N从a→q电势能的增量。以上说法中正确的是 A．只有①③ B．只有②④‎ C．只有①④ D．只有②③‎ ‎【答案】B ‎【解析】①由图可知电荷N受到中心电荷的斥力，而电荷M受到中心电荷的引力，故两粒子的电性一定不同。由于中心电荷为正电，则M一定是负离子，N一定是正离子，故①错误；②由图可判定M电荷在运动过程中，电场力做正功，导致动能增加；而N电荷在运动过程中，电场力做负功，导致动能减小。所以在p点的速率一定大于N在q点的速率，故②正确；③D由于abc三点在同一等势面上，故粒子M在从a向b运动过程中电场力所做的总功为0，N粒子在从a向c运动过程中电场力所做的总功为0。由于两粒子以相同的速率从a点飞入电场故两粒子的分别经过b、c两点时的速率一定相等，故③错误。④由图可知N粒子在从a向q运动过程中电场力做负功的值大于粒子M在从p向b运动过程中电场力做负功的值，故M从p→b过程电势能的增量一定小于N从a→q电势能的增量，故④正确。故选B 一匀强电场的方向平行于xOy平面，平面内a、b、c三点的位置如图所示，三点的电势分别为10 V、17 V、26 V。下列说法不正确的是 A．电场强度的大小为2.5 V/cm B．坐标原点处的电势为1 V C．电子在a点的电势能比在b点的低7 eV D．电子从b点运动到c点，电场力做功为9 eV 不能对图象作出正确分析导致本题错误。‎ 根据匀强电场的电场强度公式，结合电势差与场强间距，即可求解；依据电势差等于电势之差；根据电场力做功表达式，从而确定电场力做功，同时也能确定电势能的变化情况。如图所示，在ac连线上，确定一b′点，电势为17 V，将bb′连线，即为等势线，那么垂直bb′连线，则为电场线，再依据沿着电场线方向，电势降低，则电场线方向如图，因为匀强电场，则有，依据几何关系，则，因此电场强度大小为，故A正确；根据，因a、b、c三点电势分别为，解得：原点处的电势为，故B正确；因，电子从a点到b点电场力做功为，因电场力做正功，则电势能减小，那么电子在a点的电势能比在b点的高7 eV，C错误；，电子从b点运动到c点，电场力做功为，D正确。答案：C。 ‎ ‎1．‎ 如图所示，虚线表示等势面，相邻两等势面的电势差相等，有一带正电的小球在电场中运动，实线表示该带正电荷的小球的运动轨迹，小球在a点的动能为20 eV，运动到b点的动能为2 eV。若取c点零电势点，则当这个小球的电势能为–6 eV时它的动能为（不计重力和空气阻力作用）‎ A．16 eV B．14 eV C．6 eV D．4 eV ‎【答案】B 某同 在研究电子在电场中的运动时，得到了电子由a点运动到b点的轨迹（图中实线所示），图中未标明方向的一组虚线可能是电场线，也可能是等势面，则下列说法正确的判断是 A．如果图中虚线是电场线，电子在a点动能较大 B．如果图中虚线是等势面，电子在b点动能较小 C．不论图中虚线是电场线还是等势面，a点的场强都大于b点的场强 D．不论图中虚线是电场线还是等势面，a点的电势都高于b点的电势 错误地将粒子运动的规矩理解为等势线或者其他物理量导致本题错解。‎ 若虚线是电场线，从轨迹弯曲方向可知电场力沿着电场线向左，ab 曲线上每一点的瞬时速度与电场力方向均成钝角，故电子做减速运动，动能减小，在a处动能最大，所以A正确；若虚线为等势面，[ : XX ]‎ ‎1．某静电场的电场线如图中实线所示，虚线是某个带电粒子仅受电场力作用的运动轨迹，以下说法正确的是 A．粒子一定带负电荷 B．粒子在M点的加速度小于它在N点的加速度 C．粒子在M点的电势能小于它在N点的电势能 D．M点的电势小于N点的电势 ‎【答案】B ‎【解析】由电荷的运动轨迹可知，电荷的受力沿着电场线的方向，所以电荷为正电荷，所以A错误。电 ‎【名师点睛】电场线密的地方电场的强度大，电场线疏的地方电场的强度小，电场力做正功，电势能减小，电场力做负功，电势能增加．沿着电场线方向电势降低。 ‎ 两个较大的平行板A、B相距为d，分别接在电压为U的电源正负极上，开关S闭合时质量为m ‎，带电量为–q的油滴恰好静止在两板之间，如图所示，在保持其他条件不变的情况下，将两板非常缓慢地水平错开一些，以下说法正确的是 A．油滴将向上运动，电流计中的电流从b流向a B．油滴将下运动，电流计中的电流从a流向b C．油滴静止不动，电流计中的电流从a流向b D．油滴静止不动，电流计中无电流流过 不能正确理解电容器极板变化接电源与不接电源板间电场强度变化的区别而导致本题错解。‎ 将两板缓慢地错开一些，两板正对面积减小，根据电容的决定式得知，电容减小，而电压不变，则由知，电容器带电量减小，电容器处于放电状态，电路中产生顺时针方向的电流，则电流计中有a→b的电流。由于电容器板间电压和距离不变，则由，知板间场强不变，油滴所受电场力不变，仍处于静止状态。故C正确。ABD错误。答案：C。‎ ‎1．如图所示，A、B是两块平行金属极板，充电后与电源断开。A板带正电，B板带负电并与地连接，有一带电微粒悬浮在两板间P点处静止不动。现将B板上移到虚线处，则下列说法正确的是 A．带电微粒的电性为正 B．平行板电容器电容增大 C．极板间P点的电势升高 D．带电微粒的电势能增大 ‎【答案】BD 如图所示，O1O2为带电平行板电容器的中轴线，三个相同的带电粒子沿O1O2射入两板间。粒子1打到B板的中点，粒子2刚好打在B板边缘，粒子3从两板间飞出，设三个粒子只受电场力作用，则 A．三个粒子在电场中运动的时间关系为t1t3‎ C．三个粒子进入电场的初速度关系为v1=v2=v3‎ D．三个粒子在电场中运动过程的动能变化量关系为ΔE 1>ΔE 2>ΔE 3‎ 不明白电容器极板间为匀强电场导致本题错解。‎ 三个粒子都在电场中做类平抛运动，沿O1O2方向做匀速直线运动，沿电场方向做匀加速直线运动，则有x=v0t，y=at2，a=，粒子在电场中运动的时间t=，正比于，故可得t1=t2>t3，A错误，B正确；粒子进入电场的初速度v0=，正比于，故可得v1ΔE 3，D错误。答案：B。 ‎ ‎1．如图所示，在真空中有一水平放置的不带电平行电容器，板间距为d，电容为C，上板B接地，现有大量质量均为m、带电荷量为q 的小油滴，以相同的初速度持续不断地从两板正中间沿途中虚线方向射入，第一滴油滴正好落到下板A的正中央P点，如果能落到A板的油滴仅有N滴，且第滴油滴刚好能飞离电场，假设落到A板的油滴的电荷量能被板全部吸收，不考虑油滴间的相互作用，重力加速度为g，则下列说法不正确的是 A．落到A板的油滴数 B．落到A板的油滴数 C．第滴油经过电场的整个过程中所增加的动能为 D．第滴油经过电场的整个过程中所减少的机械能为 ‎【答案】B ‎【解析】第一滴油滴正好落到下板A的正中央P点，则：，y=gt12，设以上述速度入射的带电粒子，最多能有n个落到下极板上。则第（N+1）个粒子的加速度为a，由牛顿运动定律得：mg–qE=ma；其中：得：，第（N+1）粒子做匀变速曲线运动，竖直 ‎【名师点睛】考查如何处理平抛运动的思路，掌握运动的合成与分解的方法，理解运动 ‎ 公式与牛顿第二定律的综合应用。‎ 在竖直平面内有水平向右、场强为的匀强电场。在场中有一根长为的绝缘细线，一端固定在点，另一端系一个质量为的带电小球，它静止时细线与竖直方向成角。如图所示，给小球一个初速度让小球恰能绕点在竖直平面内做圆周运动，取小球在最初静止时的位置为电势能和重力势能的零点，，求：‎ ‎（1）小球所带电荷量；‎ ‎（2）小球恰能做圆周运动的动能最小值；‎ ‎（3）小球恰能做圆周运动的机械能最小值。‎ 不能将重力和电场力等效为重力场进行解题导致本题错误。‎ ‎（1）根据平衡关系：‎ 得到 代入数据得 ‎（2）由于重力和电场力都是恒力，所以它们的合力也是恒力，类比重力场，在圆上各点中，小球在平衡位置A时动能最大，在平衡位置A的对称点B，小球的动能最小，在对称点B，小球受到的重力和电场力，其合力F作为小球做圆周运动的向心力，而绳的拉力恰为零。‎ 有，而 所以 ‎（3）当小球在圆上最左侧的C点时，电势最高，电势能最大，机械能最小。由B运动到A ‎，根据动能定理，有 ‎1．如图所示，在竖直平面内有水平向右、场强为E=1×104 N/C的匀强电场。在匀强电场中有一根长L=2 m的绝缘细线，一端固定在O点，另一端系一个质量为0.08 g的带电小球，它静止时悬线与竖直方向成37°角，若小球获得初速度恰能绕O点在竖直平面内做圆周运动，取小球在静止时的位置为电势能零点和重力势能零点，cos 37°=0.8，g取10 m/s2。下列说法正确 A．小球的带电荷量q=6×10–5 C B．小球动能的最小值为1 J C．小球在运动至圆周轨迹上的最高点时有机械能的最小值 D．小球绕O点在竖直平面内做圆周运动的电势能和机械能之和保持不变，且为4 J ‎【答案】AB ‎【解析】对小球进行受力分析如图甲所示，可得：，解得小球的带电荷量为：，故A正确；由于重力和电场力都是恒力，所以它们的合力也是恒力，在圆上各点中，小球在平衡位置A点时的势能（重力势能和电势能之和）最小，在平衡位置的对称点B点，小球的势能最大，由于小球总能量不变，所以在B点的动能E B最小，对应速度vB最小，在B点，小球受到的重力和电场力，其合力作为小球做圆周运动的向心力，而绳的拉力恰为零，有：，而，所以，故B正确；由于总能量保持不变，即恒量，所以当小球在圆上最左侧的C点时，电势能 最大，机械能最小，故C错误；由于总能量保持不变，即恒量，由B运动到A，，，所以，总能量，故D错误。‎ 甲 乙 ‎【名师点睛】关键抓住小球恰好做圆周运动，求出等效最高点的临界速度，根据该功能关系确定何处机械能最小，知道在等效最高点的动能最小，则重力势能和电势能之和最大。‎ 用一条绝缘轻绳悬挂一个带电小球，小球质量为1.0×10–2 g，所带电荷量为+2.0×10–8 C。现加一水平方向的匀强电场，平衡时绝缘轻绳与竖直方向成30°角（如图所示）。求这个匀强电场的电场强度（g取10 N/ g）。‎ 错误地认为，带电体在电场中只能运动，不能平衡，导致本题误以为无解。‎ 取带电小球为研究对象，小球在三个共点力作用下处于平衡状态，受力分析如图所示 ‎[ : |xx| ]‎ ‎【名师点睛】本题是带电体在电场中平衡问题，当作力 问题去处理，关键是分析电场力大小和方向。‎ ‎1．如图所示，一带电量为–q、质量为m小球用绝缘细线悬挂于O点，并置于水平方向的匀强电场中，静止时细线与竖直方向的夹角为θ，则该匀强电场的大小为______，方向______。‎ ‎【答案】 水平向右 ‎【解析】小球受力如图所示，根据平衡条件可知：电场力与重力的合力与细线的拉力T等值、方向反向，则力的合成图得知：‎ ‎，解得：，小球带负电，电场力方向水平向左，所以电场强度方向水平向右。 ‎ 两个等量同种电荷固定于光滑水平面上，其连线中垂线上有A、B、C三点，如图甲所示。一个电荷量为2 C，质量为1 g的小物块从C点静止释放，其运动的vt图象如图乙所示，其中B点处为整条图线切线斜率最大的位置（图中标出了该切线）。则下列说法正确的 A．B点为中垂线上电场强度最大的点，场强E=2 V/m B．由C到A的过程中物块的电势能先减小后变大 C．由C点到A点的过程中，电势逐渐升高 D．AB两点电势差UAB=–5 V 不能正确将v–t图象与电场相关知识结合导致本题错解。‎ 两个等量的同种正电荷，其连线中垂线上电场强度方向由O点沿中垂线指向无穷远；电荷量为2 C仅在运动方向上受电场力作用从C点到B、到A运动的过程中，根据v–t图可知在B点的加速度为运动物体先做加速度增大后做加速度减小的加速运动，则判断电荷所受电场力大小变化情况和加速度变化情况。速 ‎1．M、N是某电场中一条电场线上的两点，若在M点释放一个初速度为零的电子，电子仅受电场力作用，并沿电场线由M点运动到N点，其电势能Ep随位移x变化的关系如图所示，其中电子在M点时的电势能为EpM，电子在N点时的电势能为EpN，则下列说法正确的是 A．电子在N点时的动能小于在M点的动能 B．该电场有可能是匀强电场 C．该电子运动的加速度越来越小 D．电子运动的轨迹为曲线 ‎【答案】C 率在减小，所以电场力在减小，电场强度在减小，加速度在减小，故B错误、C正确；带电粒子初速度为零，且沿着电场线运动，其轨迹一定为直线，故D错误。 ‎ 示波器可以用来观察电信号随时间变化的情况，其核心部件是示波管，其原理图如下，为水平偏转电极，为竖直偏转电极。以下说法正确的是 A．加图3波形电压、不加信号电压，屏上在两个位置出现亮点 B．加图2波形电压、加图1波形电压，屏上将出现两条竖直亮线 C．加图4波形电压、加图2波形电压，屏上将出现一条竖直亮线 D．加图4波形电压、加图3波形电压，屏上将出现图1所示图线 不明白示波管的工作原理及构造导致本题错解。‎ 加图3波形电压、不加信号电压，则电子将在两个不同方向的电压一定的电场中运动发生两个大小相同方向相反的位移，故在屏上水平方向的两个位置出现亮点，选项A正确；加图2波形电压、加图1波形电压，屏上将出现一条竖直亮线，选项B错误；加图4波形电压、加 ‎1．示波器的核心部件是示波管，下图是它的原理图。如果在偏转电极之间和偏转电极之间都没加电压，电子束从电子枪射出后沿直线传播，打在荧光屏中心，从右向左观察，在那里产生一个亮斑。‎ ‎（1）如果在电极之间不加电压，但在之间加不变的电压，使的电势比高（即正负），则电子打在荧光屏上的位置位于__________上（填、、或，是荧光屏中心）；当所加电压增大时，电子打在荧光屏上的位置将__________。（填“上移”、“下移”或“不变”）‎ ‎（2）如果在之间加正弦电压，如图甲所示，而在电极之间加随时间线性变化的电压，如乙图所示，则荧光屏上看到的图形是丙图中的__________。‎ ‎ ‎ A． B．‎ C． D．‎ ‎【答案】（1）OY 上移 （2）A ‎【解析】（1）电子带负电，受到的电场力方向与电场方向相反，所以在电极之间不加电压，但在之间加不变的电压，使的电势比高（即正负）时，粒子将受到向上的电场力，故粒子向上偏转，将打在OY上；间电压增大，则电子的偏转距离增大，所以应上移；‎ ‎（2）电子在荧光屏偏转的距离与偏转电压成正比，则在偏转电极YY′上加按正弦规律变化的电压，电子在荧光屏偏转的距离按正弦规律变化，而在偏转电极XX′上加图乙所示的扫描电压，水平方向电子不断从右向左匀速扫描，在荧光屏上出现一条正弦曲线，A正确。‎ ‎1．电势与电场强度的深入理解 电势具有相对意义，理论上可以任意选取零电势点（面），因此电势与场强没有直接关系，但有一点要记住：沿电场线方向电势降低，因此离正电荷越近，电势越高，离负电荷越近，电势越低；电荷在电场中某点具有的电势能，由该点的电势与电荷的电荷量（包括电性）的乘积决定，即，与电势一样具有相对性，对于正、负电荷，电场力做功等于电荷电势能的减少量，即，可以借此来判断电荷电势能的变化，比较同一电荷在电场中不同点电势能的大小。‎ 电场强度是矢量，计算非点电荷在某点产生的电场强度，要“先分后合”，先将非点电荷“微分”为很多点电荷，计算各个点电荷在该点产生的场强，然后求出这些场强的矢量和。如果非点电荷对称分布，注意利用对称性简化计算。‎ 习惯：在讨论电场力的性质时，计算中只代入量值计算大小，方向由电性直接判断；而在讨论电场的性质时，计算要同时代入表示电性、电势高低及电势差的正、负号，因为此时的“+”、“–”‎ 跟量值的大小有关。‎ ‎2．电势高低的判断方法 ‎（1）沿电场线方向，电势越来越低，电场线由电势高的等势面指向电势低的等势面。‎ ‎（2）判断出UAB的正负，再由比较φA、φB的大小，若UAB>0，则φA>φB；若UAB<0，则φA、φB。‎ ‎（3）取无穷远处为电势零点，正电荷周围电势为正值，且离正电荷近处电势高；负电荷周围电势为负值，且离负电荷近处电势低。‎ ‎3．由运动的轨迹判断电场的性质应注意的问题 ‎（1）从轨迹弯曲方向判断受力方向（说明：粒子受力方向一定沿电场线指向轨迹凹侧），从而分析电场方向或电荷的正负；‎ ‎（2）结合带电粒子速度方向与电场力的方向，确定电场力做功的正负（说明：若速度方向与电场力方向夹角小于90°，电场力做正功；若夹角大于90°，电场力做负功），从而确定电势能、电势的变化等。‎ ‎4．运用电容的定义式和决定式分析电容器相关量变化的思路 ‎（1）确定不变量，分析是电压不变还是所带电荷量不变。‎ ‎①电容器充电后仍与电源联通，且电路中各电阻值均不变，电容器两端电压U不变；‎ ‎②当电容器充电后与电源断开，且没有除电容器外的其他元件与电容器构成回路时，电容器带电量Q不变。‎ ‎（2）用决定式分析平行板电容器电容的变化。‎ ‎（3）用定义式分析电容器所带电荷量或两极板间电压的变化。‎ ‎（4）用和分析电容器极板间场强的变化。‎ ‎（5）用来确定电容器间某点A的电势高低及变化（其中UAO为A点到零电势点间的电势差，dAO为A点到零等势面间的距离）。‎ ‎1．如图所示，a、b是两个点电荷，它们的电荷量分别为Q1、Q2，MN是ab连线的中垂线，P是中垂线上的一点。下列哪种情况能使P点电场强度方向指向MN的右侧 A．Q1、Q2都是正电荷，且Q1|Q2|‎ C．Q1是负电荷，Q2是正电荷，且|Q1||Q2|‎ ‎【答案】B 的右侧，故B正确。‎ ‎2．如图所示，两个带电金属小球中心距离为r，所带电荷量相等为Q，则关于它们之间电荷的相互作用力大小F的说法正确的 A．若是同种电荷， B．若是异种电荷，‎ C．若是同种电荷， D．不论是何种电荷，‎ ‎【答案】AB ‎【解析】净电荷只能分布在金属球的外表面，若是同种电荷则互相排斥，电荷间的距离大于r，如图所示，根据库仑定律，它们之间的相互作用力小于。若是异种电荷则相互吸引，电荷间的距离小于r，则相互作用力大于，故选项A、B正确。‎ 布在两球较远离的球面处，如图所示，则有。‎ ‎3．A、B两个点电荷在真空中所产生电场的电场线（方向未标出）如图所示。图中C点为两点电荷连线的中点，MN为两点电荷连线的中垂线，D为中垂线上的一点，电场线的分布关于MN左右对称。则下列说法中正确的是 A．这两点电荷一定是等量异种电荷 B．这两点电荷一定等量同种电荷[ : XX ]‎ C．DC两点的电势不一定相等 D．正电荷在C点的电势能比D点大 ‎【答案】A ‎【名师点睛】常见电场的电场线分布及等势面的分布要求我们能熟练掌握，并要注意沿电场线的方向电势是降低的，同时注意等量异号电荷形成电场的对称性。‎ ‎4．如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，半径为R，将等电荷量的两正点电荷Q放在圆周上，它们的位置关于AC对称，与O点的连线和OC间夹角为30°，下列说法正确的是 A．O点的电场强度大小为 B．O点的电场强度大小为 C．电荷q从A点运动到C点，电场力做的总功为零 D．电荷q从B点运动到D点，电场力做的总功为正 ‎【答案】B ‎【解析】作出两个电荷在O处的场强，及沿AC间的电场线，如图所示。根据场强公式可得：，根据矢量三角形可得O处的合场为：，故A错误，B正确；根据对称性可知，C点与E点的电势相等，而E点的电势高于A点的电势，则C点的电势高于A点的电势，所以电荷q从A点运动到C点，电场力做功不为零，故C错误；根据对称性可知，B点与D点的电势相等，其电势差为零，则电荷q从B点运动到D点，电场力做功为零，故D错误。‎ ‎5．图中、和分别表示点电荷的电场的三个等势面，它们的电势分别为、和。一质子（）从等势面上某处由静止释放，仅受电场力作用而运动，已知它经过等势面时的速率为，则对质子的运动判断正确的是 A．质子从等势面运动到等势面电势能增加 B．质子从等势面运动到等势面动能增加 C．质子经过等势面时的速率为 D．质子经过等势面时的速率为 ‎【答案】B ‎【解析】由运动到，则电场力做功为正功，则电势能减小，动能增加．故A错误，B正确。由到，；由到，；联立得：，故CD错误。 ‎ ‎6．如图所示，一带电液滴在重力和匀强电场对它的作用力的作用下，从静止开始由b沿直线运动到d，且bd与竖直方向所夹的锐角为45°，则下列结论中不正确的是 A．此液滴带负电 B．液滴做匀加速直线运动 C．合外力对液滴做的总功等于零 D．液滴的电势能减少 ‎【答案】C ‎【名师点睛】解决本题的关键知道当物体所受的合力与速度的方向在同一条直线上时，物体做直线运动。以及知道电场力做正功，电势能减小，电场力做负功，电势能增加。‎ ‎7．图中虚线是某电场中的一簇等势线。两个带电粒子从P点均沿等势线的切线方向射入电场，粒子运动的部分轨迹如图中实线所示。若粒子仅受电场力的作用，下列说法中正确的是 A．a、b两点的电场强度大小关系Ea>Eb B．a、b两点的电势关系一定有：Ua>Ub C．粒子从P运动到a的过程中，电势能增大 D．粒子从P运动到b的过程中，动能增大 ‎【答案】D 受到中心电荷的引力，电场力对b粒子做正功，动能增大，D正确。‎ ‎8．如图所示，M、N是两块水平放置的平行金属板，R0为定值电阻，R1和R2为可变电阻，开关S闭合。质量为m的带正电荷的微粒从P点以水平速度v0射入金属板间，沿曲线打在N板上的O点。若经下列调整后，微粒仍从P点以水平速度v0射入，则关于微粒打在N板上的位置说法正确的是 A．保持开关S闭合，增大R1，粒子打在O点左侧 B．保持开关S闭合，增大R2，粒子打在O点左侧 C．断开开关S，M极板稍微上移，粒子打在O点右侧 D．断开开关S，N极板稍微下移，粒子打在O点右侧 ‎【答案】A ‎【解析】保持开关S闭合，由串并联电压关系可知，R0两端的电压为，增大R1，U将减小，电容器两端的电压减小，故粒子受重力和电场力，产生的加速度增大，平行板两极板电压减小达到极板上则，水平位移为，水平位移将减小，故粒子打在O点左侧侧，故A正确；保持开关S闭合，增大R2，不会影响电阻R两端的电压，故粒子打在O点，故B错误；断开开关，平行板带电量不变，平行板间的电场强度为，结合及可得，电场强度不变，故加速度不变，M极板稍微上移，不会影响离子的运动，故还打在O点，故C错误；断开开关，平行板带电量不变，平行板间的电场强度为，结合及可得，电场强度不变，加速度不变，M极板稍微下移，不会影响离子的运动，故还打在O点，故D错误。‎ ‎【名师点睛】本题关键分析电容器的电压是否变化。当断开开关S，改变板间距离时，板间场强不变，油滴也保持不动。 ‎ ‎9．如图所示，一价氢离子（11H）和二价氦离子（24He）的混合体，经同一加速电场加速后，垂直射入同一偏转电场中，偏转后，打在同一荧光屏上，则它们 A．同时到达屏上同一点 B．先后到达屏上同一点 C．同时到达屏上不同点 D．先后到达屏上不同点 ‎【答案】B ‎【名师点睛】解决本题的关键知道带电粒子在加速电场和偏转电场中的运动情况，知道从静止开始经过同一加速电场加速，垂直打入偏转电场，运动轨迹相同。做选择题时，这个结论可直接运用。‎ ‎10．在x轴上有两个点电荷q1、q2，其静电场的电势φ在x轴上分布如图所示。下列说法正确有 A．q1和q2带有异种电荷 B．x1处的电场强度为零 C．负电荷从x1移到x2，电势能减小 D．负电荷从x1移到x2，受到的电场力增大 ‎【答案】AC 所以D错误。 …… ‎ ‎11．如图所示，光滑斜面倾角为37°，一带有正电的小物块质量为m，电荷量为q，置于斜面上，当沿水平方向加有如图所示的匀强电场时，带电小物块恰好静止在斜面上，求电场强度为多大？‎ ‎【答案】‎ ‎【解析】对小物块受力分析如图所示，物块静止于斜面上，则 mgsin 37°=qEcos 37°‎ ‎12．如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接，在过圆心O的水平界面MN的下方分布有水平向右的匀强电场。现有一质量为m、电荷量为+q的小球从水平轨道上A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场（P点恰好在A点的正上方，如图所示，小球可视为质点，小球运动到C点之前电荷量保持不变，经过C点后电荷量立即变为零）。已知A、B间距离为2R，重力加速度为g，在上述运动过程中，求：‎ ‎（1）小球经过C点的速度大小；‎ ‎（2）小球经过半圆轨道上与圆心O等高处D点的速度大小；‎ ‎（3）电场强度E的大小；‎ ‎（4）小球在圆轨道上运动时的最大速率。‎ ‎【答案】（1） （2） （3） （4）‎ ‎（3）小球从A到D由动能定理有：qE∙3R–mgR=mvD2‎ 得：‎ ‎（4）设小球运动到圆轨道F点时速度最大，设最大速度为v，此时OF与竖直线OB夹角设为α，小球从A点运动到F点的过程，根据动能定理知 qE(2R+Rsin α)–mgR(1–cos α)=mv2‎ 即mv2=mgR(sin α+cos α+1)‎ 根据数 知识可知，当α=45°时动能最大 由此可得 ‎13．示波管是示波器的核心部件，它由电子枪、偏转电极和荧光屏组成，一束电子流经加速电压加速后，沿中线进入平行板偏转电场，经电场偏转后打在荧光屏上。如图所示。已知两偏转电场极板长均为，极板间距均为d=1.0 cm。水平偏转电场极板边缘距荧光屏距离为。不计竖直偏转电极与水平偏转电极间间隙。请回答或求下列问题：‎ ‎（1）如果亮斑出现在荧光屏上如图所示位置，那么示波管中的极板X、Y应带什么电？‎ ‎（2）电子流的偏移量和打在荧光屏位置是通过调节加速电压和偏转电压来实现的，要使电子流能进入水平偏转电场中。竖直偏转电压与加速电压的比值不能超过多大？‎ ‎（3）如果加速电压，偏转电压，偏转电压，求电子在荧光屏上的水平偏移量 ‎【答案】（1）X、Y极板均带正电 （2） （3）‎ 由类平抛运动的规律得：水平方向，竖直方向，‎ 联立解得：②‎ 联立①②得：‎ 要使电子进入水平偏转电场，则竖直偏转量最大值 代入数值得：，即 ‎（3）由题知：，，‎ 则在水平电场的偏移量：‎ 代入数值得：‎ 由于没有竖直偏移，则电子流象从水平偏转电场极板中点直线射向荧光屏一样。‎ 所以由几何关系求得电子在荧光屏上水平偏移量 代入数值得：‎