2021届高考数学一轮复习第六章不等式第2讲一元二次不等式及其解法课件

2021届高考数学一轮复习第六章不等式第2讲一元二次不等式及其解法课件

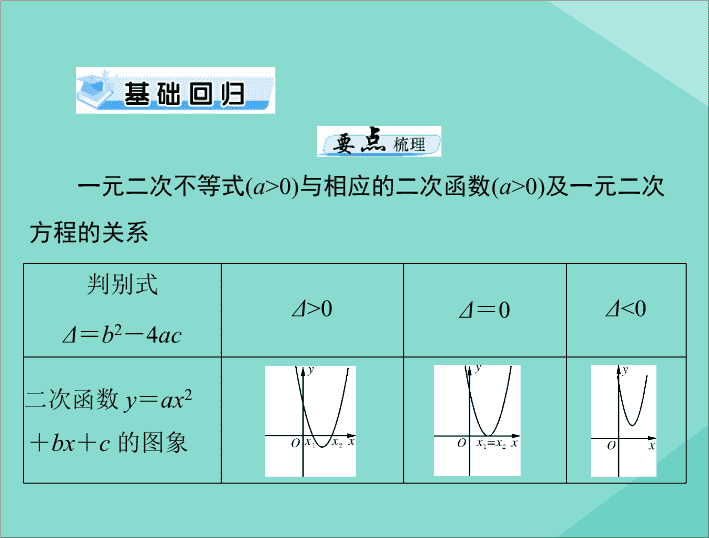
第2讲 一元二次不等式及其解法 课标要求 考情风向标 1.经历从实际情境中抽象出 一元二次不等式模型的过程. 2.通过函数图象了解一元二 次不等式与相应函数、方程的 联系. 3.会解一元二次不等式，对给 定的一元二次不等式，尝试设 计求解的程序框图 1.不等式解法是不等式中的重要 内容，它的应用范围几乎涉及高 中数学的所有章节，且常考常新， “三个二次”之间的联系的综合 应用等问题是高考的热点. 2.由于本节内容涉及的计算较 多，因此学习时应注意运算能力 的训练 判别式 Δ ＝ b 2 －4 ac Δ >0 Δ ＝0 Δ <0 二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象 一元二次不等式 ( a >0) 与相应的二次函数 ( a >0)及一元二次 方程的关系 判别式 Δ ＝ b 2 －4 ac Δ >0 Δ ＝0 Δ <0 一元二次方程 ax 2 ＋ bx ＋ c ＝0 的根 有两相异实根 x 1,2 ＝_____________ 有两相同实根 没有 实根 ax 2 ＋ bx ＋ c >0 的 解集 { x | x < x 1 或 x > x 2 } R ax 2 ＋ bx ＋ c <0 的 解集 { x | x 1 < x < x 2 } ∅ ______ (续表) ∅ 1.设集合 A ＝{ x | x 2 －4 x ＋3<0}， B ＝{ x |2 x －3>0}，则 A ∩ B ＝( ) D 2.已知不等式 ax 2 ＋ bx ＋2>0 的解集为{ x |－1< x <2}，则不等 式 2 x 2 ＋ bx ＋ a <0 的解集为( ) A 3.(2018 年新课标Ⅰ ) 已知集合 A ＝ { x | x 2 － x －2>0}，则 ∁ R A ＝( B ) A.{ x |－1< x <2} B.{ x |－1≤ x ≤2} C.{ x | x <－1}∪{ x | x >2} D.{ x | x ≤－1}∪{ x | x ≥2} 4.(2019 年天津 ) 设 x ∈ R ，使不等式 3 x 2 ＋ x －2<0 成立的 x 的取值范围为__________. 考点 1 解一元二次、分式不等式 A.{ x |－2＜ x ＜－1} C.{ x |0＜ x ＜1} B.{ x |－1＜ x ＜0} D.{ x | x ＞1} 解析： 由 x ( x ＋2)＞0 得 x ＞0 或 x ＜－2；由| x |＜1 得－1＜ x ＜1， ∴不等式组的解集为{ x |0＜ x ＜1}.故选 C. 答案： C 答案： B (3)(2019 年上海 ) 不等式 | x ＋1| <5 的解集为________. 解析： 由 | x ＋1|<5 得 －5 < x ＋1<5，即－6< x <4. 答案： (－6,4) 答案： C 【规律方法】 解一元二次不等式的一般步骤： ①化：把不等式变形为二次项系数大于零的标准形式； ②判：计算对应方程的判别式； ③求：求出对应的一元二次方程的根，或根据判别式说明 方程有没有实根； ④写：利用 “ 大于取两边，小于取中间 ”写出不等式的解 集. 例 2 ： (1) 解关于 x 的不等式 x 2 －( a ＋1) x ＋ a <0； (2)解关于 x 的不等式 ax 2 －( a ＋1) x ＋1<0； (3)解关于 x 的不等式 x 2 －2 ax ＋2≤0( a ∈ R )； (4)解关于 x 的不等式： ax 2 －2≥2 x － ax ( a ∈ R ). 解： (1) 原不等式可化为( x － a )( x －1)<0. 当 a >1 时，原不等式的解集为(1， a )； 当 a ＝1 时，原不等式的解集为 ∅ ； 当 a <1 时，原不等式的解集为( a, 1). 考点 2 含参数不等式的解法 【规律方法】 解含参数的有理不等式时分以下几种情况讨 论： ①根据二次项系数讨论 ( 大于 0 ，小于 0 ，等于 0)； ②根据根的判别式讨论( Δ >0 ， Δ ＝ 0 ， Δ <0)； ③根据根的大小讨论( x 1 > x 2 ， x 1 ＝ x 2 ， x 1 < x 2 ). 考点 3 一元二次不等式的应用 例 3 ： 已知 f ( x )＝ ax 2 ＋ bx ＋ c 的图象过点(－1,0)，是否存在 解： ∵ f ( x )的图象过点(－1,0)， ∴ a － b ＋ c ＝0. ① ∴当 x ＝1 时也成立，即 1≤ a ＋ b ＋ c ≤1. 【规律方法】 赋值法 ( 特殊值法 )可以使“探索性”问题变 得比 较明朗，是解决这类问题比较常用的方法 . 【跟踪训练】 1.对于函数 f ( x )，若 f ( x 0 )＝ x 0 ，则称( x 0 ， x 0 )是函数 f ( x )的不 动点. (1)已知函数 f ( x )＝ ax 2 ＋ bx － b 有两个不动点(1,1)和(－3， －3)，求 a ， b 的值； (2)若对于任意实数 b ，函数 f ( x )＝ ax 2 ＋ bx － b 总有两个相异 的不动点，求实数 a 的取值范围. ∴ a ＝1， b ＝3. (2)∵ f ( x )＝ ax 2 ＋ bx － b 有两个相异的不动点， ∴ ax 2 ＋ bx － b ＝ x 有两个相异的解. ∴ ax 2 ＋( b －1) x － b ＝0 有两个相异的解. ∴ Δ ＝( b －1) 2 ＋4 ab >0 对任意的实数 b 都成立. ∴ b 2 ＋(4 a －2) b ＋1>0 对任意的实数 b 都成立. ∴(4 a －2) 2 －4<0.∴0< a <1. 思想与方法 ⊙利用转化与化归思想求解一元二次不等式恒成立问题 例题： 已知 f ( x )＝ mx 2 － mx －1. (1)若对于 x ∈ R ， f ( x )<0 恒成立，求实数 m 的取值范围； (2)若对于 x ∈[1,3]， f ( x )<－ m ＋5 恒成立，求实数 m 的取值 范围； (3)若对于| m |≤1， f ( x )<0 恒成立，求实数 x 的取值范围. (2) 在给定某区间上恒成立 . ①当 x ∈ [ m ， n ] ， f ( x ) ＝ ax 2 ＋ bx ＋ c ≥0 恒成立，结合图象， 只需 f ( x ) min ≥0 即可； ②当 x ∈ [ m ， n ] ， f ( x ) ＝ ax 2 ＋ bx ＋ c ≤0 恒成立，只需 f ( x ) max ≤0 即可 . (3) 解决恒成立问题一定要搞清谁是自变量，谁是参数 .一般 地，知道谁的取值范围，谁就是自变量，求谁 的取值范围，谁 就是参数 . 如第 (1)(2) 小问中 x 为变量 ( 关于 x 的二次函数 ) ， m 为 参数. 第 (3) 小问中 m 为变量 ( 关于 m 的一次函数 ) ， x 为参数 . 【跟踪训练】 2.(2019 年陕西通州模拟 ) 若关于 x 的不等式 x 2 ＋2 a x ＋1≥0 在[0，＋∞)上恒成立，则实数 a 的取值范围为( ) A.(0，＋∞) C.[－1,1] B.[－1，＋∞) D.[0，＋∞) 方法二，设 f ( x )＝ x 2 ＋2 ax ＋1，函数图象的对称轴为直线 x ＝－ a .当－ a ≤0，即 a ≥0 时， f (0)＝1>0，∴当 x ∈[0，＋∞) 时， f ( x )≥0 恒成立；当－ a >0，即 a <0 时，要使 f ( x )≥0 在[0， ＋ ∞) 上恒成立 ， 需 f ( － a ) ＝ a 2 －2 a 2 ＋1 ＝－ a 2 ＋1≥0，得 －1≤ a <0.综上，实数 a 的取值范围为[－1，＋∞). 答案： B 3.(2019 年江西八校联考 ) 若对任意的 m ∈[－1,1]，函数 f ( x ) ＝ x 2 ＋( m －4) x ＋4－2 m 的值恒大于零，则 x 的取值范围是( ) B A.(1,3) C.(1,2) B.(－∞，1)∪(3，＋∞) D.(－∞，1)∪(2，＋∞) 解析： f ( x )＝ x 2 ＋( m －4) x ＋4－2 m ＝( x －2) m ＋ x 2 －4 x ＋4.当 x ＝2 时， f ( x )＝0，不符合题意；当 x >2 时，( x －2)·(－1)＋ x 2 － 4 x ＋4>0，得 x >3；当 x <2 时，( x －2)·1＋ x 2 －4 x ＋4>0，得 x <1. 综上， x <1 或 x >3.故选 B. 解决一元二次不等式有关问题的常见数学思想方法. (1)数形结合思想：“三个二次”的完美结合是数形结合思 想的具体体现. (2)分类讨论思想：当二次项系数含参数 a 时，要对二次项 系数分 a ＞0、 a ＜0 和 a ＝0 三种情况讨论；对方程根的情况进 行分类讨论( Δ ＞0， Δ ＝0， Δ ＜0)；如果根里含有参数，要注意 对两个根的大小进行讨论. (3)转化与化归思想：解分式、指数、对数、绝对值等类型 的不等式时，一般要把它们转化成一元二次(一次)不等式(组) 的形式进行解决.转化的方法通常是代数化、有理化、整式化、 低次化.