七年级上数学课件- 4-3-3 余角和补角 课件（24张）_人教新课标

七年级上数学课件- 4-3-3 余角和补角 课件（24张）_人教新课标

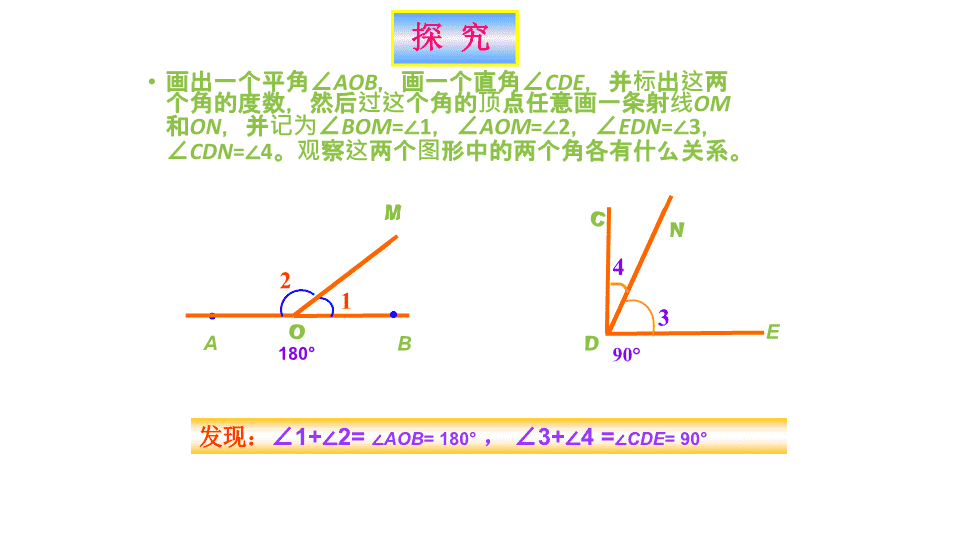
4.3.3 4 • 画出一个平角∠AOB，画一个直角∠CDE，并标出这两 个角的度数，然后过这个角的顶点任意画一条射线OM 和ON，并记为∠BOM=∠1，∠AOM=∠2，∠EDN=∠3， ∠CDN=∠4。观察这两个图形中的两个角各有什么关 系。 2 1 M 180° 90° C E N 3 A BO·· · D 动动手，画一画。 90° E N D 3 • 画出一个平角∠AOB，画一个直角∠CDE，并标出这两 个角的度数，然后过这个角的顶点任意画一条射线OM 和ON，并记为∠BOM=∠1，∠AOM=∠2，∠EDN=∠3， ∠CDN=∠4。观察这两个图形中的两个角各有什么关 系。 探 究 1 BO M ·· 180°A 2 4 C 发现：∠1+∠2= ∠AOB= 180° ， ∠3+∠4 =∠CDE= 90° 如果两个角的和等于90° (直角)，就说这两 个角 互为余角 (complementary angle) 简称“互余” 其中每一个角是另一个角的余角。 9 0      如 果   那 么 与 互 余 反之也成立 注： 只有锐角有余角 如果两个角的和等于180° (平角)，就说这 两个角 互为补角 (supplementary angle) 简称“互 补” 其中每一个角是另一个角的补角。 1 8 0     如 果   那 么 与 互 补 反之也成立 （1）定义中的“互为”一词如何理解？ （2）互补、互余的两角是否一定有公共顶点或公共边？ （3）∠1 + ∠2 + ∠3 = 180°,能说∠1 、∠2、 ∠3 互补吗？ 提问答疑，理解定义 2）若∠1与∠2互补，则∠1+ ∠2=________. 3) ∠1= 180°- ∠2,则∠1与∠2的关系为___________. 180° 互为补角 1、抢答 三、反馈练习 余角 ∠α ∠α 的余角 ∠α 的补角 30° 42° 54° 62°23′ 二、看谁答得快 60 ° 150 ° 48 ° 138 ° 36 ° 126 ° 27 ° 37 ′ 117 ° 37 ′ x 90 x  180 x  从上表中你可以得到什么结论？ 锐角的补角比它的余角大90度 [来源:Zxxk.Com] 解： 设这个角的度数为x度， 由题意得： (180- x)+20=3x 答 ： 这 个 角 为 5 0 50x 解得 3 2.已知 ：一个角的补角加上20 后等于这个角 余角 的 倍。 求： 这 角 个 (180- ) 20 3(90 )x x  设这个角的度数为x度 1、已知：一个锐角的补角加上 后等于 求：这个角的度数 20 这个角的三倍 2 （ (2)图中∠α的余角∠1，∠2的大小有什么关系？ 为什么？ (3) 这一结论用文字怎么叙述？ 同 角的余角相等 1= 2 所以 1= 2 所以 1=90 - 2= 90 -     因为 ； A (等) α 2 β 1 1 1= 90 - 2= 90 -     因为 ； 又因为∠α=∠β (1) 动手画一画： 已知∠α(如图)，请利用三角板 画的∠α的余角 C O B α（ D 同 角的补角相等(等) C O B α 1A D 2 1 3 2 4 (2) 动手画一画 已知∠α(如图)， 请利用三角板画的∠α的补角 [来源:Zxxk.Com] 已知∠1与∠2互补，∠3 与∠4互补。若∠1=∠3， 说说∠2和∠4有什么关系？ 由∠1与∠2互补，∴ ∠2= 180°－ ∠1 由∠3与∠4互补，∴ ∠4= 180°－ ∠3 又因为∠1=∠3， 180°－ ∠1=180°－ ∠3 所以∠2=∠4 推导性质 1 2 3 4 练习： （1）若∠1与∠2互余， ∠2与∠3互余， 则 ___________，根据___________. （2）若∠1与∠2互补， ∠2与∠3互补， 则___________，根据___________. ∠1= ∠3 同角的余角相等 ∠1= ∠3 同角的补角相等 余角和补角 1.(2012·长沙中考)下列四个角中，最有可能与70°角互补的 是( ) 【解析】选D.因为互补的两角之和是180°，所以70°角的补 角应大于90°，故选D. 2.下列图形中，∠1和∠2互为余角的是( ) 【解析】选D.选项A中的两角和的度数不能确定，选项B中∠1 和∠2互补，选项C中∠1和∠2相等，选项D中∠1和∠2互余. 3.(2011·广州中考)已知∠α=26°,则∠α的补角是____度. 【解析】因为∠α=26°,所以∠α的补角是180°-26°=154°. 答案：154 4.∠A与∠B互补，∠B与∠C互补，∠C=80°，则∠A的度数是 ________. 【解析】因为同角的补角相等，所以∠A=∠C=80°. 答案:80° 5.∠A的余角和它的补角之比是1∶3，求∠A的度数. 【解析】设∠A的度数为x°，则180-x=3(90-x)， 解得x=45.所以∠A的度数是45°. 例 如图，A，O，B在同一直线上,射 线OD和射线OE分别平分∠AOC和 ∠BOC，图中哪些角互为余角？ 推导性质，理解运用 推导性质，理解运用 所以∠COD +∠COE＝ ∠AOC+ ∠BOC 解：因为A，O，B在同一直线上, 所以∠AOC和∠BOC互为补 角. 又因为射线OD和射线OE 分别平分∠AOC∠BOC， 2 1 2 1 ＝ (∠AOC+ ∠BOC)2 1 ＝90° 所以， ∠COD 和∠COE互为余角， 同理， ∠AOD +∠BOE， ∠AOD +∠COE ， ∠COD +∠BOE也互为余角. 练习： 6.如图，O是直线AB上的点， OC是∠AOB的平分线，OD是一条射线， ∠AOD的补角是 ，余角是_______. 【解析】因为OC是∠AOB的平分线， 所以∠AOC=∠BOC=90°， 则∠AOD的补角是∠BOD，余角是∠COD. 答案:∠BOD　　　∠COD 课堂小结 •本节课学习了余角和补角， 并通过简单的推理，得出 了余角和补角的性质。 同 （等） 角的余角相等 同 （等）角的补角相等 作业 P139 2. 3. 4 再 见