中考图形变换知识点总结

中考图形变换知识点总结

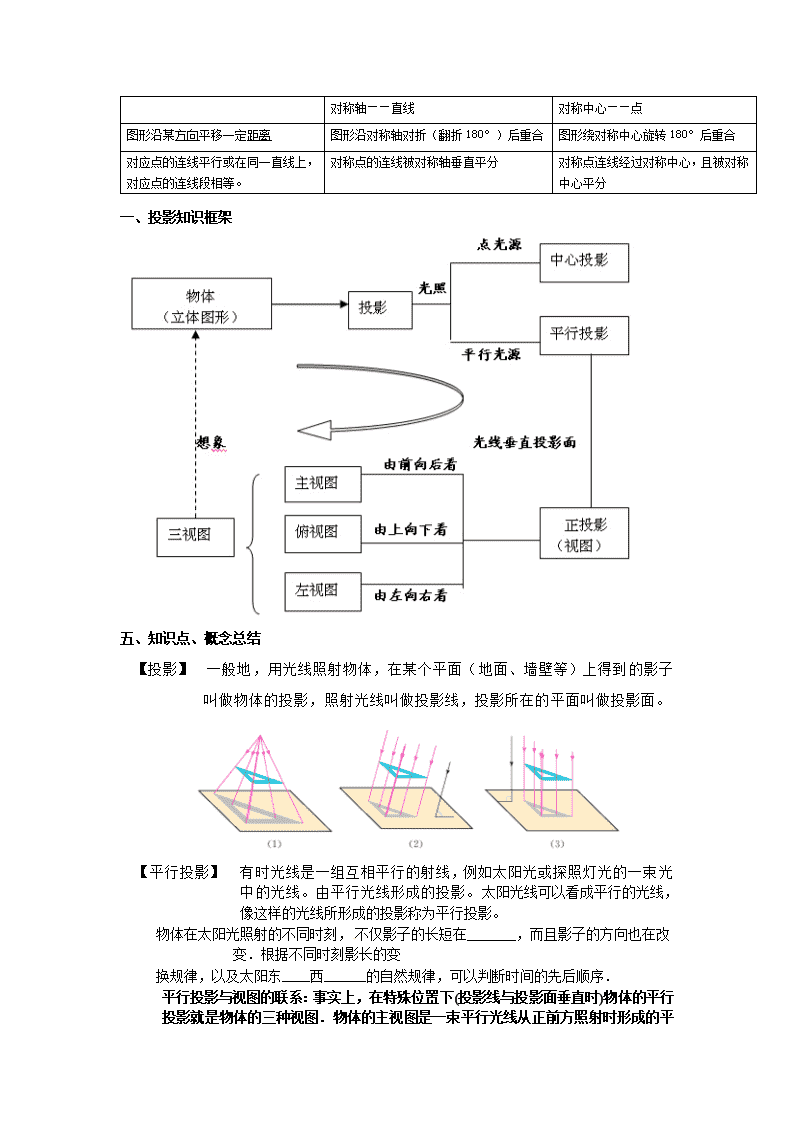
中考图形变换知识点总结 ‎ ‎ ‎[轴对称图形] ‎ ‎ 如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴．毛 ‎ 有的轴对称图形的对称轴不止一条，如圆就有无数条对称轴．‎ ‎[轴对称] ‎ 有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称． [图形轴对称的性质]‎ 如果两个图形成轴对称，那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线．‎ ‎[轴对称与轴对称图形的区别]‎ 轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．‎ ‎[线段的垂直平分线]‎ ‎ （1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）．‎ ‎ （2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．‎ ‎ [轴对称变换]‎ 由一个平面图形得到它的轴对称图形叫做轴对称变换．‎ 成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到．‎ ‎[轴对称变换的性质]‎ ‎ （1）经过轴对称变换得到的图形与原图形的形状、大小完全一样 ‎ （2）经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点．‎ ‎ （3）连接任意一对对应点的线段被对称轴垂直平分．‎ ‎[作一个图形关于某条直线的轴对称图形]‎ ‎ （1）作出一些关键点或特殊点的对称点．‎ ‎（2）按原图形的连接方式连接所得到的对称点，即得到原图形的轴对称图形．‎ 二．中心对称 ‎1．中心对称的有关概念：中心对称、对称中心、对称点 ‎ 把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么称这两个图形关于这点对称，也称这两个图形成中心对称，这个点叫做对称中心，两个图形中的对应点叫做对称点。‎ ‎2．中心对称的基本性质：‎ ‎（1）成中心对称的两个图形具有图形旋转的一切性质。‎ ‎（2）成中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。 ‎ 三．中心对称图形 ‎1．中心对称图形的有关概念：中心对称图形、对称中心 ‎ 把一个平面图形绕某一点旋转180°，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。这个点就是它的对称中心。‎ ‎2．中心对称与中心对称图形的区别与联系 ‎ 如果将成中心对称的两个图形看成一个图形，那么这个整体就是中心对称图形；反过来，如果把一个中心对称图形沿着过对称中心的任一条直线分成两个图形，那么这两个图形成中心对称。‎ ‎3．图形的平移、轴对称（折叠）、中心对称（旋转）的对比 图形的平移 轴对称（图形）‎ 中心对称（图形）‎ 对称轴——直线 对称中心——点 图形沿某方向平移一定距离 图形沿对称轴对折（翻折180°）后重合 图形绕对称中心旋转180°后重合 对应点的连线平行或在同一直线上，对应点的连线段相等。‎ 对称点的连线被对称轴垂直平分 对称点连线经过对称中心，且被对称中心平分 一、投影知识框架 五、知识点、概念总结 ‎【投影】　一般地，用光线照射物体，在某个平面（地面、墙壁等）上得到的影子叫做物体的投影，照射光线叫做投影线，投影所在的平面叫做投影面。‎ ‎ ‎ ‎【平行投影】　有时光线是一组互相平行的射线，例如太阳光或探照灯光的一束光中的光线。由平行光线形成的投影。太阳光线可以看成平行的光线，像这样的光线所形成的投影称为平行投影。‎ ‎ 物体在太阳光照射的不同时刻，不仅影子的长短在_______，而且影子的方向也在改变．根据不同时刻影长的变 换规律，以及太阳东____西______的自然规律，可以判断时间的先后顺序．‎ 平行投影与视图的联系：事实上，在特殊位置下(投影线与投影面垂直时)‎ 物体的平行投影就是物体的三种视图．物体的主视图是一束平行光线从正前方照射时形成的平行投影；左视图是一束平行光线从左前方照射形成的平行投影； 俯视图是一束平行光线从正上方照射形成的平行投影．‎ ‎【中心投影】由同一点（点光源发出的光线）形成的投影。探照灯、手电筒、路灯的光线可以看成是从一点出发的，像这样的光线所形成的投影称为中心投影。‎ ‎【平行投影与中心投影的区别与联系】‎ ‎※区分平行投影和中心投影：①观察光源；②观察影子。‎ 投影 区 别 联系 光线 物体与投影面平行时的投影 平行投影 平行的投射线 全等 都是物体在光线的照射下，在某个平面内形成的影子。(即都是投影)‎ 中心投影 从一点出发的投射线 放大(位似变换)‎ ‎（1）分别过每个物体的顶端及其影子的顶端作一条直线，若两直线______，则为平行投影；若两直线_______，则为中心投影，其交点就是光源的位置．‎ ‎（2）中心投影光源的确定：分别过每个物体的顶端及其影子的顶端作一条直线，这两条直线的___________即为光源的位置．‎ ‎【补充说明】‎ ‎※从正面、上面、侧面看到的图形就是常见的正投影，是当光线与投影垂 ‎ 直时的投影。‎ ‎①点在一个平面上的投影仍是一个点； v ‎②线段在一个面上的投影可分为三种情况：‎ 线段垂直于投影面时，投影为一点；‎ 线段平行于投影面时，投影长度等于线段的实际长度；‎ 线段倾斜于投影面时，投影长度小于线段的实际长度。‎ ‎③平面图形在某一平面上的投影可分为三种情况：‎ 平面图形和投影面平行的情况下，其投影为实际形状；‎ 平面图形和投影面垂直的情况下，其投影为一线段；‎ 平面图形和投影面倾斜的情况下，其投影小于实际的形状。‎ ‎【视图】将人的视线规定为平行投影线，然后正对着物体看过去，将所见物体的轮廓用正投影法绘制出来该图形称为视图。‎ ‎1、三种视图的内在联系 主视图反映物体的_________；俯视图反映物体的________；左 ‎ 视图反映物体的______．因此，在画三种视图时，主、俯视图反映 ‎______，主、左视图反映______，俯、左视图反映_______．（填“长”、‎ ‎“宽”、“高”）‎ ‎2、三种视图的位置关系 一般地，首先确定主视图的位置，画出主视图，然后在主视图的 ‎　下面画出俯视图，在主视图的右边画出左视图．‎ ‎3、三种视图的画法 ‎ 　首先观察物体，画出视图的外轮廓线，然后将视图补充完整，其中看得见部分的轮廓线通常画成______线，看不见部分的轮廓线通常画成_______线．‎ ‎[注意] 在画圆锥的俯视图时，要注意不要漏掉圆心处的实点．‎ ‎4. 投影规则：主俯长对正、主左高平齐、俯左宽相等 ‎ 即：　主视图和俯视图的长要相等　 主视图和左视图的高要相等 ‎ ‎ 左视图和俯视图的宽要相等。‎ 在许多情况下，只用一个投影不加任何注解，是不能完整清晰地表达和确定形体的形状和结构的。如图所示，三个形体在同一个方向的投影完全相同，但三个形体的空间结构却不相同。可见只用一个方向的投影来表达形体形状是不行的。一般必须将形体向几个方向投影，才能完整清晰地表达出形体的形状和结构。 ‎ ‎※视图中每一个闭合的线框都表示物体上一个表面(平面或曲面)，而相连的两个闭合线框一定不在一个平面上。‎ ‎※在一个外形线框内所包括的各个小线框，一定是平面体（或曲面体）上凸出或凹的各个小的平面体（或曲面体）。‎ ‎※在画视图时，看得见的部分的轮廓线通常画成实线，看不见的部分轮廓线通常画成虚线。‎ ‎【三视图中的方位与物体上的方位的对应关系】‎ ‎(1)主视图中的上、下、左、右对应物体的上、下、左、右；‎ ‎(2)俯视图中的上、下、左、右对应物体的后、前、左、右；‎ ‎(3)左视图中的上、下、左、右对应物体的上、下、后、前．‎ ※ 根据正视图和左视图确定小方块堆的俯视图的规律为：‎ 正视图与俯视图的列数相同，其每列的方块数是俯视 图中该列中的最大数字；左视图的列数与俯视图的行 数相同，其每列的方块数是俯视图中该行中的最大数字.‎ ‎【视点、视线、盲区】‎ 眼睛的位置称为视点；由视点发出的光线称为视线；眼睛看不到的地方称为盲区．‎