高考数学复习专题练习第2讲 相关性、最小二乘估计与统计案例

高考数学复习专题练习第2讲 相关性、最小二乘估计与统计案例

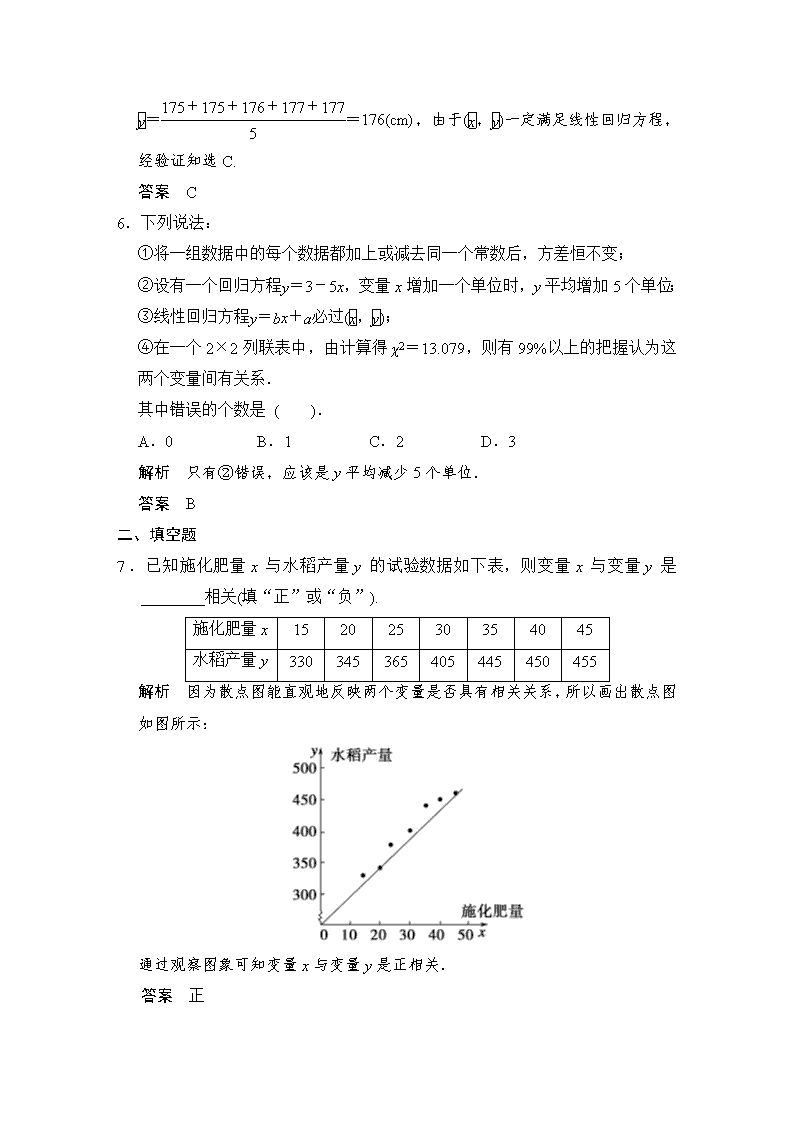
第2讲 相关性、最小二乘估计与统计案例 一、选择题 ‎1．在一组样本数据(x1，y1)，(x2，y2)，…，(xn，yn)(n≥2，x1，x2，…，xn不全相等)的散点图中，若所有样本点(xi，yi)(i＝1,2，…，n)都在直线y＝x＋1上，则这组样本数据的样本相关系数为(　　)．‎ A．－1 B．‎0 ‎ C. D．1‎ 答案　D ‎2．已知x，y取值如下表：‎ x ‎0‎ ‎1‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎1.3‎ ‎1.8‎ ‎5.6‎ ‎6.1‎ ‎7.4‎ ‎9.3‎ 从所得的散点图分析可知：y与x线性相关，且＝0.95x＋a，则a＝(　　)．‎ A．1.30 B．‎1.45 ‎ C．1.65 D．1.80‎ 解析　依题意得，＝×(0＋1＋4＋5＋6＋8)＝4，＝×(1.3＋1.8＋5.6＋6.1＋7.4＋9.3)＝5.25.又直线＝0.95x＋a必过样本中心点(，)，即点(4,5.25)，于是有5.25＝0.95×4＋a，由此解得a＝1.45，选B.‎ 答案　B ‎3. 设(x1，y1)，(x2，y2)，…，(xn，yn)是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图)，以下结论正确的是 (　　)．‎ A．直线l过点(，)‎ B．x和y的相关系数为直线l的斜率 C．x和y的相关系数在0到1之间 D．当n为偶数时，分布在l两侧的样本点的个数一定相同 解析　由样本的中心(，)落在回归直线上可知A正确；x和y的相关系数表示为x与y之间的线性相关程度，不表示直线l的斜率，故B错；x和y 的相关系数应在－1到1之间，故C错；分布在回归直线两侧的样本点的个数并不绝对平均，即无论样本点个数是奇数还是偶数，故D错．‎ 答案　A ‎4．某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程＝x＋中的为9.4，据此模型预报广告费用为6万元时销售额为 (　　)．‎ A．63.6万元 B．65.5万元 C．67.7万元 D．72.0万元 解析　＝＝3.5(万元)，‎ ＝＝42(万元)，‎ ‎∴＝－＝42－9.4×3.5＝9.1，‎ ‎∴回归方程为＝9.4x＋9.1，‎ ‎∴当x＝6(万元)时，＝9.4×6＋9.1＝65.5(万元)．‎ 答案　B ‎5．为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下：‎ 父亲身高x/cm ‎174‎ ‎176‎ ‎176‎ ‎176‎ ‎178‎ 儿子身高y/cm ‎175‎ ‎175‎ ‎176‎ ‎177‎ ‎177‎ 则y对x的线性回归方程为 (　　)．‎ A．y＝x－1 B．y＝x＋1‎ C．y＝88＋x D．y＝176‎ 解析　由题意得＝＝176(cm)，‎ ＝＝176(cm)，由于(，)一定满足线性回归方程，经验证知选C.‎ 答案　C ‎6．下列说法：‎ ‎①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；‎ ‎②设有一个回归方程＝3－5x，变量x增加一个单位时，y平均增加5个单位；‎ ‎③线性回归方程＝x＋必过(，)；‎ ‎④在一个2×2列联表中，由计算得χ2＝13.079，则有99%以上的把握认为这两个变量间有关系．‎ 其中错误的个数是 (　　)．‎ A．0 B．‎1 ‎ C．2 D．3‎ 解析　只有②错误，应该是y平均减少5个单位．‎ 答案　B 二、填空题 ‎7．已知施化肥量x与水稻产量y的试验数据如下表，则变量x与变量y是________相关(填“正”或“负”).‎ 施化肥量x ‎15‎ ‎20‎ ‎25‎ ‎30‎ ‎35‎ ‎40‎ ‎45‎ 水稻产量y ‎330‎ ‎345‎ ‎365‎ ‎405‎ ‎445‎ ‎450‎ ‎455‎ 解析　因为散点图能直观地反映两个变量是否具有相关关系，所以画出散点图如图所示：‎ 通过观察图象可知变量x与变量y是正相关．‎ ‎ 答案　正 ‎8．考古学家通过始祖鸟化石标本发现：其股骨长度x(cm)与肱骨长度y(cm)的线性回归方程为＝1.197x－3.660，由此估计，当股骨长度为‎50 cm时，肱骨长度的估计值为________ cm.‎ 解析　根据线性回归方程＝1.197x－3.660，将x＝50代入得y＝56.19，则肱骨长度的估计值为‎56.19 cm.‎ 答案　56.19‎ ‎9．为了判断高中三年级学生是否选修文科与性别的关系，现随机抽取50名学生，得到如下2×2列联表：‎ 理科 文科 男 ‎13‎ ‎10‎ 女 ‎7‎ ‎20‎ χ2＝≈4.844.‎ 则认为选修文科与性别有关系的可能性约为________．‎ 解析　∵χ2≈4.844，这表明小概率事件发生．根据假设检验的基本原理，应该断定“是否选修文科与性别之间有关系”成立，并且这种判断正确的可能性约为95%.‎ 答案　95%‎ ‎10．某数学老师身高‎176 cm，他爷爷、父亲和儿子的身高分别是‎173 cm、‎170 cm和‎182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________ cm.‎ 解析　由题意父亲身高x cm与儿子身高y cm对应关系如下表：‎ x ‎173‎ ‎170‎ ‎176‎ y ‎170‎ ‎176‎ ‎182‎ 则＝＝173，＝＝176，‎ (xi－)(yi－)＝(173－173)×(170－176)＋(170－173)×(176－176)＋(176－173)(182－176)＝18，‎ (xi－)2＝(173－173)2＋(170－173)2＋(176－173)2＝18.∴＝＝1.∴＝－ ＝176－173＝3.‎ ‎∴线性回归直线方程＝x＋＝x＋3.‎ ‎∴可估计孙子身高为182＋3＝185(cm)．‎ 答案　185‎ 三、解答题 ‎11．某班主任对全班50名学生进行了作业量多少的调查．数据如下表：‎ 认为作业多 认为作业不多 合计 喜欢玩游戏 ‎18‎ ‎9‎ 不喜欢玩游戏 ‎8‎ ‎15‎ 合计 ‎(1)请完善上表中所缺的有关数据；‎ ‎(2)试通过计算说明有多大把握认为喜欢玩游戏与作业量的多少有关系？‎ 解　(1)‎ 认为作业多 认为作业不多 合计 喜欢玩游戏 ‎18‎ ‎9‎ ‎27‎ 不喜欢玩游戏 ‎8‎ ‎15‎ ‎23‎ 合计 ‎26‎ ‎24‎ ‎50‎ ‎(2)将表中的数据代入公式χ2＝ ‎＝≈5.059>3.841，‎ 即说明有95%以上的把握认为喜欢玩游戏与作业量的多少有关系．‎ ‎12．下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎(1)请画出上表数据的散点图；‎ ‎(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程＝x＋；‎ ‎(3)已知该厂技改前生产100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？‎ ‎(参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5)‎ 解　(1)由题设所给数据，可得散点图如图所示．‎ ‎(2)由对照数据，计算得：＝86，‎ ＝＝4.5(吨)，＝＝3.5(吨)．‎ 已知iyi＝66.5，‎ 所以，由最小二乘法确定的回归方程的系数为：‎ ＝＝＝0.7，‎ ＝－＝3.5－0.7×4.5＝0.35.‎ 因此，所求的线性回归方程为y＝0.7x＋0.35.‎ ‎(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗，得降低的生产能耗为：‎ ‎90－(0.7×100＋0.35)＝19.65(吨标准煤)．‎ ‎13． 某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了‎12月1日至‎12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：‎ 日期 ‎12月1日 ‎12月2日 ‎12月3日 ‎12月4日 ‎12月5日 温差x/℃‎ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数y/颗 ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．‎ ‎(1)求选取的2组数据恰好是不相邻2天数据的概率；‎ ‎(2)若选取的是‎12月1日与‎12月5日的两组数据，请根据‎12月2日至‎12月4日的数据，求出y关于x的线性回归方程y＝bx＋a.‎ 解　(1)设抽到不相邻两组数据为事件A，因为从5组数据中选取2组数据共有10种情况，每种情况都是等可能出现的，其中抽到相邻两组数据的情况有4种，‎ 所以P(A)＝1－＝.‎ ‎(2)由数据，求得＝12，＝27.‎ ‎11×25＋13×30＋12×26＝977，112＋132＋122＝434，‎ 由公式，求得b＝，a＝－b ＝－3.‎ 所以y关于x的线性回归方程为y＝x－3.‎ ‎14．有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.‎ 优秀 非优秀 总计 甲班 ‎10‎ 乙班 ‎30‎ 合计105‎ 已知从全部105人中随机抽取1人为优秀的概率为.‎ ‎(1)请完成上面的列联表；‎ ‎(2)根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系”；‎ ‎(3)若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到6号或10号的概率．‎ 解　(1)‎ 优秀 非优秀 总计 甲班 ‎10‎ ‎45‎ ‎55‎ 乙班 ‎20‎ ‎30‎ ‎50‎ 合计 ‎30‎ ‎75‎ ‎105‎ ‎(2)根据列联表中的数据，得到 χ2＝≈6.109＞3.841，‎ 因此有95%的把握认为“成绩与班级有关系”．‎ ‎(3)设“抽到6号或10号”为事件A，先后两次抛掷一枚均匀的骰子，出现的点数为(x，y)，则所有的基本事件有(1,1)、(1,2)、(1,3)、…、(6,6)，共36个．‎ 事件A包含的基本事件有(1,5)，(2,4)，(3,3)，(4,2)，(5,1)，(4,6)，(5,5)，(6,4)，共8个，‎ ‎∴P(A)＝＝.‎