- 2021-05-10 发布 |
- 37.5 KB |
- 11页

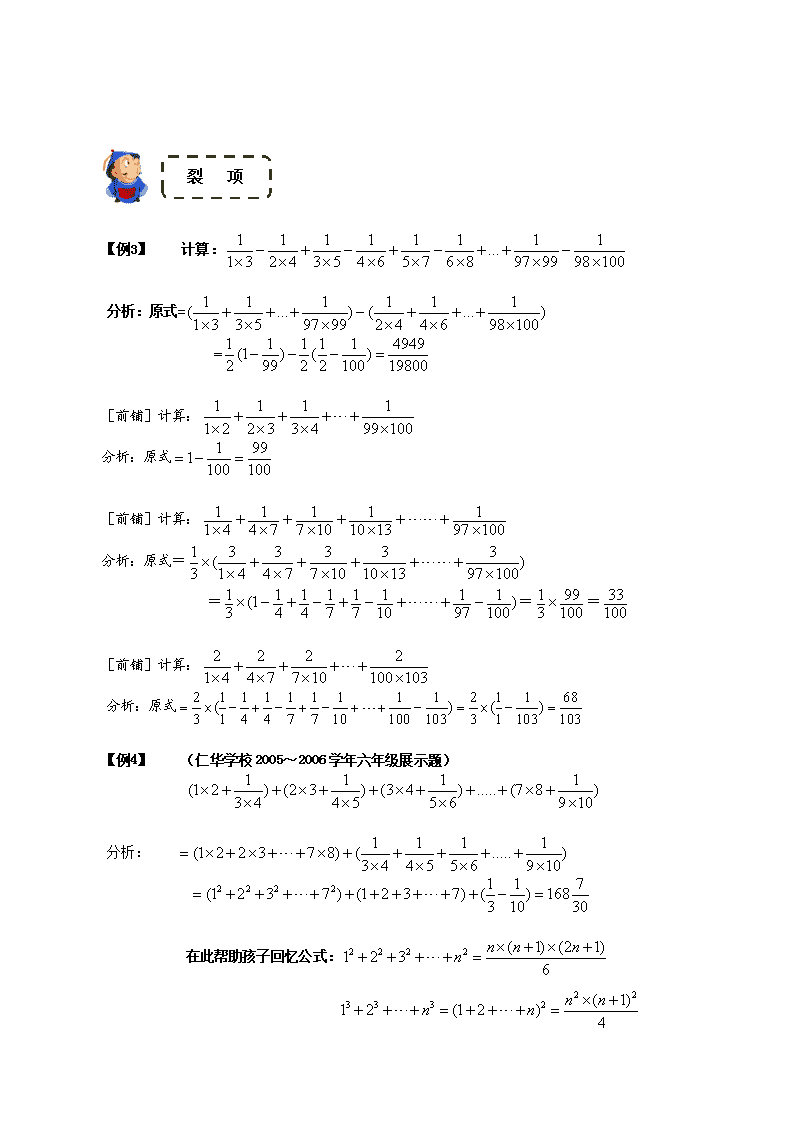
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学试题-奥数:计算之裂项、换元与通项归纳(解析版)全国通用
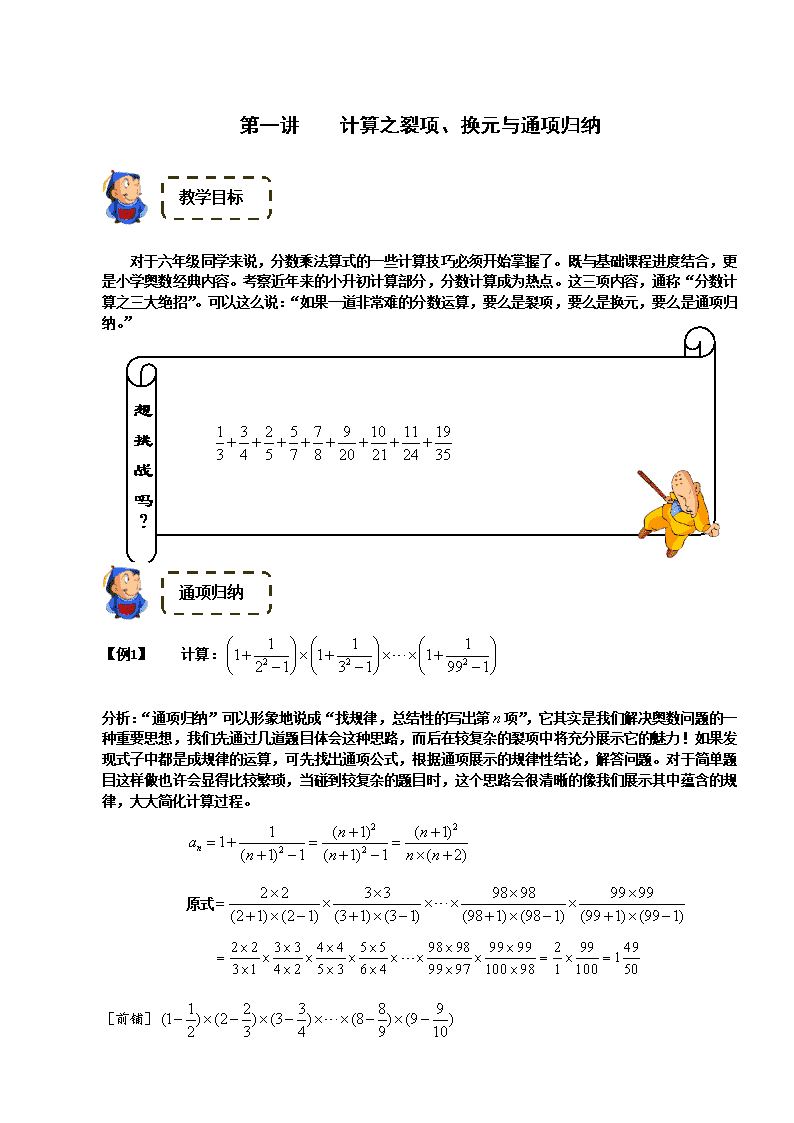
第一讲 计算之裂项、换元与通项归纳 教学目标 对于六年级同学来说,分数乘法算式的一些计算技巧必须开始掌握了。既与基础课程进度结合,更 是小学奥数经典内容。考察近年来的小升初计算部分,分数计算成为热点。这三项内容,通称“分数计 算之三大绝招”。可以这么说:“如果一道非常难的分数运算,要么是裂项,要么是换元,要么是通项归 纳。” 通项归纳 【例 1】 计算: 2 2 2 1 1 11 1 1 2 1 3 1 99 1 分析:“通项归纳”可以形象地说成“找规律,总结性的写出第 n 项”,它其实是我们解决奥数问题的一 种重要思想,我们先通过几道题目体会这种思路,而后在较复杂的裂项中将充分展示它的魅力!如果发 现式子中都是成规律的运算,可先找出通项公式,根据通项展示的规律性结论,解答问题。对于简单题 目这样做也许会显得比较繁琐,当碰到较复杂的题目时,这个思路会很清晰的像我们展示其中蕴含的规 律,大大简化计算过程。 2 2 2 2 1 ( 1) ( 1)1 ( 1) 1 ( 1) 1 ( 2)n n na n n n n 原式 2 2 3 3 98 98 99 99 (2 1) (2 1) (3 1) (3 1) (98 1) (98 1) (99 1) (99 1) 2 2 3 3 4 4 5 5 98 98 99 99 2 99 491 3 1 4 2 5 3 6 4 99 97 100 98 1 100 50 [前铺] 1 2 3 8 9(1 ) (2 ) (3 ) (8 ) (9 ) 2 3 4 9 10 想 挑 战 吗 ? 1 3 2 5 7 9 10 11 19 3 4 5 7 8 20 21 24 35 分析:通项为: 2( 1) 1 1 1n n n n n na n n n n , 原式 2 2 2 2 21 2 3 4 8 9 3 4 6 7 8 9 36288 2 3 4 5 9 10 [拓展]计算: 1 2 1 2 3 1 2 3 4 1 2 3 50 2 2 3 2 3 4 2 3 50 分析:找通项 (1 ) ( 1)2 (1 ) ( 1) 21 2 n n n n na n n n n 原式 2 3 3 4 4 5 5 6 2 3 3 4 4 5 5 6 4 10 18 28 1 4 2 5 3 6 4 7 , 通过试写我们又发现数列存在以上规律,这样我们就可以轻松写出全部的项,所以有 原式 2 3 3 4 4 5 5 6 48 49 49 50 50 51 1 4 2 5 3 6 4 7 47 50 48 51 49 52 3 50 232 1 52 26 【例 2】 计算: 2 2 2 2 2 2 2 21 2 2 3 2004 2005 2005 2006 1 2 2 3 2004 2005 2005 2006 分析:(法 1):可先来分析一下它的通项情况, 2 2 2 2( 1) ( 1) 1 ( 1) ( 1) ( 1) 1n n n n n n na n n n n n n n n 原式= 2 1 3 2 4 3 5 4 2005 2004 2006 2005( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 3 3 4 4 5 2004 2005 2005 2006 2005 20052005 2 4010 2006 2006 (法 2): 2 2 2 2 2 ( 1) 2 2 1 1 12 2 ( 1) ( 1)n n n n na n n n n n n n n ,也可用“裂项思路”解 答问题,进而可以过渡到下一个专题! [拓展]计算: 333 222 3333 2222 333 222 33 22 3 2 2621 2621 4321 4321 321 321 21 21 1 1 分析: 2 2 2 2 23 3 3 ( 1) (2 1) 1 2 2 2 1 2 1 16 ( ) ( 1)1 2 3 ( 1) 3 1 4 n n n n n na n nn n n n n 原式= 2 1 1 1 1 1 1 1 1[( ) ( ) ( ) ( )] 3 1 2 2 3 3 4 26 27 = 2 1 52(1 ) 3 27 81 裂 项 【例 3】 计算: 1 1 1 1 1 1 1 1... 1 3 2 4 3 5 4 6 5 7 6 8 97 99 98 100 分析:原式= 1 1 1 1 1 1( ... ) ( ... ) 1 3 3 5 97 99 2 4 4 6 98 100 = 1 1 1 1 1 4949(1 ) ( ) 2 99 2 2 100 19800 [前铺]计算: 1 1 1 1 1 2 2 3 3 4 99 100 分析:原式 1 991 100 100 [前铺]计算: 10097 1 1310 1 107 1 74 1 41 1 分析:原式= 1 3 3 3 3 3( ) 3 1 4 4 7 7 10 10 13 97 100 = ) 100 1 97 1 10 1 7 1 7 1 4 1 4 11( 3 1 = 100 99 3 1 = 100 33 [前铺]计算: 2 2 2 2 1 4 4 7 7 10 100 103 分析:原式 2 1 1 1 1 1 1 1 1 2 1 1 68( ) ( ) 3 1 4 4 7 7 10 100 103 3 1 103 103 【例 4】 (仁华学校 2005~2006 学年六年级展示题) 1 1 1 1(1 2 ) (2 3 ) (3 4 ) ..... (7 8 ) 3 4 4 5 5 6 9 10 分析: 1 1 1 1(1 2 2 3 7 8) ( ..... ) 3 4 4 5 5 6 9 10 2 2 2 2 1 1 7(1 2 3 7 ) (1 2 3 7) ( ) 168 3 10 30 在此帮助孩子回忆公式: 2 2 2 2 ( 1) (2 1)1 2 3 6 n n nn 2 2 3 3 3 2 ( 1)1 2 (1 2 ) 4 n nn n [前铺] 1 1 1 1 11 2 3 4 8 3 15 35 63 255 分析:原式 1 1 1 1(1 2 3 8) ( ) 1 3 3 5 5 7 15 17 1 1 1 1 1 1 836 (1 ) ( ) ( ) 36 2 3 3 5 15 17 17 【例 5】 计算: 1 5 1 19 1 41 1 71 11 2 3 4 5 6 7 8 9 2 6 12 20 30 42 56 72 90 分析:原式可变形为: 1 1 1 1 1 1 1 1 1(1 ) (3 ) (3 ) (5 ) (5 ) (7 ) (7 ) (9 ) (9 ) 2 6 12 20 30 42 56 72 90 1 1 1 1 1 1 1 1 1(1 3 3 5 5 7 7 9 9) ( ) 2 6 12 20 30 42 56 72 90 1 1 1 1 1 1 1 1 19 [( ) ( )] 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 4 1 839 ( ) 5 10 10 [前铺] 14 34 62 98 142 194 254 322 398 482 15 35 63 99 143 195 255 323 399 483 分析:原式 1 1 1 1 1 1(1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 15 35 63 99 399 483 1 1 1 1 1 1 5910 ( ) 10 ( ) 9 3 5 5 7 21 23 2 3 23 69 【例 6】 计算: 2 2 2 2 2 2 2 2 2 2 2 2 3 1 5 1 7 1 9 1 11 1 13 1 3 1 5 1 7 1 9 1 11 1 13 1 分析:原式= ) 1412 21() 1210 21() 108 21() 86 21() 64 21() 42 21( 1 1 1 36 2 ( ) 6 2 14 2 7 [前铺]计算: 113 1 111 1 19 1 17 1 15 1 13 1 222222 分析:原式 ) 1412 1() 1210 1() 108 1() 86 1() 64 1() 42 1( 1 1 1 1 1 1 1 1 1 1 1 1 1 3( ) 2 4 4 6 6 8 8 10 10 12 12 14 2 14 【例 7】 2 2 4 4 6 6 8 8 10 10 1 3 3 5 5 7 7 9 9 11 分析:(法 1):可先找通项, 2 2 2 1 11 1 1 1 ( 1) ( 1)n na n n n n 原式 1 1 1 1 1(1 ) (1 ) (1 ) (1 ) (1 ) 1 3 3 5 5 7 7 9 9 11 1 1 5 55 (1 ) 5 5 2 11 11 11 (法 2):原式 2 8 8 18 18 32 32 50 50(2 ) ( ) ( ) ( ) ( ) 3 3 5 5 7 7 9 9 11 6 10 14 18 50 6 52 10 4 5 3 5 7 9 11 11 11 【例 8】 计算: 1 1 11 1 2 1 2 3 1 2 2007 分析: 先找通项公式 1 2 1 12( ) 1 2 ( 1) 1na n n n n n 原式 1 1 11 2 (2 1) 3 (3 1) 2007 (2007 1) 2 2 2 2 2 2 2 1 2 2 3 3 4 2007 2008 20072 2008 2007 1004 【例 9】 计算: 1 11 3 19992 1 1 1 1 1 11 (1 ) (1 ) (1 ) (1 ) (1 ) 2 2 3 2 3 1999 分析: 1 1 2 1 11 1 2 ( )1 1 1 2 ( 1)( 2) 1 2(1 ) (1 ) (1 ) 2 3 1 2 n n n n n n n n 原式= 1 1 1 1 1 1 1 1( ) ( ) ( ) ( ) 2 2 3 3 4 4 5 1999 2000 = 1000 999 1000 11 【例 10】 计算: 1 2 3 9 1 2 1 2 3 1 2 3 4 1 2 3 10 分析: (法 1):原式 1 1 1 1 1 1( ) ( ) ( ) 1 1 2 1 2 1 2 3 1 2 3 9 1 2 3 10 9 36287991 1 2 3 10 3628800 (法 2):原式 1 9 1 1 1 2 1 2 3 9 10 1 2 3 10 1 2 3 10 9 36287991 1 2 3 10 3628800 [前铺]计算: 1 1 1 1 1 3 5 3 5 7 5 7 9 2001 2003 2005 分析:原式 1 1 1 1 1 1 1( ) ( ) ( ) 4 1 3 3 5 3 5 5 7 2001 2003 2003 2005 1 1 1 1004003( ) 4 3 2003 2005 12048045 [拓展]计算: 2 3 101 1 (1 2) (1 2) (1 2 3) (1 2 9) (1 2 10) 分析: 1 1 [1 2 ( 1)][1 2 ( 1) ] 1 2 ( 1) 1 2 ( 1)n na n n n n n n 原式 1 1 1 1 1 11 ( ) ( ) ( ) 1 1 2 1 2 1 2 3 1 2 9 1 2 9 10 1 1 1 2 10 55 【例 11】 1 7 9 11 13 15 17 191 3 12 20 30 42 56 72 90 分析:原式 1 1 1 1 1 1 1 1 1 9( ) ( ) ( ) ( ) 1 1 3 3 4 4 5 9 10 10 10 【例 12】 1 1 1 1 1 20 10 26 38 27 2 3 30 31 41 51 119 120 123 124 分析:原式= 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1( ) ( ) ( ) ( ) ( ) 2 2 3 30 31 41 3 17 7 17 4 30 3 41 4 31 7 对于部分的裂项,可能不容易看到。我们通过这道例题,体会一下,如果能裂项成与 已知分数相同的部分,最终将出现前后抵消的效果。 [巩固] 1 3 2 5 7 9 10 11 19 3 4 5 7 8 20 21 24 35 分析:此题是“想挑战吗?”部分的展示题目, 原式 1 3 2 5 7 1 1 1 1 1 1 2 1 1 1 1 1 1 5 3 4 5 7 8 4 5 3 7 3 8 5 7 [巩固]计算: 42 13 30 11 20 9 12 7 6 5 7 6 5 3 分析:原式= 3 6 1 1 1 1 1 1 1 1 1 1 4 5 7 2 3 3 4 4 5 5 6 6 7 本专题小结:将算式中的项进行拆分,使拆分后的项可前后抵消,这种拆项计算称为裂项法.一般裂项时 可以利用以下式子: ① 1 1 1 ( 1) 1n n n n ② 1 1 1 1( ) ( )n n k k n n k ③ 1 1 1 1[ ] ( 1)( 2) 2 ( 1) ( 1)( 2)n n n n n n n 换 元 【例 13】 计算: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1(1 ... ) ( ... ) ( ... ) (1 ... ) 2 3 4 99 100 2 3 4 99 2 3 4 99 100 2 3 4 99 分析:设 1 1 1 1 1... 2 3 4 99 100 a , 则原式可化为: 1 1 1(1 )( ) (1 ) 100 100 100 a a a a . [前铺]计算: (10 876 312) (876 312 918) (10 876 312 918) (876 31 2) 分析:设 876 312, 876 312 918x y 原式 (10 ) (10 ) ( ) 10 9180x y y x y x [前铺]计算: 1 1 1 1 1 1 1 1 1 1 1 1 1 1(1 ) ( ) (1 ) ( ) 2 3 4 2 3 4 5 2 3 4 5 2 3 4 分析:设 1 1 1 2 3 4 a ,则原式化简为: 1 1 11 (1 5 5 5 a a a a( + )( + )- + )= [前铺] 947 458 358 739 207 378 947 458 358 739 126 621 207 378 947 458 358 739 947 458 358 739 126 621 分析:设 621 739 458 739 458, 126 358 947 358 947 a b 原式 378 378 378 621 378( ) ( ) ( ) 9 207 207 207 126 207 a b a b a b [巩固]计算: 1 1 1 1 1 1 1 1 1 1 1 1 1(1 1 2 3 1996 2 3 4 1997 2 3 1997 2 3 1996 )( )( )( ) 分析:采用换元思想.设 1 1 1 2 3 2006 x , 则原式= 1 1 1(1 )( ) (1 ) 1997 1997 1997 x x x x . 【例 14】 计算: 21 2 3 9 1 2 3 9 1 1 2 3 9 2 3 9( ) ( ) (1 ) ( ) 2 3 4 10 2 3 4 10 2 2 3 4 10 3 4 10 分析:设 1 2 3 9 2 3 4 10 t ,则有 2 2 21 1 1 1 1(1 )( ) ( ) 2 2 2 2 2 2 tt t t t t t t t [拓展]计算: 1 1 1 12 11 13 21 14 3 14 12005 12006 2005 2006 分析:设 12 13 14 12005 2006 a ,则原式 1 1 1 1 1 1 111 1 1 a aa a a a a a 专题展望 熟练掌握本节内容,寒假班我们要着重分析方法综合、通项归纳、扩缩法、换元法、估算法、尝试法。 练习一 1. 计算: 1 2 2 2 2 10 9 9 8 5 4 4 3 (对应例题 3) 分析:原式= ) 4 1 3 1 5 1 4 1 9 1 8 1 10 1 9 1(2 1 = ) 10 1 3 1(2 1 = 7 15 2. 420 120 20 14 12 13 6 12 2 11 (对应例题 4) 分析:原式 1 1 1 1 1(1 2 3 20) ( ) 2 6 12 20 420 1 1 1 1 1210 1 2 2 3 3 4 4 5 20 21 1 20210 (1 ) 210 21 21 3. 计算: 1 5 11 19 89 109 2 6 12 20 90 110 (对应例题 5) 分析:原式 1 1 1 1 1 1(1 ) (1 ) (1 ) (1 ) (1 ) (1 ) 2 6 12 20 90 110 1 1 1 1 1 1 1 110 ( ) 10 (1 ) 9 2 6 12 20 90 110 11 11 4. 计算: 1 1 11 1 2 1 2 3 1 2 2008 (对应例题 8) 分析:先找通项公式 1 2 1 12( ) 1 2 ( 1) 1na n n n n n 原式 1 1 11 2 (2 1) 3 (3 1) 2008 (2008 1) 2 2 2 2 2 2 2 1 2 2 3 3 4 2008 2009 20082 2009 4016 2009 5. 计算: 1 1 1 1... 1 2 3 2 3 4 3 4 5 99 100 101 (对应例题 10) 分析: 1 1 1 1[ ] ( 1)( 2) 2 ( 1) ( 1)( 2)na n n n n n n n 原式 1 1 1 1 1 1 1 1 1[( ) ( ) ( ) ... ( )] 2 1 2 2 3 2 3 3 4 4 5 5 6 99 100 100 101 1 1 1 5049 2 1 2 100 101 20200 6. 1 7 9 11 13 15 17 191 3 12 20 30 42 56 72 90 (对应例题 11) 分析:原式 1 1 1 1 1 1 1 1 1 9( ) ( ) ( ) ( ) 1 1 3 3 4 4 5 9 10 10 10 7. 计算:(对应例题 13、14) 1 1 1 1 1 1 1 1 1 11 1 2 2007 2 3 2008 2 2008 2 3 2007 分析:令 1 1 2 2007 a , 1 1 1 2 3 2008 b 原式 1(1 ) (1 ) 2008 a b b a b ab a ab b a 一定要学生抓住本题的重点是看见题目中有相同的因式而且不好直接乘开,所以我们 才采用这种方法的。 成长故事 有一只小麻雀飞到森林里,看到了一只孔雀,他觉得孔雀的翅膀是如此美丽,再看看自己这么丑, 这么小的翅膀,自卑感油然而生。到了晚上,小麻雀做了一个梦,在梦里边成了一只美丽的孔雀,正兴 高采烈地展现自己的翅膀时,突然有一只狼迎面扑来,小麻雀努力地振翅想逃,发现自己已经不能飞翔 了,吓得它惊惶醒来。小麻雀心想还好只是个梦。有一天,小麻雀飞到一座高山上,他看到老鹰飞得好 高好高,又好威风,自己跟老鹰比起来真是太渺小了。一会儿小麻雀靠着树干睡着了,梦见自己变成了 老鹰,任意飞驰于天空好不神气,但是,他以前的好友却都离他而去,不敢再与他为伍了。他突然觉得 好孤单,还是当小麻雀的日子比较快乐,醒来后他好庆幸自己还是一只小麻雀。看重自己,你就会发现 其实自己并非一无是处,保有自己的特性,做个充满自信的人,你将会是个独一无二的你!查看更多