中考数学规律题压轴题

中考数学规律题压轴题

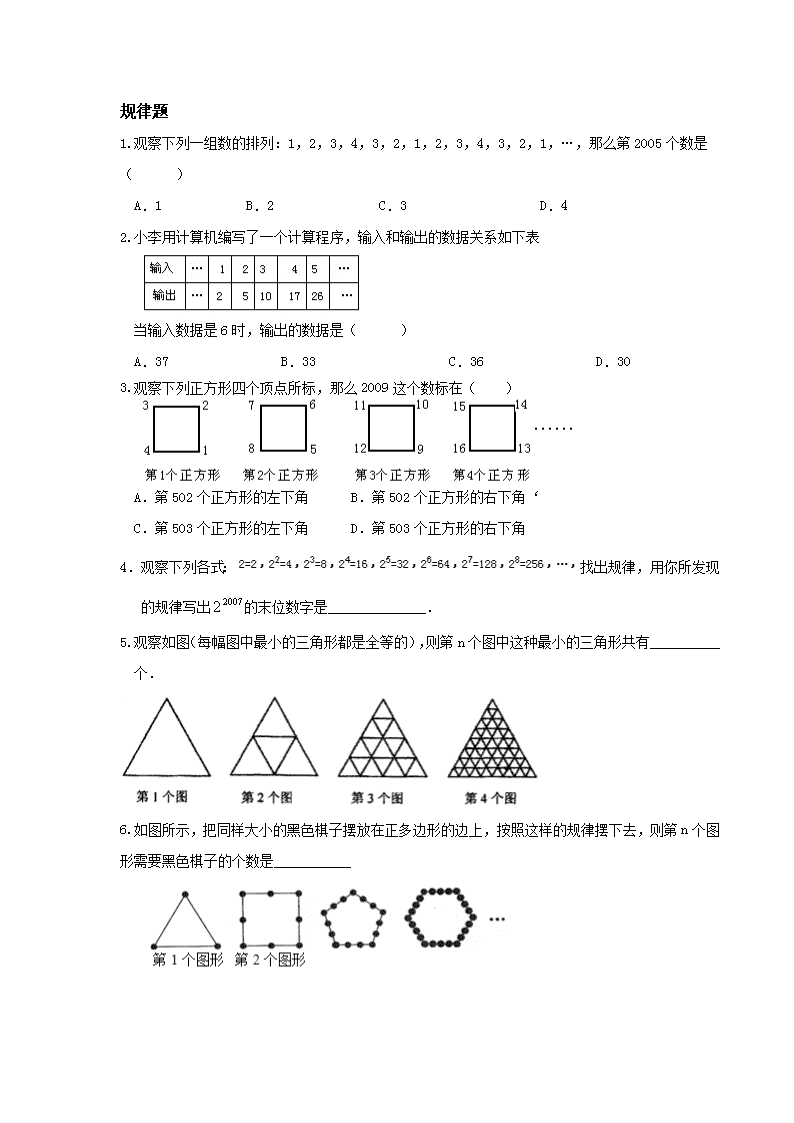
规律题 ‎1.观察下列一组数的排列：1，2，3，4，3，2，1，2，3，4，3，2，1，…，那么第2005个数是（　 　）‎ A．1 B．‎2 ‎‎ C．3 D．4‎ ‎2.小李用计算机编写了一个计算程序，输入和输出的数据关系如下表 当输入数据是6时，输出的数据是（　 　）‎ A．37 B．‎33 C．36 D．30‎ ‎3.观察下列正方形四个顶点所标，那么2009这个数标在（　　） ‎ A．第502个正方形的左下角 B．第502个正方形的右下角‘‎ C．第503个正方形的左下角 D．第503个正方形的右下角 ‎4．观察下列各式：找出规律，用你所发现的规律写出的末位数字是______________．‎ ‎5.观察如图（每幅图中最小的三角形都是全等的），则第n个图中这种最小的三角形共有__________个．4n-1‎ ‎6.如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是___________‎ ‎  ‎ ‎7.观察表，寻找规律，表二、表三、表四分别是从表一中截取的一部分，其中a，b，c的值分别为（　 　） ‎ A．20，29，30 B．18，30，‎26 C．18，20，26 D．18，30，28‎ ‎8.下面是一个按某种规律排列的数阵：根据规律，自然数2 000应该排在从上向下数的第m行，是该行中的从左向右数的第n个数，那么m+n的值是（　　）‎ A．110 B．‎109 ‎‎ C．108 D．107‎ 代数压轴 ‎1.先看数列：1，2，4，8，…，．从第二项起，每一项与它的前一项的比都等于2，象这样，一个数列：；从它的第二项起，每一项与它的前一项的比都等于一个常数q，那么这个数列就叫等比数列，q叫做等比数列的公比．‎ 根据你的阅读，回答下列问题：‎ ‎（1）请你写出一个等比数列，并说明公比是多少？‎ ‎（2）请你判断下列数列是否是等比数列，并说明理由；,……；‎ ‎（3）有一个等比数列；已知；请求出它的第5项．‎ ‎3.数学家高斯在上学时曾经研究过这样一个问题，1+2+3+…+10=？‎ 经过研究，这个问题的一般性结论是1+2+3+…+n=n（n+1），其中n为正整数，现在我们来研究一个类似的问题：1×2+2×3+…+n（n+1）=？‎ 观察下面三个特殊的等式：‎ ‎1×2=（1×2×3-0×1×2）‎ ‎2×3=（2×3×4-1×2×3）‎ ‎3×4=（3×4×5-2×3×4）‎ 将这三个等式的两边相加，可以得到1×2+2×3+3×4=×3×4×5=20．‎ 读完这段材料，请你计算：‎ ‎（1）1×2+2×3+…+100×101=__________________；（直接写出结果）‎ ‎（2）1×2+2×3+…+n（n+1）；（写出计算过程）‎ ‎（3）1×2×3+2×3×4+…+n（n+1）（n+2）= _______________________‎ ‎4.阅读下列材料并填空．‎ 例：解方程|x+2|+|x+3|=5‎ 解：①当x＜-3时，x+2＜0，x+3＜0，‎ 所以|x+2|=-x-2，|x+3|=-x-3‎ 所以原方程可化为 得 ‎②当-3≤x＜-2时，x+2＜0，x+3≥0，‎ 所以|x+2|=-x-2，|x+3|=x+3‎ 所以原方程可化为-x-2+x+3=5‎ 所以此时原方程无解 ‎③当x≥-2时，x+2≥0，x+3＞0，‎ ‎（2）用上面的解题方法解方程：|x+1|-|x-2|=x-6．‎ ‎5. 先阅读理解下列例题，再按例题解一元二次不等式：6‎ 解：把6分解因式，得6=（3x－2）(2x－1)‎ 又6，所以（3x－2）(2x－1)＞0‎ 由有理数的乘法法则“两数相乘，同号得正”有 ‎(1) 或（2）‎ 解不等式组（1）得x>； 解不等式组（2）得x〈‎ 所以（3x－2）(2x－1)＞0的解集为x>或x<‎ 利用以上方法求分式不等式<0的解集。‎ ‎6.比较正五边形与正六边形，可以发现它们的相同点和不同点．例如：‎ 它们的一个相同点：正五边形的各边相等，正六边形的各边也相等．‎ 它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形．‎ 请你再写出它们的两个相同点和不同点：‎ 相同点：① ___________________； 都②___________________；‎ 不同点：①；___________________；②___________________；‎ ‎7.阅读理解：‎ 在△ABC中，BC=a，CA=b，AB=c； （1）若∠C为直角，则a2+b2=c2；‎ ‎（2）若∠C为锐角，则a2+b2与c2的关系为：a2+b2＞c2‎ 证明：‎ ‎（3）若∠C为钝角，试推导a2+b2与c2的关系．‎ 探究问题：在△ABC中，BC=a=3，CA=b=4，AB=c；若△ABC是钝角三角形，求第三边c的取值范围．‎ ‎8.用长度一定的不锈钢材料设计成外观为矩形的框架（如图①②③中的一种）‎ 设竖档AB=x米，请根据以上图案回答下列问题：（题中的不锈钢材料总长度均指各图中所有黑线的长度和，所有横档和竖档分别与AD、AB平行）‎ ‎（1）在图①中，如果不锈钢材料总长度为‎12米，当x为多少时，矩形框架ABCD的面积为‎3平方米？‎ ‎（2）在图②中，如果不诱钢材料总长度为‎12米，当x为多少时，矩形架ABCD的面积S最大？最大面积是多少？‎ ‎（3）在图③中，如果不锈钢材料总长度为a米，共有n条竖档，那么当x为多少时，矩形框架ABCD的面积S最大？最大面积是多少？‎ ‎9.解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式M、N的大小，只要作出它们的差M-N，若M-N＞0，则M＞N；若M-N=0，则M=N；若M-N＜0，则M＜N．‎ 问题解决 如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．‎ 类别应用 ‎（1）已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和 元/千克（a、b是正数， 且a≠b），试比较小丽和小颖所购买商品的平均价格的高低．‎ ‎（2）试比较图2和图3中两个矩形周长M1、N1的大小（b＞c）．‎ ‎10.归纳猜想：同学们，让我们一起进行一次研究性学习：‎ ‎（1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？‎ ‎（2）如图2将半径为R的正方形沿直线l向右翻滚，当正方形翻滚一周时，其中心O经过的路程是多少？ ‎ ‎（3）猜想：把正多边形翻滚一周，其中心O所经过的路程是多少（R为正多边形的半径，可参看图2）？请说明理由．‎ ‎ （4）进一步猜想：任何多边形都有一个外接圆，若将任意圆内接多边形翻滚一周时，其外心所经过的路程是否是一个定值（R为多边形外接圆的半径）？为什么？请以任意三角形为例说明（如图）． 通过以上猜想你可得到什么样的结论？请写出来．‎ ‎11.如图1，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起．‎ ‎ （1）如图2，将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，设 旋转时FC交BA于点H（H点不与B点重合），FE交DA于点G（G点不与D点重合）．求证：BH•GD=BF2‎ ‎（2）如图3，△ECF的顶点F在△ABD的BD边上滑动（F点不与B、D点重合），且CF始终经过点A，过点A作AG∥CE，交FE于点G，连接DG．探究：FD+DG= ．请予证明．‎ ‎12.张经理到老王的果园里一次性采购一种水果，他俩商定：张经理的采购价y(元／吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A，但包含端点C)．‎ ‎(1)求y与x之间的函数关系式；‎ ‎(2)已知老王种植水果的成本是2 800元／吨，那么张经理的采购量为多少时，老王在这次买卖中所获的利润w最大?最大利润是多少?‎ ‎【答案】解：(1) 由图像知 ‎ ‎(2)∵利润=收入-成本=采购价×采购量-成本，即 ‎ ‎ ‎∴由(1) 有 ‎ 是一次函数一段，最大值5200×20=104000‎ 是二次函数一段，当时，有 最大值。‎ ‎ 因此张经理的采购量为23吨时，老王在这次买卖中所获的利润w最大，最大利润是105800元。‎ ‎【考点】一次函数,二次函数。‎ ‎【分析】(1) 由图像知时,函数值为8000得;‎ ‎,由待定系数法可求得.‎ ‎(2)由利润、收入、成本的关系可推得的关系式,分析一次函数和二次函数的最大值可解.‎ ‎13.如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°．正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．‎ ‎ (1)请在所给的图中，用尺规画出点A在正方形整个翻滚过程中所经过的路线图；‎ ‎ (2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S．‎ ‎【答案】(1)①以D为圆心，AD=1为半径画弧，交MN于； ②以DN的中点E（ED=1）为圆心， EA=为半径画弧，和相交于；③以N为圆心，NE =1为半径画弧 ‎，和相交于，与NP相交于；④以P为圆心， =1为半径画弧；⑤在PQ上取F使PF=AD=1，以F为圆心， 为半径画弧，和相交于；⑥在PQ上取G使FG=AD=1，以G为圆心， 1为半径画弧，和相交于，交PQ于。‎ 则点A在正方形整个翻滚过程中所经过的路线图为弧。（画图过程略） ‎ ‎(2) 弧AA1与AD，A1D围成图形的面积；‎ 弧A‎1A2与A1D，DN，A2N围成图形的面积为：‎ 弧A‎2A3与A2N，NA3围成图形的面积为：‎ ‎ 其他三块小面积分别与以上三块相同.所以点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S为 ‎2.十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案（简称“个税法草案”），拟将现行个人所得税的起征点由每月2000元提高到3000元，并将9级超额累进税率修改为7级，两种征税方法的1～5级税率情况见下表：‎ 注：“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额．‎ ‎“速算扣除数”是为快捷简便计算个人所得税而设定的一个数．‎ 例如：按现行个人所得税法的规定，某人今年3月的应纳税额为2600元，他应缴税款可以用下面两种方法之一来计算：‎ 方法一：按1～3级超额累进税率计算，即500×5%+1500×10%+600×15%=265（元）．‎ 方法二：用“月应纳税额x适用税率-速算扣除数”计算，即2600×15%-125=265（元）．‎ ‎（1）请把表中空缺的“速算扣除数”填写完整；‎ ‎（2）甲今年3月缴了个人所得税1060元，若按“个税法草案”计算，则他应缴税款多少元？‎ ‎（3）乙今年3月缴了个人所得税3千多元，若按“个税法草案”计算，他应缴的税款恰好不变，那么乙今年3月所缴税款的具体数额为多少元？‎ ‎ ‎ 因为1060元在第3税级, 所以有20%x-525=1060, x=7925(元) 答: 他应缴税款7925元.‎ ‎ (3)缴个人所得税3千多元的应缴税款适用第4级, 假设个人收入为k, 刚有 ‎ 20%(k-2000) -375=25%(k-3000)-975 k=19000‎ ‎ 所以乙今年3月所缴税款的具体数额为(19000-2000)×20%-375=3025(元)‎ ‎【考点】统计图表的分析。‎ ‎【分析】(1) 当1500

查看更多