- 2021-05-10 发布 |
- 37.5 KB |
- 26页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021年九年级中考数学一轮复习精练+热考题型:几何变换综合题(四)
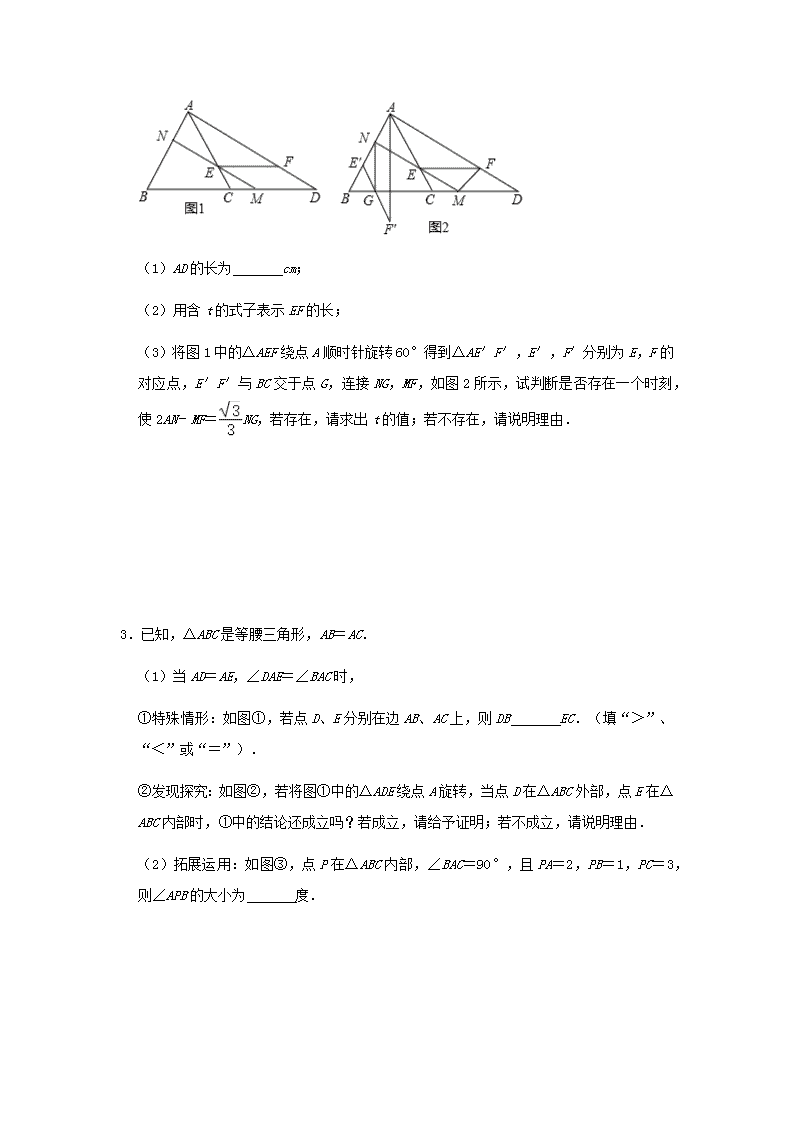
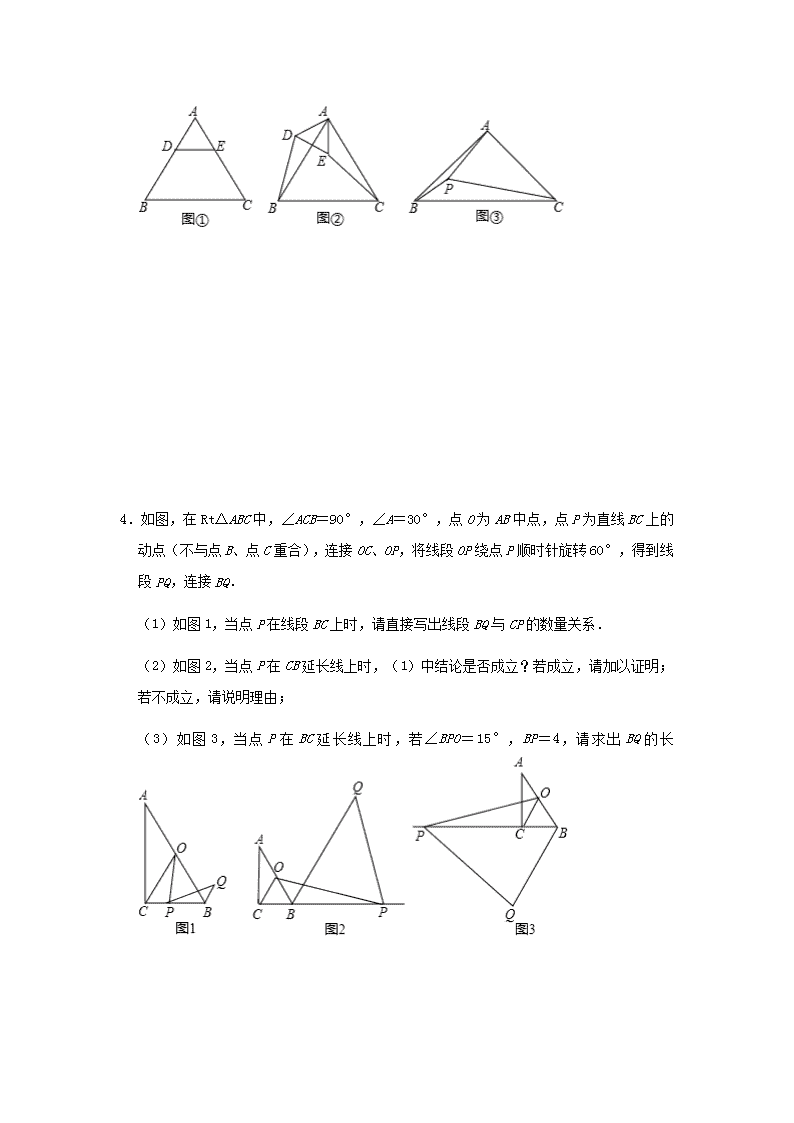
2021 年中考数学一轮复习精练+热考题型: 几何变换综合题(四) 1.在△ABC 中,以 AB 为斜边,作 Rt△ABD,使点 D 落在△ABC 内,∠ADB=90° (1)如图 1,若 AB=AC,∠BAD=30°,AD=2 ,点 P、M 分别为 BC、AB 边的中 点,连接 PM,求线段 PM 的长; (2)如图 2,若 AB=AC,把△ABD 绕点 A 逆时针旋转一定角度,得到△ACE,连接 ED 并延长交 BC 于点 P,求证:BP=CP (3)如图 3,若 AD=BD,过点 D 的直线交 AC 于点 E,交 BC 于点 F,EF⊥AC,且 AE=EC,请直接写出线段 BF、FC、AD 之间的关系(不需要证明). 2.如图 1,△ABC 是等边三角形,AB=6cm,过点 A 作 AB 的垂线,交 BC 的延长线于点 D, 点 M 从点 C 出发,沿 CD 以 2cm/s 的速度运动至点 D,同时点 N 从点 A 出发,沿 AB 以 2cm/s 的速度运动至点 B,连接 MN,交 AC 于点 E,过点 E 作 BC 的平行线,交 AD 于 点 F.设点 M 的运动时间为 t(s). (1)AD 的长为 cm; (2)用含 t 的式子表示 EF 的长; (3)将图 1 中的△AEF 绕点 A 顺时针旋转 60°得到△AE′F′,E′,F′分别为 E,F 的对应点,E′F′与 BC 交于点 G,连接 NG,MF,如图 2 所示,试判断是否存在一个 时刻,使 2AN﹣MF= NG,若存在,请求出 t 的值;若不存在,请说明理由. 3.已知,△ABC 是等腰三角形,AB=AC. (1)当 AD=AE,∠DAE=∠BAC 时, ①特殊情形:如图①,若点 D、E 分别在边 AB、AC 上,则 DB EC.(填“>”、 “<”或“=”). ②发现探究:如图②,若将图①中的△ADE 绕点 A 旋转,当点 D 在△ABC 外部,点 E 在△ABC 内部时,①中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由. (2)拓展运用:如图③,点 P 在△ABC 内部,∠BAC=90°,且 PA=2,PB=1,PC= 3,则∠APB 的大小为 度. 4.如图,在 Rt△ABC 中,∠ACB=90°,∠A=30°,点 O 为 AB 中点,点 P 为直线 BC 上的动点(不与点 B、点 C 重合),连接 OC、OP,将线段 OP 绕点 P 顺时针旋转 60°, 得到线段 PQ,连接 BQ. (1)如图 1,当点 P 在线段 BC 上时,请直接写出线段 BQ 与 CP 的数量关系. (2)如图 2,当点 P 在 CB 延长线上时,(1)中结论是否成立?若成立,请加以证明; 若不成立,请说明理由; (3)如图 3,当点 P 在 BC 延长线上时,若∠BPO=15°,BP=4,请求出 BQ 的长 5.已知:△ABC 和△ADE 均为等边三角形,连接 BE,CD,点 F,G,H 分别为 DE,BE, CD 中点. (1)当△ADE 绕点 A 旋转时,如图 1,则△FGH 的形状为 ,说明理由; (2)在△ADE 旋转的过程中,当 B,D,E 三点共线时,如图 2,若 AB=3,AD=2, 求线段 FH 的长; (3)在△ADE 旋转的过程中,若 AB=a,AD=b(a>b>0),则△FGH 的周长是否存 在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由. 6.已知四边形 ABCD 中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°, ∠MBN 绕 B 点旋转,它的两边分别交 AD,DC(或它们的延长线)于 E,F. (1)当∠MBN 绕 B 点旋转到 AE=CF 时(如图 1),若 AE=1,试求 AB 的长; (2)当∠MBN 绕 B 点旋转到 AE≠CF 时,在图 2 这种情况下,求证 AE+CF=EF; (3)当∠MBN 绕 B 点旋转到 AE≠CF 时,在图 3 这种情况下,(2)中结论是否成立? 若成立,请给予证明;若不成立,线段 AE、CF、EF 又有怎样的数量关系?请直接写出 你的猜想. 7.如图 1,线段 AB=m,以 AB 的中点 O 为顶角顶点,BO 为腰,2α(0°<α<90°)为 顶角,在 OB 上方作等腰三角形 OBC,连接 AC. (1)求证:AC⊥BC; (2)如图 2,将△OBC 绕顶点 O,逆时针旋转至△OB′C′,连结 BC′,AB′相交于 点 M. ①若 sinα= ,试求 的值; ②若 sinα= ,试探索:当△OBC 从 OB′与 OB 重合起,到 OC′与 OA 重合止的旋转 过程中,点 M 所经过的路径长. 8.如图 1,在 Rt△ABC 中,∠A=90°,AB=AC,点 D,E 分别在边 AB,AC 上,AD= AE,连接 DC,点 M,P,N 分别为 DE,DC,BC 的中点. (1)观察猜想:图 1 中,线段 PM 与 PN 的数量关系是 ,位置关系是 ; (2)探究证明:把△ADE 绕点 A 逆时针方向旋转到图 2 的位置,连接 MN,BD,CE, 判断△PMN 的形状,并说明理由; (3)拓展延伸:把△ADE 绕点 A 在平面内自由旋转,若 AD=4,AB=10,请直接写出 △PMN 面积的最大值. 9.如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,过点 B 做射线 BB1∥AC,动点 D 从点 A 出发沿射线 AC 方向以每秒 5 个单位的速度运动,同时动点 E 从点 C 出发沿射 线 AC 方向以每秒 3 个单位的速度运动,过点 D 作 DH⊥AB 于 H,过点 E 作 EF⊥AC 交 射线 BB1 于 F,连接 DF,设运动的时间为 t 秒(t>0). (1)当 t 为 时,AD=AB,此时 DE 的长度为 ; (2)当△DEF 与△ACB 全等时,求 t 的值; (3)以 DH 所在直线为对称轴,线段 AC 经轴对称变换后的图形为 A′C′. ①当 t> 时,设△ADA′的面积为 S,直接写出 S 关于 t 的函数关系式; ③当线段 A′C′与射线 BB1 有公共点时,求 t 的取值范围. 10.已知 O 为直线 MN 上一点,OP⊥MN,在等腰 Rt△ABO 中,∠BAO=90°,AC∥OP 交 OM 于 C,D 为 OB 的中点,DE⊥DC 交 MN 于 E. (1)如图 1,若点 B 在 OP 上,则 ①AC OE(填“<”,“=”或“>”); ②线段 CA、CO、CD 满足的等量关系式是 ; (2)将图 1 中的等腰 Rt△ABO 绕 O 点顺时针旋转α(0°<α<45°),如图 2,那么(1) 中的结论②是否成立?请说明理由; (3)将图 1 中的等腰 Rt△ABO 绕 O 点顺时针旋转α(45°<α<90°),请你在图 3 中 画出图形,并直接写出线段 CA、CO、CD 满足的等量关系式 . 参考答案 1.(1)解:∵∠ADB=90°,∠BAD=30°,AD=2 , ∴cos∠BAD= , ∴AB= = =4, ∴AC=AB=4, ∵点 P、M 分别为 BC、AB 边的中点, ∴PM= AC=2, (2)如图 2, 在 ED 上截取 EQ=PD, ∵∠ADB=90°, ∴∠BDP+∠ADE=90°, ∵AD=AE, ∴∠ADE=∠AED, ∵把△ABD 绕点 A 逆时针旋转一定角度,得到△ACE, ∴∠AEC=∠ADB=90° ∵∠AED+∠PEC=90°, ∴∠BDP=∠PEC, 在△BDP 和△CEQ 中, , ∴△BDP≌△CEQ, ∴BP=CQ,∠DBP=∠QCE, ∵∠CPE=∠BDP+∠DBP,∠PQC=∠PEC+∠QCE, ∴∠EPC=∠PQC, ∴PC=CQ, ∴BP=CP (3)BF2+FC2=2AD2, 理由:如图 3,连接 AF、CD. ∵EF⊥AC,且 AE=EC, ∴FA=FC,∠FAC=∠FCA, ∵EF⊥AC,且 AE=EC, ∴∠DAC=∠DCA,DA=DC, ∵AD=BD, ∴BD=DC, ∴∠DBC=∠DCB, ∵∠FAC=∠FCA,∠DAC=∠DCA, ∴∠DAF=∠DCB, ∴∠DAF=∠DBC, ∴∠AFB=∠ADB=90°, 在 Rt△ADB 中,DA=DB, ∴AB2=2AD2, 在 Rt△ABF 中,BF2+FA2=AB2=2AD2, ∵FA=FC ∴BF2+FC2=2AD2. 2.解:(1)如图 1 中, ∵△ABC 是等边三角形, ∴∠BAC=∠ACB=∠B=60°,AB=BC=AC=6, ∵DA⊥BA, ∴∠BAD=90°, ∴∠D=30°, ∴tan30°= , ∴ = , ∴AD=6 (cm), 故答案为 6 . (2)过点 N 作 NP∥AC,交 BC 于点 P. ∵PN∥AC ∴ = ,∵AB=CB, ∴AN=PC=2t, ∵CE∥PN, ∴ = , ∴ = , ∴EC=3﹣t, ∴AE=6﹣(3﹣t)=t+3, ∵EF∥CD, ∴∠AFE=∠D=30°, ∵∠CAD=90°﹣60°=30°, ∴∠EAF=∠EFA=30°, ∴EF=AE=t+3; (3)存在. 由题意易知 AE=AE′=t+3,∠AE′F′=∠AEF=120°, ∴∠BE′G=60°=∠B, ∴△BGE′是等边三角形, ∴BE′=GE′=BG=6﹣(t+3)=3﹣t,E′N=t+3﹣2t=3﹣t, ∴E′N=E′G,易知 NG= (3﹣t), ∵AE=EF=t+3,∠AEF=120°, ∴AF= (t+3), ∴DF=6 ﹣ (t+3)= (3﹣t), ∵DM=6﹣2t, ∴ = , = , ∴ = , ∴FM∥AB, ∴ = = , ∴FM=3﹣t, ∴4t﹣(3﹣t)= • (3﹣t), 解得 t=1 ∴当 t=1 时,2AN﹣MF= NG. 3.解:(1)①∵DE∥BC, ∴ = , ∵AB=AC, ∴DB=EC, 故答案为:=, ②成立. 证明:由①易知 AD=AE, ∴由旋转性质可知∠DAB=∠EAC, 在△DAB 和△EAC 中 , ∴△DAB≌△EAC, ∴DB=CE, (2)如图, 将△CPB 绕点 C 旋转 90°得△CEA,连接 PE, ∴△CPB≌△CEA, ∴CE=CP=2,AE=BP=1,∠PCE=90°, ∴∠CEP=∠CPE=45°, 在 Rt△PCE 中,由勾股定理可得,PE=2 , 在△PEA 中,PE2=(2 )2=8,AE2=12=1,PA2=32=9, ∵PE2+AE2=AP2, ∴△PEA 是直角三角形 ∴∠PEA=90°, ∴∠CEA=135°, 又∵△CPB≌△CEA ∴∠BPC=∠CEA=135°. 故答案为 135°. 4.解:(1)结论:BQ=CP. 理由:如图 1 中,作 PH∥AB 交 CO 于 H. 在 Rt△ABC 中,∵∠ACB=90°,∠A=30°,点 O 为 AB 中点, ∴CO=AO=BO,∠CBO=60°, ∴△CBO 是等边三角形, ∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°, ∴∠CHP=∠CPH=60°, ∴△CPH 是等边三角形, ∴PC=PH=CH, ∴OH=PB, ∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP, ∵∠OPQ=∠OCP=60°, ∴∠POH=∠QPB,∵PO=PQ, ∴△POH≌△QPB, ∴PH=QB, ∴PC=BQ. (2)成立:PC=BQ. 理由:作 PH∥AB 交 CO 的延长线于 H. 在 Rt△ABC 中,∵∠ACB=90°,∠A=30°,点 O 为 AB 中点, ∴CO=AO=BO,∠CBO=60°, ∴△CBO 是等边三角形, ∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°, ∴∠CHP=∠CPH=60°, ∴△CPH 是等边三角形, ∴PC=PH=CH, ∴OH=PB, ∵∠POH=60°+∠CPO,∠QPO=60°+∠CPO, ∴∠POH=∠QPB,∵PO=PQ, ∴△POH≌△QPB, ∴PH=QB, ∴PC=BQ. (3)如图 3 中,作 CE⊥OP 于 E,在 PE 上取一点 F,使得 FP=FC,连接 CF. ∵∠OPC=15°,∠OCB=∠OCP+∠POC, ∴∠POC=45°, ∴CE=EO,设 CE=EO=a,则 FC=FP=2a,EF= a, 在 Rt△PCE 中,PC= = =( + )a, ∵PC+CB=4, ∴( + )a+ a=4, 解得 a=4 ﹣2 , ∴PC=4 ﹣4, 由(2)可知 BQ=PC, ∴BQ=4 ﹣4. 5.解:(1)结论:△FGH 是等边三角形.理由如下: 如图 1 中,连接 BD、CE,延长 BD 交 CE 于 M,设 BM 交 FH 于点 O. ∵△ABC 和△ADE 均为等边三角形, ∴AB=AC,AD=AE,∠BAC=∠DAE, ∴∠BAD=∠CAE , ∴△BAD≌△CAE, ∴BD=CE,∠ADB=∠AEC, ∵EG=GB,EF=FD, ∴FG= BD,GF∥BD, ∵DF=EF,DH=HC, ∴FH= EC,FH∥EC, ∴FG=FH, ∵∠ADB+∠ADM=180°,∴∠AEC+∠ADM=180°, ∴∠DMC+∠DAE=180°, ∴∠DME=120°, ∴∠BMC=60° ∴∠GFH=∠BOH=∠BMC=60°, ∴△GHF 是等边三角形, 故答案为等边三角形. (2)如图 2 中,连接 AF、EC. 易知 AF⊥DE,在 Rt△AEF 中,AE=2,EF=DF=1, ∴AF= = , 在 Rt△ABF 中,BF= = , ∴BD=CE=BF﹣DF= ﹣1, ∴FH= EC= . (3)存在.理由如下. 由(1)可知,△GFH 是等边三角形,GF= BD, ∴△GFH 的周长=3GF= BD, 在△ABD 中,AB=a,AD=b, ∴BD 的最小值为 a﹣b,最大值为 a+b, ∴△FGH 的周长最大值为 (a+b),最小值为 (a﹣b). 6.证明:(1)如图 1 中, ∵Rt△ABE 和 Rt△CBF 中,AB=BC,CF=AE, ∴tan∠CBF=tan∠ABE,BF=BE, ∴∠CBF=∠ABE, ∵∠ABC=120°,∠MBN=60°, ∴∠CBF=30°,△BEF 是等边三角形, ∵AE=CF=1, ∴AB= AE= (2)如图 2,将 Rt△ABE 顺时针旋转 120°, ∵AB=BC,∠ABC=120°, ∴A 点与 C 点重合, ∴BG=BE,FG=CG+CF=AE+CF, ∵∠ABC=120°,∠MBN=60°,∠ABE=∠CBG, ∴∠GBF=60°, 在△GBF 和△EBF 中, , ∴△GBF≌△EBF(SAS), ∴FG=EF, ∴EF=AE+CF; (3)不成立,新结论为 EF=AE﹣CF. 理由:如图 3,将 Rt△ABE 顺时针旋转 120°, ∵AB=BC,∠ABC=120°, ∴A 点与 C 点重合,∠ABE=∠CBG, ∴BG=BE,FG=CG﹣CF=AE﹣CF, ∵∠ABC=∠ABE+∠CBE=120°, ∴∠CBG+∠CBE=∠GBE=120°, ∵∠MBN=60°, ∴∠GBF=60°, 在△BFG 和△BFE 中, , ∴△BFG≌△BFE,(SAS) ∴GF=EF, ∴EF=AE﹣CF. 7.(1)证明:如图 1 中, ∵OA=OB,OB=OC, ∴OA=OB=OC, ∴点 A、C、B 在以 AB 为直径的圆上, ∵AB 是⊙O 的直径, ∴∠ACB=90°, ∴AC⊥BC. (2)解:如图 2 中, ∵OA=OC′=OB′=OB, ∴A、B、C′、B′四点共圆, ∴∠A=∠BC′B′, ∵∠AMB=∠B′MC′, ∴△AMB∽△C′MB′, ∴ =( )2, ∵∠AB′B=90°,∠B′BC= ∠B′OC′=α, ∴sinα= = , ∴ =( )2= . (3)如图 3 中, 由(2)可知,当 sinα= 时,∠α=∠B′BM=30°, ∴∠B′MB=60°, ∴∠AMB=120°, 如图作等腰三角形△ABP,使得∠APB=120°, 以点 P 为圆心,PA 为半径作⊙P, ∵∠AMB 为优弧 AB 所对的圆周角, 当△OBC 从 OB′与 OB 重合起,到 OC′与 OA 重合止的旋转过程中,M 所经过的路径 为 , ∵AB=m,∴OA= m, ∴AP= m, ∴点 M 所经过的路径长为 = πm. 8.解:(1)∵点 P,N 是 BC,CD 的中点, ∴PN∥BD,PN= BD, ∵点 P,M 是 CD,DE 的中点, ∴PM∥CE,PM= CE, ∵AB=AC,AD=AE, ∴BD=CE, ∴PM=PN, ∵PN∥BD, ∴∠DPN=∠ADC, ∵PM∥CE, ∴∠DPM=∠DCA, ∵∠BAC=90°, ∴∠ADC+∠ACD=90°, ∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°, ∴PM⊥PN, 故答案为:PM=PN,PM⊥PN, (2)由旋转知,∠BAD=∠CAE, ∵AB=AC,AD=AE, ∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD=CE, 同(1)的方法,利用三角形的中位线得,PN= BD,PM= CE, ∴PM=PN, ∴△PMN 是等腰三角形, 同(1)的方法得,PM∥CE, ∴∠DPM=∠DCE, 同(1)的方法得,PN∥BD, ∴∠PNC=∠DBC, ∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, ∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC =∠BCE+∠DBC=∠ACB+∠ACE+∠DBC =∠ACB+∠ABD+∠DBC=∠ACB+∠ABC, ∵∠BAC=90°, ∴∠ACB+∠ABC=90°, ∴∠MPN=90°, ∴△PMN 是等腰直角三角形, (3)方法 1、如图 2,同(2)的方法得,△PMN 是等腰直角三角形, ∴MN 最大时,△PMN 的面积最大, ∴DE∥BC 且 DE 在顶点 A 上面, ∴MN 最大=AM+AN, 连接 AM,AN, 在△ADE 中,AD=AE=4,∠DAE=90°, ∴AM=2 , 在 Rt△ABC 中,AB=AC=10,AN=5 , ∴MN 最大=2 +5 =7 , ∴S△PMN 最大= PM2= × MN2= ×(7 )2= . 方法 2、由(2)知,△PMN 是等腰直角三角形,PM=PN= BD, ∴PM 最大时,△PMN 面积最大, ∴点 D 在 BA 的延长线上, ∴BD=AB+AD=14, ∴PM=7, ∴S△PMN 最大= PM2= ×72= 9.解:(1)在 Rt△ABC 中,AC=6,BC=8,根据勾股定理得,AB= =10, 由运动知,AD=5t, ∵AD=AB, ∴5t=10, ∴t=2, ∴CD=AD﹣AC=10﹣6=4,CE=3t=6, ∴DE=CE﹣CD=2, 故答案为 2,2; (2)∵∠ACB=90°,BB1∥AC,EF⊥AC, ∴四边形 BCEF 是矩形,EF=BC=8, 当 AD<AE 时,5t<6+3t, ∴0<t<3, 若 DE=AC,△ACB≌△DEF,DE=AE﹣AD=6+3t﹣5t=6﹣2t, ∴6﹣2t=6, ∴t=0, ∵t>0(不合题意,舍), 当 AD>AE 时,5t>6+3t, ∴t>3, 若 DE=AC,△ACB≌△DEF,DE=AD﹣AE=5t﹣6﹣3t=2t﹣6, ∴2t﹣6=6, ∴t=6, ∴当 t=6 时,△DEF 与△ACB 全等. (3)①如图, ∵∠ACB=∠AHD,∠BAC=∠DAH, ∴△ABC∽△ADH, ∴ , ∴ , ∴AH=3t,DH=4t, ∴S△ADA'=2S△ADH=2× AH×DH=AH×DH=12t2, ②当点 A'落在射线 BB1 上的点 B 时,AA'=AB=10, ∵DH⊥AB, ∴AA'=2AH=2×5t×cos∠A=6t=10, ∴t= , 当点 C'落在射线 BB1 上时,CC'∥AB, ∵BB1∥AC, ∴四边形 ACC'B 为平行四边形, ∴CC'=AB=10, ∵CC'=2CD×cos∠A=2×(5t﹣6)× = (5t﹣6), ∴t= , ∴ ≤t≤ ,线段 A'C'与射线 BB1 有公共点. 10.解:(1)①AC=OE, 理由:如图 1,∵在等腰 Rt△ABO 中,∠BAO=90°, ∴∠ABO=∠AOB=45°, ∵OP⊥MN, ∴∠COP=90°, ∴∠AOC=45°, ∵AC∥OP, ∴∠CAO=∠AOB=45°,∠ACO=∠POE=90°, ∴AC=OC, 连接 AD, ∵BD=OD, ∴AD=OD,AD⊥OB, ∴AD∥OC, ∴四边形 ADOC 是正方形, ∴∠DCO=45°, ∴AC=OD, ∴∠DEO=45°, ∴CD=DE, ∴OC=OE, ∴AC=OE; ②在 Rt△CDO 中, ∵CD2=OC2+OD2,OC=OD, ∴CD2=2OC2, ∴CD= OC, ∴OC=AC= CD, ∴AC+CO= CD+ CD= CD, 故答案为:AC+CO= CD; (2)如图 2,(1)中的结论②成立,理由是: 连接 AD, ∵AB=AO,D 为 OB 的中点, ∴AD⊥OB, ∴∠ADO=90°, ∵∠CDE=90°, ∴∠ADO=∠CDE, ∴∠ADO﹣∠CDO=∠CDE﹣∠CDO, 即∠ADC=∠EDO, ∵∠ADO=∠ACO=90°, ∴∠ADO+∠ACO=180°, ∴A、D、O、C 四点共圆, ∴∠ACD=∠AOB=45°, ∵∠CDE=90°, ∴CD=DE,∠CED=45°, ∴∠CED=∠ACD, ∴△CAD≌△EOD, ∴AC=OE, ∵△CDE 是等腰直角三角形, ∴CE= CD, ∴OE+CO= CD, 即 AC+CO= CD, 所以(1)中的结论②成立; (3)如图 3,结论:OC﹣CA= CD, 理由是:连接 AD,则 AD=OD, 同理:∠ADC=∠EDO, ∵∠CAB+∠CAO=∠CAO+∠AOC=90°, ∴∠CAB=∠AOC, ∵∠DAB=∠AOD=45°, ∴∠DAB﹣∠CAB=∠AOD﹣∠AOC, 即∠DAC=∠DOE, ∴△ACD≌△OED, ∴AC=OE,CD=DE, ∴△CDE 是等腰直角三角形, ∴CE2=2CD2, ∴(OC﹣OE)2=(OC﹣AC)2=2CD2, ∴OC﹣AC= CD, 故答案为:OC﹣AC= CD.查看更多