- 2021-05-10 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
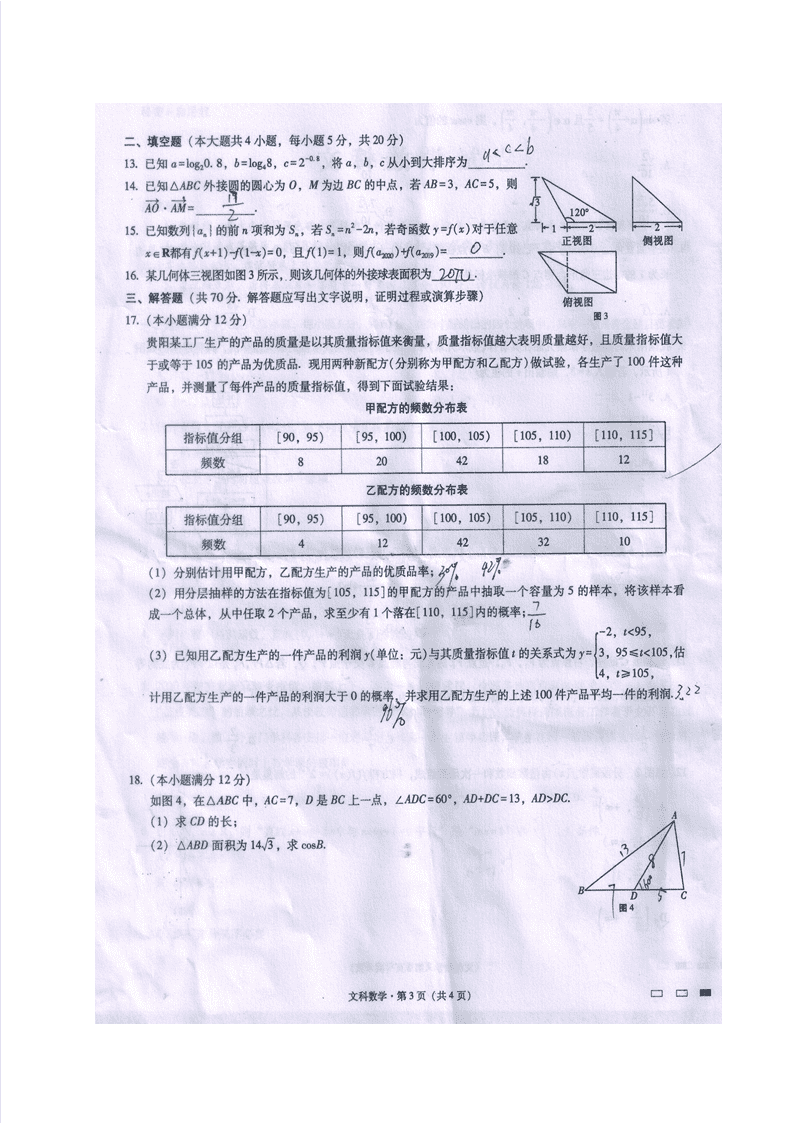
贵州省贵阳市第一中学2020届高三高考适应性月考卷(八)数学(文)试题 图片版 扫描版含答案
贵阳第一中学 2020 届高考适应性月考卷(八) 文科数学参考答案[来源:学科网 ZXXK] 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B C A B A D C B A C D 【解析】 2.由设 iz a b ,代入 | | 2 iz z ,得 3 i4z ,故选 B. 3.∵向量 ( 1 1) ( 2) , , ,a b ,且 a b , ( 1) 2 0 a b ,则 1 或 2,故选 C. 4.A 选项是偶函数且在 (0 ) , 为增;B 选项不是偶函数;C 选项是偶函数,但是在 (0 ) , 不恒 为增函数;D 选项不是偶函数,故选 A. 5.设三个科目分别为 a,b,c,三名学生选择科目的基本事件共有:aaa,bbb,ccc,aab,aba,baa, aac,aca,caa,bba,bab,abb,bbc,bcb,cbb,cca,cac,acc,ccb,cbc,bcc,abc,acb, bca,bac,cab,cba,共 27 种,其中有 6 种满足恰有两名学生选数学,所以概率为 2 9 ,故选 B. 6.若直线 1 0x my 与 1 0nx y 平行,则 1 0mn ,即 1mn ,当 1m , 1n 时,两直 线方程为 1 0x y , 1 0x y ,此时两直线重合,故“直线 1 0x my 与 1 0nx y 平 行”是“ 1mn ”的充分不必要条件,故选 A. 7. 7cos cos cos cos sin si 2n 10 ,故选 D. 8.如图 1,设点 ( 6 )C x x, ,连接 AC AB CO BO, , , ,由△ABC 是边长为1的等边三角形,故四 边 形 AOBC 为 菱 形 , 60 120ACB AOB OAC OBC , , 在 OAC△ 中 , 2 2 2 2 cosOC OA AC OA AC OAC ,可得 2 2 21 1OC 12 1 1 32 , 3OC ,可得 2 23 (6 )x x ,解得 6 2x ,故选 C. 9.由 框 图 得 10(((((((((3 1) 3 1) 3 1) 3 1) 3 1) 3 1) 3 1) 3 1) 3 1) 3 1 3v 图 1 11 11 9 8 1 1 (3 1) 3 13 3 3 1 3 1 2 ,故选 B. 10. 2 1 2 1 2 4 7( ) 2 7 0 2 7 4 0 22f x x x x x x x xx , , 2( ) ( ) 7f a f b a a 24ln a b 7 4lnb b 2 1 2 1 2 1 2 1 2 65( ) 2 7( ) 4ln( ) 4ln 2 4x x x x x x x x ,故选 A. 11.根据题意,作图如图 2 所示,由 2| | 2PF c ,得 1| | 2 2PF a c , 1 3 3| | 2 a cQF , 7 7| |= 2 a cPQ , 2 3| | 2 a cQF , 由 2 2 1cos cosF PQ F PF , 即 2 2 2 2 2 2 | | | | | | 2 | || | PF PQ F Q PF PQ 2 2 2 2 1 1 2 2 1 | | | | | | 2 | || | PF PF F F PF PF ,整 理 得 2 27 12 5 0c ac a , 则 (5 7 )( ) 0a c a c , 得 5 7e , 故 选 C. 12.由图象得函数解析式为 3 1 1( ) 2 1x x xf x x , , , ≥ , 令 ( )f x t ,则 ( ) 2tf t ,当 1t 时, 3 1 2tt , 令 1 23 1 2ty t y , , 1t 其 图 象如 图 3 所 示 . 1t ∴ 时 , 3 1 2tt 无解,当 1t ≥ 时,2 2t t 成立,由 ( ) 1f x ≥ ,得当 1x 时, 有 3 1 1x ≥ ,解得 2 13 x ≤ ;当 1x≥ 时,有 2 1x ≥ ,解得 1x≥ , 综 上, x 的取值范围是 2 3 , ,故选 D. 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 题号 13 14 15 16 答案 a c b 17 2 0 20π 【解析】 13. 0a , 3 12b , 0 1c . 14.如图 4,取 AC 的中点 D , AB 的中点 E ,并连接OD ,OE ,则 OD AC ,OE AB , 21 25 2 2AO AC AC ∴ , AO AB 21 9 2 2AB , 1 25 9 17( )2 4 2AO AM AO AB AC . 15. 2 2nS n n ∵ , 2 3na n ∴ , ( )f x 为周期函数, 4T , 2019( ) (2 2019 3) (4035)f a f f 图 2 图 3 图 4 (3) ( 1) (1) 1f f f , 2020( ) (4037) (1) 1f a f f , 2019 2020( ) ( )f a f a∴ 0 . 16.如图 5,由三视图得几何体为四棱锥 S ABCD ,补为直三棱柱 1SAD S BC ,作 ADS△ 的外接圆圆心为 1O ,半径为 r ,作 1S BC△ 的外接圆圆心为 2O , 1 2O O 的中点 O 为球心, 120SAD ∵ , 2AD , 2SA . 1 2SO r ∴ , 1 1OO , 22 1 5R SO ∴ , 24S R ∴ 20 . 三、解答题(共 70 分.解答应写出文字说明,证 明过程或演算步骤) 17.(本小题满分 12 分) 解:(1)由试验结果知,用甲配方生产的产品中优质品的频率为18 12 0.3100 , 所以用甲配方生产的产品的优质品率的估计值为 30% , …………………………(2 分) 由试验结果知,用乙配方生产的产品中优质品 的频率为 32 10 0.42100 , 所以用 B 配方生产的产品的优质品率的估计值为 42% . ………… ………………(4 分) (2)由题意,∵用分层抽样的方法在指标值为[105 115], 的甲配方的产品中抽取一个容量为 5 的 样本, ∴需在[105 110), 段内抽取 3 个,并分别记为 a ,b , c ; 在[110 115], 段内抽取 2 个,并分别记为 m , n , ………………………………(5 分) 设“从样本中任取 2 个,至少有 1 个在分数段[110 115], 内”为事件 A , 则基本事件共有 ( )m n, ,( )m a, ,( )m b, ,( )m c, ,( )n a, ,( )n b, ,( )n c, ,( )a b, ,( )a c, , ( )b c, ,共 10 种, …………………………………………………………(6 分) 则事件 A 包含的基本事件有 ( )m n, , ( )m a, , ( )m b, , ( )m c, , ( )n a, , ( )n b, , ( )n c, ,共 7 种, ………………………………………………………………(7 分) 7( ) 10P A ∴ . ………………………………………………………(8 分) (3)由条件知,用乙配方生产的一件产品的利润大于 0,当且仅当其质量指标值 95t ≥ ,由试验 结果知,质量指标值 95t ≥ 的频率为 0.96, 所以用乙配方生产的一件产品的利润大于 0 的概率估计值为 0.96, ……………(10 分) 图 5 用乙配方生产的产品平均一件的利润为 1 [4 ( 2) 54 3 42 4] 3.22100 (元). ………………………………………………………………………(12 分) 18.(本小题满分 12 分) 解:(1)由余弦定理得 2 2 2 22 cos60 ( ) 3AC DA DC DA DC DA DC DA DC , 由已知, 13 40DA DC DA DC , , ………………………………………(3 分) 又 AD DC ,所以 5CD . ……………………………………………(6 分) (2)解 法一:由已知, 1 sin120 14 32ABDS AD BD △ ,得 7BD , …………………………………………………………………………………(7 分) 设 AE BC 垂足为 E ,在 ADE△ 中, 4DE , 4 3AE ,………………………(9 分) 所以,在 Rt ABE△ 中, 4 3 11tan cos11 13B B . ………………………………(12 分) 解法二:由已知, 1 sin120 14 32ABDS AD BD △ ,得 7BD , ………………(7 分) 又在 ABD△ 中, 2 2 2 2 cos120 169AB BD DA DA DB , 13AB ∴ , ………………………(10 分) 又在 ABD△ 中,由余弦定理得 11cos 13B . ………………………………(12 分) 19.(本小题满分 12 分) (1)证明:∵是直三棱柱, 1AC BB∴ , …………………………………………(1 分) 又 BD 平面 1AB C , 1AC BD BD BB B ∴ , , …………………………………(3 分) AC ∴ 平面 1 1BB C C , ………………………………………………(4 分) 1B C 平面 1 1 1BB C C AC B C,∴ . ………………………………………………(6 分)[来源:学科网 ZXXK] (2)解:由(1)知 AC 平面 1 1BB C C , AC BC∴ , 2 2 2BC AC AB ,∴ , ……………………………………………(7 分) 设 AP x ,则 1 222 2PACS x x △ , ……………………………………………(8 分) 1 1RtBD B C B BC∵ , △ ∽ Rt 2 3BDC BC BD △ , , , 1 2 3BB ∴ , ……………………………………………………(9 分) 1 1 2 3 22 33 2 3 2B PACV x x ∴ ,∴ , ………………………………………(10 分) 1 3 AP PB ∴ . ……………………………………………………………(12 分) 20.(本小题满分 12 分) 解:(1) 21( ) ( 2)2f x x a x ∵ ,设 3 21 1( ) ( 2)6 2f x x a x b , ………………(1 分) 3(1) 2f a ∴ , 2( ) ag x x ∵ , (1) 2g a ∴ , …………………………………(2 分) 依题意有 (1) (1) 1f g ,且 (1) (1)f g , …………………………………………(3 分) 可得 32 12 1 1 ( 2) 06 2 a a a b , , 解得 1a , 1 3b 或 1 2a , 7 12b , 所以 3 21 1 1( ) 6 2 3f x x x 或 3 21 3 7( ) 6 4 12f x x x . ……………………………(6 分) (2) 21( ) ( 2) 2 ln2F x x a x a x ∵ .[来源:学科网 ZXXK] 1 2 1 2( ) ( ) ( )F x F x a x x , 等价于 2 2 1 1( ) ( )F x ax F x ax . ……………………………………………(7 分) 设 ( ) ( )G x F x ax , 则对任意的 2 10 x x ,等价于 ( ) ( )G x F x ax 在 (0 ) , 上是增函数. ………………………………………………………(8 分) 21( ) 2 ln 22G x x a x x , 可得 22 2 2( ) 2a x x aG x x x x , ……………………………………………(10 分) 依题意有,对任意 0x ,有 2 2 2 0x x a ≥ 恒成立. 由 2 22 2 ( 1) 1a x x x ≤ ,可得 1 2a ≤ . ………………………………………(12 分) 21.(本小题满分 12 分) 解:(1)由已知,圆 E 的半径为| |EQ ,圆 P 的圆心为 P ,半径为 2 2 , 依题意得| | 2 2 | |EP EQ ,即| | | | 2 2 | |EP EQ PQ , ………………………(2 分) 所以点 E 的轨迹是以 P , Q 为焦点的椭圆,其长轴为 2 2 2a , ……………………………………………………………………………(4 分) 曲线 C 的方程是 2 2 12 x y . ……………………………………………(5 分) (2)由 2 2 12 2 x y y kx , , 得 2 2(1 2 ) 8 6 0k x kx , …………………………………(6 分) 由 2 2 264 24(1 2 ) 16 24 0k k k , 解得 6 2k 或 6 2k . ……………………………………………(7 分) 设 1 1( )A x y, , 2 2( )B x y, , 则 1 2 2 8 1 2 kx x k , 1 2 2 6 1 2x x k . ……………………………………………(8 分) 设存在点 (0 )D m, 满足题意,则 1 1 AD y mk x , 2 2 BD y mk x , 所以 1 2 2 1 1 2 1 2 ( ) AD BD y x y x m x xk k x x 1 2 1 2 1 2 2 (2 )( )kx x m x x x x 6 4 (2 ) 3 k k m . ……………………………………………………………(9 分) 要使 AD BDk k 为定值,只需 6 4 (2 ) 6 8 4 2(2 1)k k m k k mk m k 与参数 k 无关, 故 2 1 0m ,解得 1 2m ,当 1 2m 时, 0AD BDk k .[来源:学.科.网] 综上所述,存在点 10 2D , ,使得 AD BDk k 为定值,且定值为 0. …………………………………………………………………………(12 分) 22.(本小题满分 10 分)【选修 4−4:坐标系与参数方程】 解:(1)曲线 1C 的参数方程为 cos ( 0)sin x a a by b , 为参数,, , …………………………………………………………………(1 分) 曲线 3C 的直角坐标方程为 2 2 2x y r ,则其极坐标方程为 r , ……………… …………………………………………………(2 分) 当 r b 或 r a 时,曲线 1C 和曲线 3C 有两个公共点; ………………………(3 分) 当 b r a 时,曲线 1C 和曲线 3C 有四个公共点; …………… ……………………(4 分) 当 0 r b 或 r a 时,曲线 1C 和曲线 3C 没有公共点. …………………………(5 分) (2)设 ( cos sin )M a b , , 1 2(0 ) (0 )B b B b, , , ,[来源:学科网] 则直线 1MB 的方程为 sin cos b by x ba ,∴得 cos 01 sin aP , , …………………(7 分) 同理 2MB 的方程为 sin cos b by x ba ,∴得 cos 01 sin aQ , , ………………………………………………………………(9 分) 2 2 2 2 cos cos cos| | | | 1 sin 1 sin 1 sin a a aOP OQ a ∴ 为定值. ………………………(10 分) 2 3.(本小题满分 10 分)【选修 4−5:不等式选讲】 解:(1)当 0a 时,不等式为 2( ) | | 3 1 0f x x x x , 当 0x≥ 时,不等式为 22 4 0 2x x 或 2x ,又 0x≥ , 2x ∴ ; 当 0x 时,不等式为 2 23 1 0 4 0x x ,此不等式无解, 综合上述,不等式的解集为{ | 2}x x . …………………………………………(5 分) (2)对于 [2 3]x , , | | 2x x a ≥ 恒成立, 即是 2| |x a x ≥ 恒成立, 2x a x ∴ ≥ 或 2x a x ≤ 在 [2 3]x , 时恒成立 2a x x ≤ 或 2a x x ≥ 恒成立, 2x x 在 [2 3]x , 上单调递增,∴当 2x 时有最小值1 1a ≤ , 或 2x x 在 [2 3]x , 上单调递增,∴当 3x 时有最大值 11 3 , 综合上述, 1a≤ 或 11 3a≥ . ……………………………………………………(10 分)查看更多