2019-2020学年吉林省长春外国语学校八年级下学期期末数学试卷 （解析版）

2019-2020学年吉林省长春外国语学校八年级下学期期末数学试卷 （解析版）

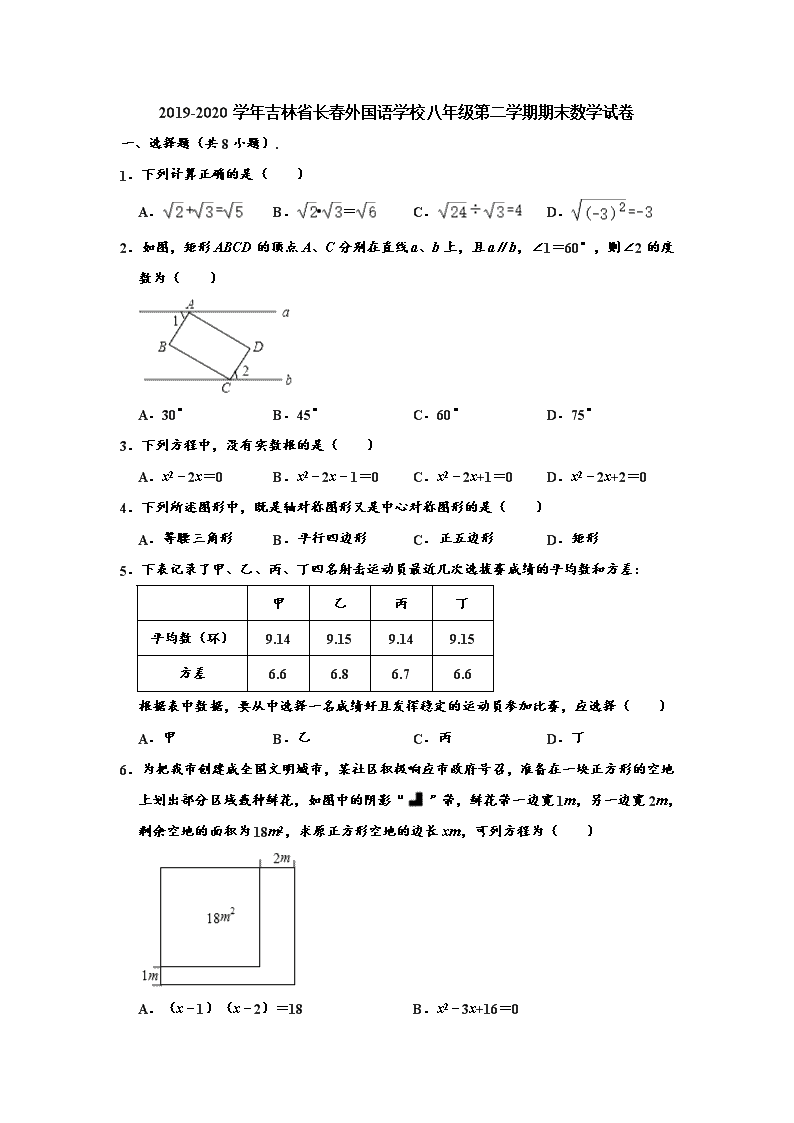
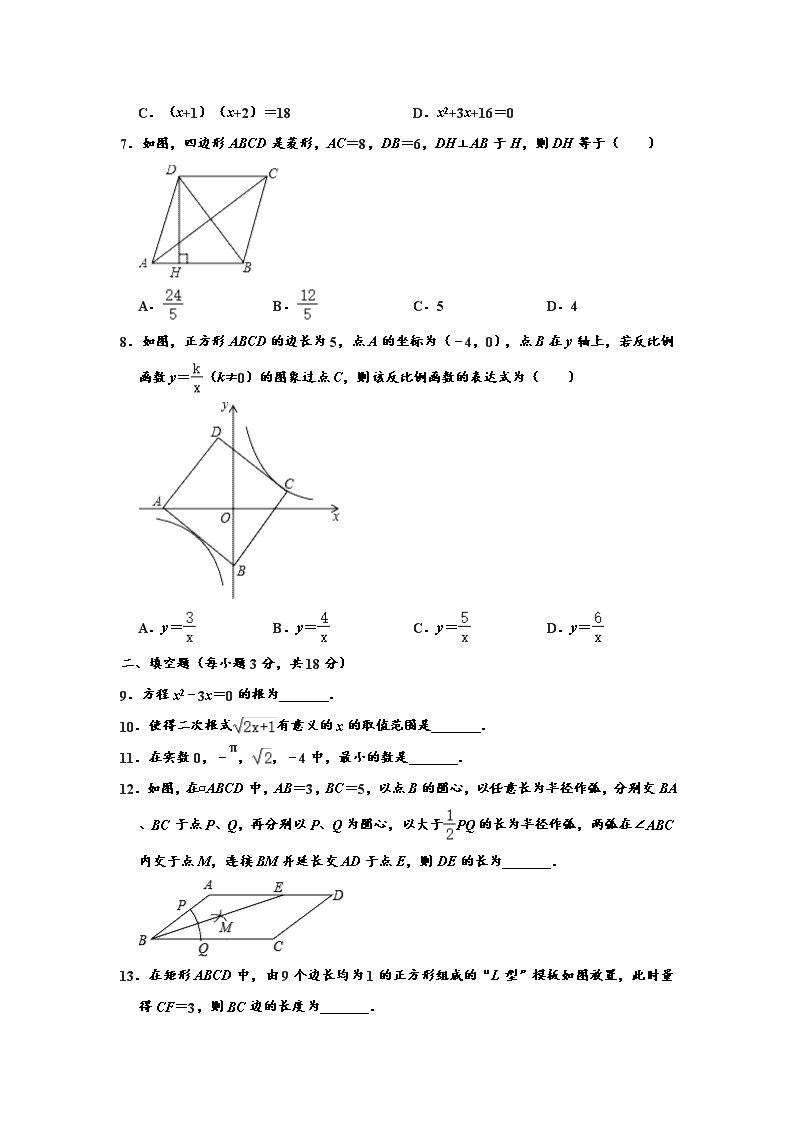
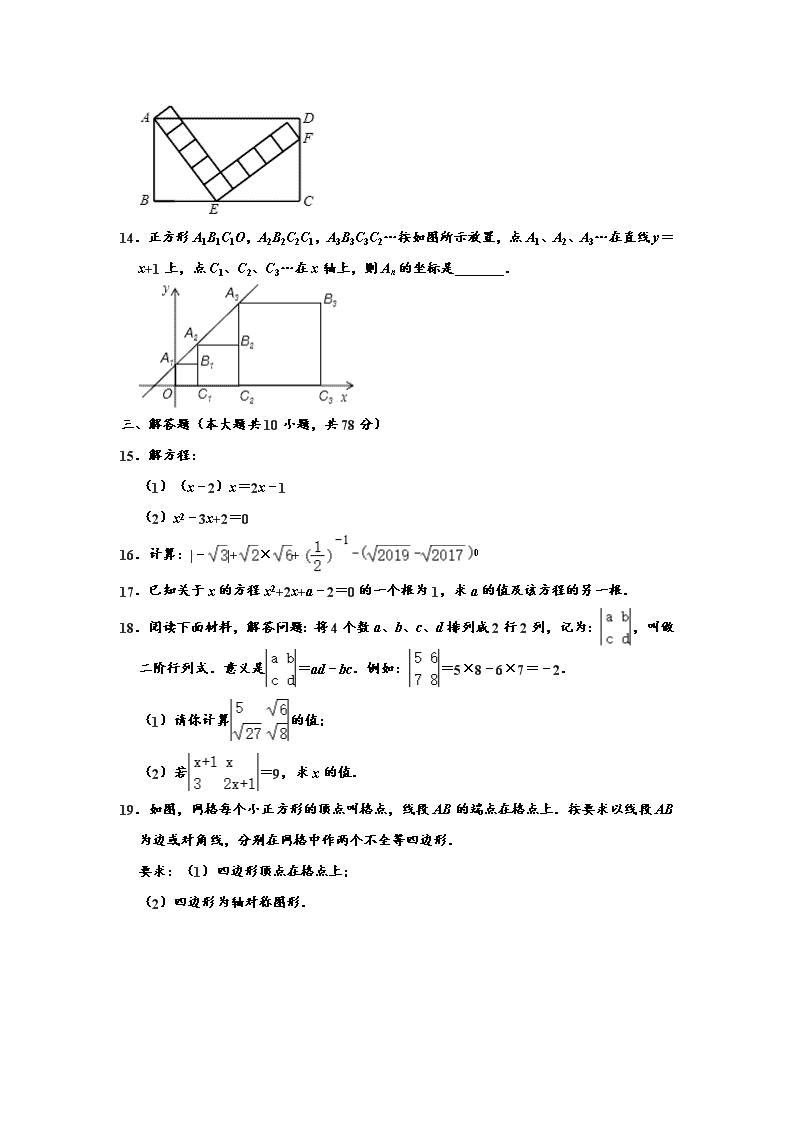
‎2019-2020学年吉林省长春外国语学校八年级第二学期期末数学试卷 一、选择题（共8小题）.‎ ‎1．下列计算正确的是（　　）‎ A． B．•＝ C． D．‎ ‎2．如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1＝60°，则∠2的度数为（　　）‎ A．30° B．45° C．60° D．75°‎ ‎3．下列方程中，没有实数根的是（　　）‎ A．x2﹣2x＝0 B．x2﹣2x﹣1＝‎0 ‎C．x2﹣2x+1＝0 D．x2﹣2x+2＝0‎ ‎4．下列所述图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等腰三角形 B．平行四边形 C．正五边形 D．矩形 ‎5．下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：‎ 甲 乙 丙 丁 平均数（环）‎ ‎9.14‎ ‎9.15‎ ‎9.14‎ ‎9.15‎ 方差 ‎6.6‎ ‎6.8‎ ‎6.7‎ ‎6.6‎ 根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（　　）‎ A．甲 B．乙 C．丙 D．丁 ‎6．为把我市创建成全国文明城市，某社区积极响应市政府号召，准备在一块正方形的空地上划出部分区域栽种鲜花，如图中的阴影“”带，鲜花带一边宽‎1m，另一边宽‎2m，剩余空地的面积为‎18m2‎，求原正方形空地的边长xm，可列方程为（　　）‎ A．（x﹣1）（x﹣2）＝18 B．x2﹣3x+16＝0 ‎ C．（x+1）（x+2）＝18 D．x2+3x+16＝0‎ ‎7．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（　　）‎ A． B． C．5 D．4‎ ‎8．如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数y＝（k≠0）的图象过点C，则该反比例函数的表达式为（　　）‎ A．y＝ B．y＝ C．y＝ D．y＝‎ 二、填空题（每小题3分，共18分）‎ ‎9．方程x2﹣3x＝0的根为　 　．‎ ‎10．使得二次根式有意义的x的取值范围是　 　．‎ ‎11．在实数0，﹣π，，﹣4中，最小的数是　 　．‎ ‎12．如图，在▱ABCD中，AB＝3，BC＝5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为　 　．‎ ‎13．在矩形ABCD中，由9个边长均为1的正方形组成的“L型”模板如图放置，此时量得CF＝3，则BC边的长度为　 　．‎ ‎14．正方形A1B‎1C1O，A2B‎2C2C1，A3B‎3C3C2…按如图所示放置，点A1、A2、A3…在直线y＝x+1上，点C1、C2、C3…在x轴上，则An的坐标是　 　．‎ 三、解答题（本大题共10小题，共78分）‎ ‎15．解方程：‎ ‎（1）（x﹣2）x＝2x﹣1‎ ‎（2）x2﹣3x+2＝0‎ ‎16．计算：|﹣|+×+0‎ ‎17．已知关于x的方程x2+2x+a﹣2＝0的一个根为1，求a的值及该方程的另一根．‎ ‎18．阅读下面材料，解答问题：将4个数a、b、c、d排列成2行2列，记为：，叫做二阶行列式．意义是＝ad﹣bc．例如：＝5×8﹣6×7＝﹣2．‎ ‎（1）请你计算的值；‎ ‎（2）若＝9，求x的值．‎ ‎19．如图，网格每个小正方形的顶点叫格点，线段AB的端点在格点上．按要求以线段AB为边或对角线，分别在网格中作两个不全等四边形．‎ 要求：（1）四边形顶点在格点上；‎ ‎（2）四边形为轴对称图形．‎ ‎20．在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：‎ ‎5640 6430 6520 6798 7325‎ ‎8430 8215 7453 7446 6754‎ ‎7638 6834 7326 6830 8648‎ ‎8753 9450 9865 7290 7850‎ 对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：‎ 步数分组统计表 组别 步数分组 频数 A ‎5500≤x＜6500‎ ‎2‎ B ‎6500≤x＜7500‎ ‎10‎ C ‎7500≤x＜8500‎ m D ‎8500≤x＜9500‎ ‎3‎ E ‎9500≤x＜10500‎ n 请根据以上信息解答下列问题：‎ ‎（1）填空：m＝　 　，n＝　 　；‎ ‎（2）补全频数分布直方图；‎ ‎（3）这20名“健步走运动”团队成员一天行走步数的中位数落在　 　组；‎ ‎（4）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．‎ ‎21．如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．‎ ‎（1）求证：AD＝EC；‎ ‎（2）当∠BAC＝90°时，求证：四边形ADCE是菱形．‎ ‎22．如图所示，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，已知AB＝‎8cm，BC＝‎10cm，‎ 求：（1）BF的长；‎ ‎（2）△ECF的面积．‎ ‎23．数学兴趣小组几名同学到商场调查发现，一种纯牛奶进价为每箱40元，厂家要求售价在40～70元之间，若以每箱70元销售平均每天销售30箱，价格每降低1元平均每天可多销售3箱．‎ ‎（1）现该商场要保证每天盈利900元，同时又要使顾客得到实惠，那么每箱售价为多少元？‎ ‎（2）若每天盈利为W元，请利用配方法直接写出每箱售价为多少元时，每天盈利最多．‎ ‎24．如图，矩形ABCD中，AB＝‎5cm，BC＝‎10cm，动点M从点D出发，按折线DCBAD 方向以‎3cm/s的速度运动，动点N从点D出发，按折线DABCD方向以‎2cm/s的速度运动．点E在线段BC上，且BE＝‎1cm，若M、N两点同时从点D出发，到第一次相遇时停止运动．‎ ‎（1）求经过几秒钟M、N两点停止运动？‎ ‎（2）求点A、E、M、N构成平行四边形时，M、N两点运动的时间；‎ ‎（3）设运动时间为t（s），用含字母t的代数式表示△EMN的面积S（cm2）．‎ 参考答案 一、选择题（每小题3分，共24分）‎ ‎1．下列计算正确的是（　　）‎ A． B．•＝ C． D．‎ ‎【分析】根据二次根式的加减法对A进行判断；根据二次根式的乘法法则对B进行判断；根据二次根式的乘法法则对C进行判断；根据二次根式的性质对D进行判断．‎ 解：A、与不能合并，所以A选项错误；‎ B、原式＝＝，所以B选项正确；‎ C、原式＝＝2，所以C选项错误；‎ D、原式＝|﹣3|＝3，所以D选项错误．‎ 故选：B．‎ ‎2．如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1＝60°，则∠2的度数为（　　）‎ A．30° B．45° C．60° D．75°‎ ‎【分析】首先过点D作DE∥a，由∠1＝60°，可求得∠3的度数，易得∠ADC＝∠2+∠3，继而求得答案．‎ 解：过点D作DE∥a，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠BAD＝∠ADC＝90°，‎ ‎∴∠3＝90°﹣∠1＝90°﹣60°＝30°，‎ ‎∵a∥b，‎ ‎∴DE∥a∥b，‎ ‎∴∠4＝∠3＝30°，∠2＝∠5，‎ ‎∴∠2＝90°﹣30°＝60°．‎ 故选：C．‎ ‎3．下列方程中，没有实数根的是（　　）‎ A．x2﹣2x＝0 B．x2﹣2x﹣1＝‎0 ‎C．x2﹣2x+1＝0 D．x2﹣2x+2＝0‎ ‎【分析】分别计算各方程的根的判别式的值，然后根据判别式的意义判定方程根的情况即可．‎ 解：A、△＝（﹣2）2﹣4×1×0＝4＞0，方程有两个不相等的实数根，所以A选项错误；‎ B、△＝（﹣2）2﹣4×1×（﹣1）＝8＞0，方程有两个不相等的实数根，所以B选项错误；‎ C、△＝（﹣2）2﹣4×1×1＝0，方程有两个相等的实数根，所以C选项错误；‎ D、△＝（﹣2）2﹣4×1×2＝﹣4＜0，方程没有实数根，所以D选项正确．‎ 故选：D．‎ ‎4．下列所述图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等腰三角形 B．平行四边形 C．正五边形 D．矩形 ‎【分析】根据轴对称图形与中心对称图形的概念求解．‎ 解：A、等腰三角形是轴对称图形，不是中心对称图形，故此选项不合题意；‎ B、平行四边形不是轴对称图形，是中心对称图形，故此选项不合题意；‎ C、正五边形是轴对称图形，不是中心对称图形，故此选项不合题意；‎ D、矩形既是轴对称图形又是中心对称图形，故此选项符合题意．‎ 故选：D．‎ ‎5．下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：‎ 甲 乙 丙 丁 平均数（环）‎ ‎9.14‎ ‎9.15‎ ‎9.14‎ ‎9.15‎ 方差 ‎6.6‎ ‎6.8‎ ‎6.7‎ ‎6.6‎ 根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（　　）‎ A．甲 B．乙 C．丙 D．丁 ‎【分析】首先比较平均数，平均数相同时选择方差较小的参加比赛．‎ 解：∵乙和丁的平均数较大，‎ ‎∴从乙和丁中选择一人参加竞赛，‎ ‎∵丁的方差较小，‎ ‎∴选择丁参加比赛，‎ 故选：D．‎ ‎6．为把我市创建成全国文明城市，某社区积极响应市政府号召，准备在一块正方形的空地上划出部分区域栽种鲜花，如图中的阴影“”带，鲜花带一边宽‎1m，另一边宽‎2m，剩余空地的面积为‎18m2‎，求原正方形空地的边长xm，可列方程为（　　）‎ A．（x﹣1）（x﹣2）＝18 B．x2﹣3x+16＝0 ‎ C．（x+1）（x+2）＝18 D．x2+3x+16＝0‎ ‎【分析】可设原正方形的边长为xm，则剩余的空地长为（x﹣1）m，宽为（x﹣2）m．根据长方形的面积公式方程可列出．‎ 解：设原正方形的边长为xm，依题意有 ‎（x﹣1）（x﹣2）＝18，‎ 故选：A．‎ ‎7．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（　　）‎ A． B． C．5 D．4‎ ‎【分析】根据菱形性质求出AO＝4，OB＝3，∠AOB＝90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．‎ 解：∵四边形ABCD是菱形，‎ ‎∴AO＝OC，BO＝OD，AC⊥BD，‎ ‎∵AC＝8，DB＝6，‎ ‎∴AO＝4，OB＝3，∠AOB＝90°，‎ 由勾股定理得：AB＝＝5，‎ ‎∵S菱形ABCD＝，‎ ‎∴，‎ ‎∴DH＝，‎ 故选：A．‎ ‎8．如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数y＝（k≠0）的图象过点C，则该反比例函数的表达式为（　　）‎ A．y＝ B．y＝ C．y＝ D．y＝‎ ‎【分析】过点C作CE⊥y轴于E，根据正方形的性质可得AB＝BC，∠ABC＝90°，再根据同角的余角相等求出∠OAB＝∠CBE，然后利用“角角边”证明△ABO和△BCE全等，根据全等三角形对应边相等可得OA＝BE＝4，CE＝OB＝3，再求出OE，然后写出点C的坐标，再把点C的坐标代入反比例函数解析式计算即可求出k的值．‎ 解：如图，过点C作CE⊥y轴于E，在正方形ABCD中，AB＝BC，∠ABC＝90°，‎ ‎∴∠ABO+∠CBE＝90°，‎ ‎∵∠OAB+∠ABO＝90°，‎ ‎∴∠OAB＝∠CBE，‎ ‎∵点A的坐标为（﹣4，0），‎ ‎∴OA＝4，‎ ‎∵AB＝5，‎ ‎∴OB＝＝3，‎ 在△ABO和△BCE中，‎ ‎，‎ ‎∴△ABO≌△BCE（AAS），‎ ‎∴OA＝BE＝4，CE＝OB＝3，‎ ‎∴OE＝BE﹣OB＝4﹣3＝1，‎ ‎∴点C的坐标为（3，1），‎ ‎∵反比例函数y＝（k≠0）的图象过点C，‎ ‎∴k＝xy＝3×1＝3，‎ ‎∴反比例函数的表达式为y＝．‎ 故选：A．‎ 二、填空题（每小题3分，共18分）‎ ‎9．方程x2﹣3x＝0的根为　x1＝0，x2＝3　．‎ ‎【分析】根据所给方程的系数特点，可以对左边的多项式提取公因式，进行因式分解，然后解得原方程的解．‎ 解：因式分解得，x（x﹣3）＝0，‎ 解得，x1＝0，x2＝3．‎ 故答案为：x1＝0，x2＝3．‎ ‎10．使得二次根式有意义的x的取值范围是　x≥﹣　．‎ ‎【分析】根据被开方数大于等于0列式计算即可得解．‎ 解：根据题意得，2x+1≥0，‎ 解得x≥﹣．‎ 故答案为：x≥﹣．‎ ‎11．在实数0，﹣π，，﹣4中，最小的数是　﹣4　．‎ ‎【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．‎ 解：根据有理数比较大小的方法，可得 ‎﹣4＜﹣π＜0＜，‎ ‎∴在﹣4，0，，﹣π中最小的数是﹣4，‎ 故答案为：﹣4．‎ ‎12．如图，在▱ABCD中，AB＝3，BC＝5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为　2　．‎ ‎【分析】根据作图过程可得得BE平分∠ABC；再根据角平分线的性质和平行四边形的性质可证明∠AEB＝∠CBE，证出AE＝AB＝3，即可得出DE的长．，‎ 解：根据作图的方法得：BE平分∠ABC，‎ ‎∴∠ABE＝∠CBE ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，AD＝BC＝5，‎ ‎∴∠AEB＝∠CBE，‎ ‎∴∠ABE＝∠AEB，‎ ‎∴AE＝AB＝3，‎ ‎∴DE＝AD﹣AE＝5﹣3＝2；‎ 故答案为：2．‎ ‎13．在矩形ABCD中，由9个边长均为1的正方形组成的“L型”模板如图放置，此时量得CF＝3，则BC边的长度为　7　．‎ ‎【分析】连接AF，作GH⊥AE于点H，则有AE＝EF＝HG＝4，FG＝2，AH＝2，根据矩形的性质及勾股定理即可求得 解：由图可知，AE＝EF＝5，‎ 根据勾股定理，易得CE＝4，‎ 由题可知AE⊥EF，易得△ABE≌△ECF，‎ 即BE＝CF＝3，即BC＝3+4＝7，‎ 故答案为：7‎ ‎14．正方形A1B‎1C1O，A2B‎2C2C1，A3B‎3C3C2…按如图所示放置，点A1、A2、A3…在直线y＝x+1上，点C1、C2、C3…在x轴上，则An的坐标是　（2n﹣1﹣1，2n﹣1），　．‎ ‎【分析】先求出A1、A2、A3的坐标，找出规律，即可得出答案．‎ 解：∵直线y＝x+1和y轴交于A1，‎ ‎∴A1的坐标（0，1），‎ 即OA1＝1，‎ ‎∵四边形C1OA1B1是正方形，‎ ‎∴OC1＝OA1＝1，‎ 把x＝1代入y＝x+1得：y＝2，‎ ‎∴A2的坐标为（1，2），‎ 同理A3的坐标为（3，4），‎ ‎…‎ An的坐标为（2n﹣1﹣1，2n﹣1），‎ 故答案为：（2n﹣1﹣1，2n﹣1），‎ 三、解答题（本大题共10小题，共78分）‎ ‎15．解方程：‎ ‎（1）（x﹣2）x＝2x﹣1‎ ‎（2）x2﹣3x+2＝0‎ ‎【分析】（1）根据配方法即可求出答案；‎ ‎（2）根据因式分解法即可求出答案．‎ 解：（1）∵（x﹣2）x＝2x﹣1，‎ ‎∴x2﹣2x＝2x﹣1‎ ‎∴x2﹣4x＝﹣1，‎ ‎∴x2﹣4x+4＝3，‎ ‎∴（x﹣2）2＝3，‎ ‎∴x＝2±；‎ ‎（2）∵x2﹣3x+2＝0，‎ ‎∴（x﹣1）（x﹣2）＝0，‎ ‎∴x＝1或x＝2；‎ ‎16．计算：|﹣|+×+0‎ ‎【分析】直接利用负指数幂的性质以及零指数幂的性质和二次根式的性质分别化简得出答案．‎ 解：原式＝+2+2﹣1‎ ‎＝3+1．‎ ‎17．已知关于x的方程x2+2x+a﹣2＝0的一个根为1，求a的值及该方程的另一根．‎ ‎【分析】将x＝1代入原方程可求出a值，再由根与系数的关系结合方程的一根为1可求出方程的另一根．‎ 解：将x＝1代入原方程，得：1+2+a﹣2＝0，‎ 解得：a＝﹣1．‎ 设方程的另一根为x1，‎ 则1+x1＝﹣2，‎ 解得：x1＝﹣3．‎ ‎∴a的值为﹣1，方程的另一个根为﹣3．‎ ‎18．阅读下面材料，解答问题：将4个数a、b、c、d排列成2行2列，记为：，叫做二阶行列式．意义是＝ad﹣bc．例如：＝5×8﹣6×7＝﹣2．‎ ‎（1）请你计算的值；‎ ‎（2）若＝9，求x的值．‎ ‎【分析】（1）根据所给公式代入相应数据进行计算即可；‎ ‎（2）根据所给公式可得方程（x+1）（2x+1）﹣3x＝9，然后再去括号、合并同类项、移项、系数化1进行解方程即可得到x的值．‎ 解：（1）原式＝5×﹣×＝10﹣9＝；‎ ‎（2）由题可得：‎ ‎（x+1）（2x+1）﹣3x＝9，‎ ‎2x2+x+2x+1﹣3x＝9，‎ ‎2x2+1＝9，‎ ‎2x2＝8，‎ x2＝4，‎ x＝±2，‎ 则x1＝2，x2＝﹣2．‎ ‎19．如图，网格每个小正方形的顶点叫格点，线段AB的端点在格点上．按要求以线段AB为边或对角线，分别在网格中作两个不全等四边形．‎ 要求：（1）四边形顶点在格点上；‎ ‎（2）四边形为轴对称图形．‎ ‎【分析】以AB为边画一个矩形和以AB为对角线画正方形即可．‎ 解：如图，四边形ABCD和四边形AEBF为所作．‎ ‎20．在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：‎ ‎5640 6430 6520 6798 7325‎ ‎8430 8215 7453 7446 6754‎ ‎7638 6834 7326 6830 8648‎ ‎8753 9450 9865 7290 7850‎ 对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：‎ 步数分组统计表 组别 步数分组 频数 A ‎5500≤x＜6500‎ ‎2‎ B ‎6500≤x＜7500‎ ‎10‎ C ‎7500≤x＜8500‎ m D ‎8500≤x＜9500‎ ‎3‎ E ‎9500≤x＜10500‎ n 请根据以上信息解答下列问题：‎ ‎（1）填空：m＝　4　，n＝　1　；‎ ‎（2）补全频数分布直方图；‎ ‎（3）这20名“健步走运动”团队成员一天行走步数的中位数落在　B　组；‎ ‎（4）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．‎ ‎【分析】（1）根据题目中的数据即可直接确定m和n的值；‎ ‎（2）根据（1）的结果即可直接补全直方图；‎ ‎（3）根据中位数的定义直接求解；‎ ‎（4）利用总人数乘以对应的比例即可求解．‎ 解：（1）m＝4，n＝1．‎ 故答案是：4，1；‎ ‎（2）‎ ‎；‎ ‎（3）行走步数的中位数落在B组，‎ 故答案是：B；‎ ‎（4）一天行走步数不少于7500步的人数是：120×＝48（人）．‎ 答：估计一天行走步数不少于7500步的人数是48人．‎ ‎21．如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．‎ ‎（1）求证：AD＝EC；‎ ‎（2）当∠BAC＝90°时，求证：四边形ADCE是菱形．‎ ‎【分析】（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形，即得AD＝CE；‎ ‎（2）由∠BAC＝90°，AD是边BC上的中线，即得AD＝BD＝CD，证得四边形ADCE是平行四边形，即证；‎ ‎【解答】证明：（1）∵DE∥AB，AE∥BC，‎ ‎∴四边形ABDE是平行四边形，‎ ‎∴AE∥BD，且AE＝BD 又∵AD是BC边的中线，‎ ‎∴BD＝CD，‎ ‎∴AE＝CD，‎ ‎∵AE∥CD，‎ ‎∴四边形ADCE是平行四边形，‎ ‎∴AD＝EC；‎ ‎（2）∵∠BAC＝90°，AD是斜边BC上的中线，‎ ‎∴AD＝BD＝CD，‎ 又∵四边形ADCE是平行四边形，‎ ‎∴四边形ADCE是菱形．‎ ‎22．如图所示，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，已知AB＝‎8cm，BC＝‎10cm，‎ 求：（1）BF的长；‎ ‎（2）△ECF的面积．‎ ‎【分析】（1）因为点F为点D的折后的落点，所以△AFE≌△ADE，由此可得AF＝AD＝‎10cm，在△ABF中利用勾股定理，可得BF的值，‎ ‎（2）先求出DE的长，进而求出CE的长，利用三角形的面积公式即可求出△ECF的面积．‎ 解：（1）由题意可得：△AEF≌△AED ‎∴AF＝AD＝‎10cm，‎ ‎∵∠ABF＝90°，AB＝‎8cm，‎ ‎∴在△ABF中，由勾股定理得BF＝＝＝‎6cm；‎ ‎（2）设DE长xcm，则EF也长xcm，‎ ‎∴EC长（8﹣x）cm．‎ 由（1）得：CF＝BC﹣BF＝‎4cm．‎ 在△CEF中，由勾股定理CE2+CF2＝EF2‎ 列方程得：（8﹣x）2+42＝x2‎ 解得x＝‎5cm．‎ ‎∴CE＝8﹣5＝‎3cm，‎ ‎∴S△ECF＝×CF•CE＝×4×3＝‎6cm2．‎ ‎23．数学兴趣小组几名同学到商场调查发现，一种纯牛奶进价为每箱40元，厂家要求售价在40～70元之间，若以每箱70元销售平均每天销售30箱，价格每降低1元平均每天可多销售3箱．‎ ‎（1）现该商场要保证每天盈利900元，同时又要使顾客得到实惠，那么每箱售价为多少元？‎ ‎（2）若每天盈利为W元，请利用配方法直接写出每箱售价为多少元时，每天盈利最多．‎ ‎【分析】（1）设每箱售价为x元，根据每箱（售价﹣进价）×销售量等于利润900元，解一元二次方程即可；‎ ‎（2）将（1）中利润的表达式，化简并配方，即可得答案．‎ ‎【解答】（1）解：设每箱售价为x元，根据题意得：‎ ‎（x﹣40）[30+3（70﹣x）]＝900‎ 化简得：x2﹣120x+3500＝0‎ 解得：x1＝50或x2＝70（不合题意，舍去）‎ ‎∴x＝50‎ 答：当每箱牛奶售价为50元时，平均每天的利润为900元．‎ ‎（2）由（1）可知，‎ w＝（x﹣40）[30+3（70﹣x）]‎ ‎＝﹣3x2+360x﹣9600‎ ‎＝﹣3（x﹣60）2+1200‎ ‎∴当x＝60时，每天盈利最多．‎ 答：每箱售价为60元时，每天盈利最多．‎ ‎24．如图，矩形ABCD中，AB＝‎5cm，BC＝‎10cm，动点M从点D出发，按折线DCBAD方向以‎3cm/s的速度运动，动点N从点D出发，按折线DABCD方向以‎2cm/s的速度运动．点E在线段BC上，且BE＝‎1cm，若M、N两点同时从点D出发，到第一次相遇时停止运动．‎ ‎（1）求经过几秒钟M、N两点停止运动？‎ ‎（2）求点A、E、M、N构成平行四边形时，M、N两点运动的时间；‎ ‎（3）设运动时间为t（s），用含字母t的代数式表示△EMN的面积S（cm2）．‎ ‎【分析】（1）由题意可得：M、N两点同时从点D出发，到第一次相遇时共运动了：2（5+10）＝30（cm），则可得t＝30÷（2+3）＝6；‎ ‎（2）由题意知，当点N在AD边上运动，点M在BC边上运动时，点A、E、M、N才可能组成平行四边形，然后设经过t秒，四点可组成平行四边形，①当构▱成▱AEMN时，10﹣2t＝14﹣3t，②当构成▱AMEN时，10﹣2t＝3t﹣14，继而求得答案；‎ ‎（3）分别从当 0＜t＜时，当≤t＜时，当＜t≤5时，当5＜t＜6时，去分析求解即可求得答案．‎ 解：（1）∵矩形ABCD中，AB＝‎5cm，BC＝‎10cm，‎ ‎∴M、N两点同时从点D出发，到第一次相遇时共运动了：2（5+10）＝30（cm），‎ ‎∴t＝30÷（2+3）＝6 （s）‎ 答：经过6 s两点相遇．‎ ‎（2）由题意知，当点N在AD边上运动，点M在BC边上运动时，点A、E、M、N才可能组成平行四边形，‎ 设经过t秒，四点可组成平行四边形，‎ ‎①当构成▱AEMN时，10﹣2t＝14﹣3t，‎ 解得t＝4；‎ ‎②当构成▱AMEN时，10﹣2t＝3t﹣14，‎ 解得t＝4.8；‎ 答：当点A、E、M、N构成平行四边形时，M、N两点运动的时间为4s或4.8s．‎ ‎（3）如图（1），当0＜t＜时，S＝S梯形CDNE﹣S△DMN﹣S△CEM＝×（2t+9）×5﹣×2t×3t﹣×9×（5﹣3t）＝﹣3t2+t；‎ 如图（2），当≤t＜时，S＝S△EMN＝EM•CD＝×（14﹣3t）×5＝35﹣t；‎ 如图（3），当＜t≤5时，S＝S△EMN＝×（3t﹣14）×5＝t﹣35；‎ 如图（4），当5＜t＜6时，S＝S△EMN＝MN•BE＝×（30﹣2t﹣3t）×1＝15﹣t．‎