- 2021-05-10 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习对数的概念课件(12张)(全国通用)
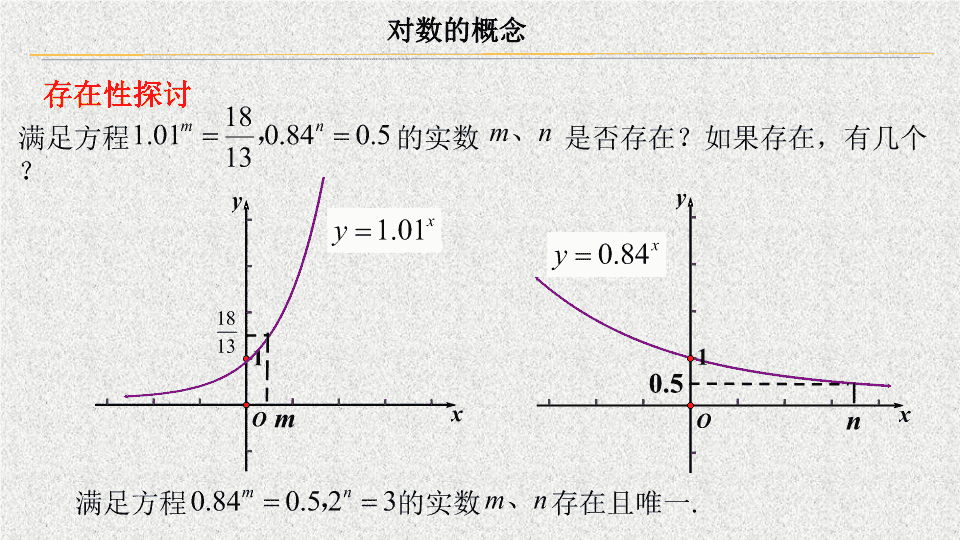
对数的概念 情境问题 ( 1 ) 经过 20 年以后我国人口数是多少? ( 2 )经过多少年我国的人口数可以达到 18 亿 ? 截止到 1999 年底,我国人口约 13 亿.如果今后能将人口年平均增长率控制在 1% ,则根据前面学习的知识我们可以得到我国人口数 与所经过年数 之间的关系为: . 问题 请你根据我国人口数与所经过年数的关系设计一个问题 . 对数的概念 上面 问题 的本质就是在 (其中 且 )中已知两个量求第三个量: 1. 已知 求 . 例如 2. 已知 求 . 例如 问题探源 对数的概念 满足方程 的实数 是否存在?如果存在,有几个? 存在性探讨 0.5 m n 满足方程 的实数 存在且唯一 . 对数的概念 更一般地,在 (其中 且 )中,已知 、 , 是否存在呢? 存在性探讨 对于 (其中 且 ),已知 求 , 是唯一存在的 . 对数的概念 表示方法 通过上述探究,我们知道满足方程 的实数 是唯一存在的,那么它该怎么表示呢? 以 为例, 是一种新的数,且与 0.84 和 0.5 都有关系,于是我们引入新的符号 表示 ,这种新数叫做对数 . 一般地,如果 (其中 且 ) , 那么数 叫做以 为底 的 对数 , 对数的概念 通常我们把以 10 为底的对数叫做 常用对数 ,并把 log 10 N 记为 lg N . 由 可知 是以 2 为底 3 的对数, 由 可知 是以 0.84 为底 0.5 的对数, 另外,科学技术中常用以无理数 e=2.71828 … 为底数的对数,以 e 为底的对数称为 自然对数 ,并把 log e N 记为 ln N . 记作 , 其中 叫做对数的 底数 , 叫做 真数 . 对数的概念 记作 记作 对数的概念 且 指数 对数 底数 幂 真数 对数值可以是任意实数 对数的真数必须是正数 对数的概念 对数的概念 例 1 将下列指数式化为对数式、对数式化为指数式: 对数的概念 变式训练 1 求下列各式中的 对数的概念 追问 1 当 时,把 中的 换成 结论还成立吗? 把 中的 换成 即 呢? 且 小结 1 当 时, 且 对数的概念 追问 2 我们知道正数都有对数,那么当 时, 小结 2 当 时, 且 且 设 ,则: 当 且 时, 即 在定义域内单调 解析: 设 ,则: 解析: 对数的概念 例 2 求下列各式的值:查看更多