- 2021-05-10 发布 |
- 37.5 KB |
- 24页

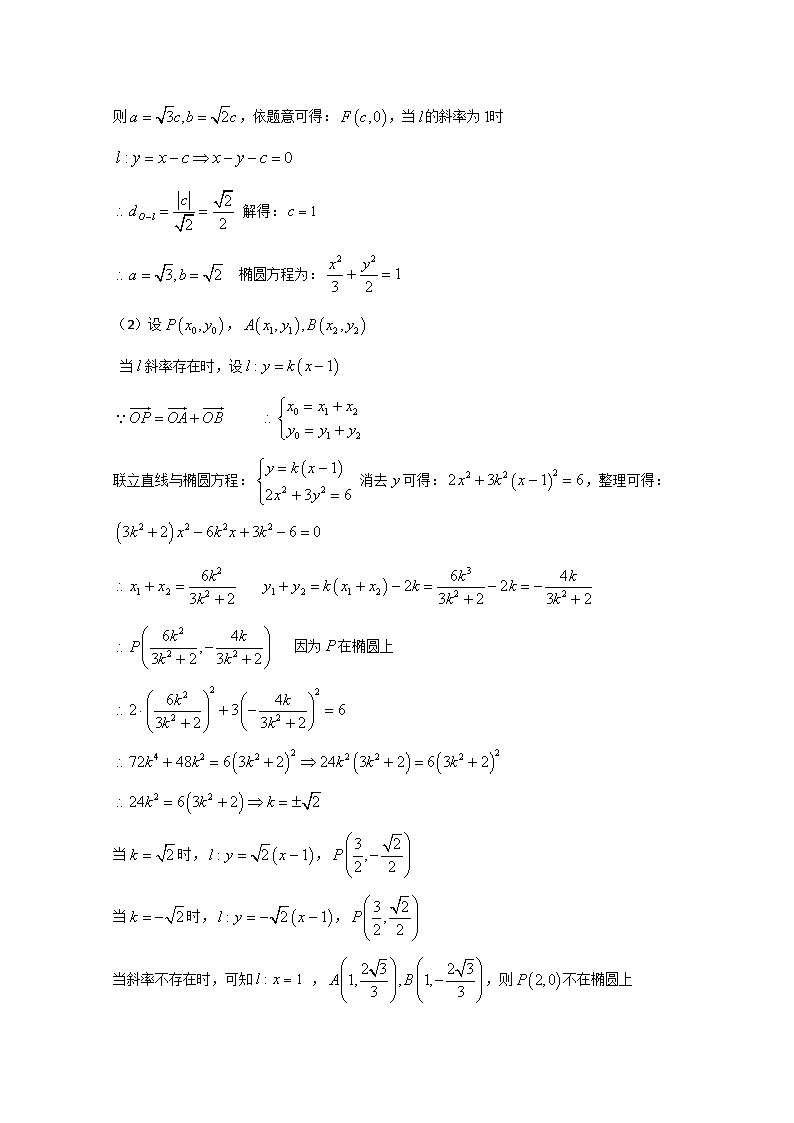

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习存在性问题学案(全国通用)
微专题76 圆锥曲线中的存在性问题 一、基础知识 1、在处理圆锥曲线中的存在性问题时,通常先假定所求的要素(点,线,图形或是参数)存在,并用代数形式进行表示。再结合题目条件进行分析,若能求出相应的要素,则假设成立;否则即判定不存在 2、存在性问题常见要素的代数形式:未知要素用字母代替 (1)点:坐标 (2)直线:斜截式或点斜式(通常以斜率为未知量) (3)曲线:含有未知参数的曲线标准方程 3、解决存在性问题的一些技巧: (1)特殊值(点)法:对于一些复杂的题目,可通过其中的特殊情况,解得所求要素的必要条件,然后再证明求得的要素也使得其它情况均成立。 (2)核心变量的选取:因为解决存在性问题的核心在于求出未知要素,所以通常以该要素作为核心变量,其余变量作为辅助变量,必要的时候消去。 (3)核心变量的求法: ①直接法:利用条件与辅助变量直接表示出所求要素,并进行求解 ②间接法:若无法直接求出要素,则可将核心变量参与到条件中,列出关于该变量与辅助变量的方程(组),运用方程思想求解。 二、典型例题: 例1:已知椭圆的离心率为,过右焦点的直线与相交于两点,当的斜率为时,坐标原点到的距离为。 (1)求的值 (2)上是否存在点,使得当绕旋转到某一位置时,有成立?若存在,求出所有的的坐标和的方程,若不存在,说明理由 解:(1) 则,依题意可得:,当的斜率为时 解得: 椭圆方程为: (2)设, 当斜率存在时,设 联立直线与椭圆方程: 消去可得:,整理可得: 因为在椭圆上 当时,, 当时,, 当斜率不存在时,可知 ,,则不在椭圆上 综上所述:,或, 例2:过椭圆的右焦点的直线交椭圆于两点,为其左焦点,已知的周长为8,椭圆的离心率为 (1)求椭圆的方程 (2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆恒有两个交点,且?若存在,求出该圆的方程;若不存在,请说明理由 解:(1)由的周长可得: 椭圆 (2)假设满足条件的圆为,依题意,若切线与椭圆相交,则圆应含在椭圆内 若直线斜率存在,设, 与圆相切 即 联立方程: 对任意的均成立 将代入可得: 存在符合条件的圆,其方程为: 当斜率不存在时,可知切线为 若,则 符合题意 若,同理可得也符合条件 综上所述,圆的方程为: 例3:已知椭圆的左右焦点分别为,短轴两个端点为,且四边形是边长为2的正方形 (1)求椭圆的方程 (2)若分别是椭圆长轴的左,右端点,动点满足,连接,交椭圆于点,证明是定值 (3)在(2)的条件下,试问轴上是否存在异于点的定点,使得以为直径的圆恒过直线的交点。若存在,求出点的坐标;若不存在,请说明理由 解:(1)四边形是边长为2的正方形 可得: 椭圆方程为 (2)由椭圆方程可得:,由可设, ,与椭圆方程联立可得: 由韦达定理可知: 代入直线可得: 设 若以为直径的圆恒过直线的交点,则 恒成立, 存在定点 例4:设为椭圆的右焦点,点在椭圆上,直线与以原点为圆心,以椭圆的长半轴长为半径的圆相切 (1)求椭圆的方程 (2)过点的直线与椭圆相交于两点,过点且平行于的直线与椭圆交于另一点,问是否存在直线,使得四边形的对角线互相平分?若存在,求出的方程;若不存在,说明理由 解:(1)与圆相切 将代入椭圆方程可得: 椭圆方程为: (2)由椭圆方程可得: 设直线,则 联立直线与椭圆方程: 消去可得: 同理: 联立直线与椭圆方程: 消去可得: 因为四边形的对角线互相平分 四边形为平行四边形 解得: 存在直线时,四边形的对角线互相平分 例5:椭圆的左右焦点分别为,右顶点为,为椭圆上任意一点,且的最大值的取值范围是,其中 (1)求椭圆的离心率的取值范围 (2)设双曲线以椭圆的焦点为顶点,顶点为焦点,是双曲线在第一象限上任意一点,当取得最小值时,试问是否存在常数,使得恒成立?若存在,求出的值;若不存在,请说明理由 解:(1)设 由可得:代入可得: (2)当时,可得: 双曲线方程为,,设, 当轴时, 因为 所以,下面证明对任意点均使得成立 考虑 由双曲线方程,可得: 结论得证 时,恒成立 例6:如图,椭圆的离心率是,过点的动直线与椭圆相交于两点,当直线平行于轴时,直线被椭圆截得的线段长为 (1)求椭圆的方程 (2)在平面直角坐标系中,是否存在与点不同的定点,使得对于任意直线,恒成立?若存在,求出点的坐标;若不存在,请说明理由 解:(1) 椭圆方程为 由直线被椭圆截得的线段长为及椭圆的对称性可得: 点在椭圆上 椭圆方程为 (2)当与轴平行时,由对称性可得: 即 在的中垂线上,即位于轴上,设 当与轴垂直时,则 可解得或 不重合 下面判断能否对任意直线均成立 若直线的斜率存在,设, 联立方程可得: 由可想到角平分线公式,即只需证明平分 只需证明 ① 因为在直线上,代入①可得: 联立方程可得: 成立 平分 由角平分线公式可得: 例7:椭圆的上顶点为,是上的一点,以为直径的圆经过椭圆的右焦点 (1)求椭圆的方程 (2)动直线与椭圆有且只有一个公共点,问:在轴上是否存在两个定点,它们到直线的距离之积等于1?若存在,求出这两个定点的坐标;如果不存在,请说明理由 解:由椭圆可知: 为直径的圆经过 由在椭圆上,代入椭圆方程可得: 椭圆方程为 (2)假设存在轴上两定点, 设直线 所以依题意: ① 因为直线与椭圆相切,联立方程: 由直线与椭圆相切可知 化简可得:,代入①可得: ,依题意可得:无论为何值,等式均成立 所以存在两定点: 例8:已知椭圆的左右焦点分别为,点是上任意一点,是坐标原点,,设点的轨迹为 (1)求点的轨迹的方程 (2)若点满足:,其中是上的点,且直线的斜率之积等于,是否存在两定点,使得为定值?若存在,求出定点的坐标;若不存在,请说明理由 (1)设点的坐标为,点的坐标为,则 由椭圆方程可得: 且 代入到可得: (2)设点, 设直线的斜率分别为,由已知可得: 考虑 是上的点 即的轨迹方程为,由定义可知,到椭圆焦点的距离和为定值 为椭圆的焦点 所以存在定点 例9:椭圆的焦点到直线的距离为,离心率为,抛物线的焦点与椭圆的焦点重合,斜率为的直线过的焦点与交于,与交于 (1)求椭圆及抛物线的方程 (2)是否存在常数,使得为常数?若存在,求出的值;若不存在,请说明理由 解:(1)设的公共焦点为 (2)设直线, 与椭圆联立方程: 直线与抛物线联立方程: 是焦点弦 若为常数,则 例10:如图,在平面直角坐标系中,椭圆的离心率为,直线与轴交于点,与椭圆交于两点,当直线垂直于轴且点为椭圆 的右焦点时,弦的长为 (1)求椭圆的方程 (2)是否存在点,使得为定值?若存在,请求出点的坐标,并求出该定值;若不存在,请说明理由 解:(1)依题意可得: 当与轴垂直且为右焦点时,为通径 (2)思路:本题若直接用用字母表示坐标并表示,则所求式子较为复杂,不易于计算定值与的坐标。因为要满足所有直线,所以考虑先利用特殊情况求出点及定值,再取判定(或证明)该点在其它直线中能否使得为定值。 解:(2)假设存在点,设 若直线与轴重合,则 若直线与轴垂直,则关于轴对称 设,其中,代入椭圆方程可得: ,可解得: 若存在点,则。若,设 设,与椭圆联立方程可得:,消去可得: ,同理: 代入可得: 所以为定值,定值为 若,同理可得为定值 综上所述:存在点,使得为定值 三、历年好题精选 1、已知中心在原点,焦点在坐标轴上的椭圆过点,离心率为,过直线上一点引椭圆的两条切线,切点分别是 (1)求椭圆的方程 (2)若在椭圆上的任一点处的切线方程是,求证:直线恒过定点,并求出定点的坐标 (3)是否存在实数,使得恒成立?(点为直线恒过的定点),若存在,求出的值;若不存在,请说明理由 2、已知椭圆的一个焦点与抛物线的焦点重合,是椭圆上的一点 (1)求椭圆的方程 (2)设分别是椭圆的左右顶点,是椭圆上异于的两个动点,直线的斜率之积为,设与的面积分别为,请问:是否存在常数,使得恒成立?若存在,求出的值,若不存在,请说明理由 3、已知椭圆经过点,离心率为,左,右焦点分别为和 (1)求椭圆的方程 (2)设椭圆与轴负半轴交点为,过点作斜率为的直线,交椭圆于两点(在之间),为中点,并设直线的斜率为 ① 证明:为定值 ② 是否存在实数,使得?如果存在,求直线的方程;如果不存在,请说明理由 4、已知圆,定点,点为圆上的动点,点在上,点在上,且满足 (1)求点的轨迹的方程 (2)过点作直线,与曲线交于两点,是坐标原点,设,是否存在这样的直线,使得四边形的对角线相等(即)?若存在,求出直线的方程;若不存在,试说明理由 5、(2014,福建)已知双曲线的两条渐近线分别为, (1)求双曲线的离心率 (2)如图,为坐标原点,动直线分别交直线于两点(分别在第一、四象限),且的面积恒为8,试探究:是否存在总与直线有且只有一个公共点的双曲线?若存在,求出双曲线的方程;若不存在请说明理由 习题答案: 1、解析:(1) 椭圆过点 ,再由可解得: 椭圆方程为: (2)设切点坐标为,直线上一点,依题意可得: 两条切线方程为: ,由切线均过可得: 均在直线上 因为两点唯一确定一条直线 ,即过定点,即点的坐标为 (3) 联立方程: ,不妨设 ,使得恒成立 2、解析:(1)抛物线的焦点为 依题意可知: 椭圆方程为: (2)由(1)可得:,若直线斜率存在 设, 到直线的距离 到直线的距离 联立方程: (*) ,代入到(*)可得: 或 当时,,交点与重合,不符题意 ,代入到可得: ,即 3、解:(1)依题意可知:可得: 椭圆方程为:,代入可得: 椭圆方程为: (2)① 证明:设,线段的中点 设直线的方程为:,联立方程: 化为: 由解得: 且 ② 假设存在实数,使得,则 即 因为在椭圆上,所以,矛盾 所以不存在符合条件的直线 4、解析:(1)由可得为的中点,且 为的中垂线 点的轨迹是以为焦点的椭圆,其半长轴长为,半焦距 轨迹方程为: (2)因为 四边形为平行四边形 若,则四边形为矩形,即 ① 若直线的斜率不存在,则 联立方程:,即 故不符合要求 ② 若直线的斜率存在,设 由 ,解得: 所以存在或,使得四边形的对角线相等 5、解析:(1)由双曲线方程可知,渐近线方程为 (2)若直线不与轴垂直,设 联立方程: ,同理可得 设直线与轴交于 即 由直线与渐近线的交点分别在第一、四象限可知: 由(1)可得双曲线方程为: 联立与双曲线方程: 因为与双曲线相切 整理可得: 所以 双曲线方程为: 存在一个总与相切的双曲线,其方程为查看更多