【物理】2019届一轮复习人教版多维探究　殊途同归(三)　从力的角度解读传送带模型和板块模型学案

【物理】2019届一轮复习人教版多维探究　殊途同归(三)　从力的角度解读传送带模型和板块模型学案

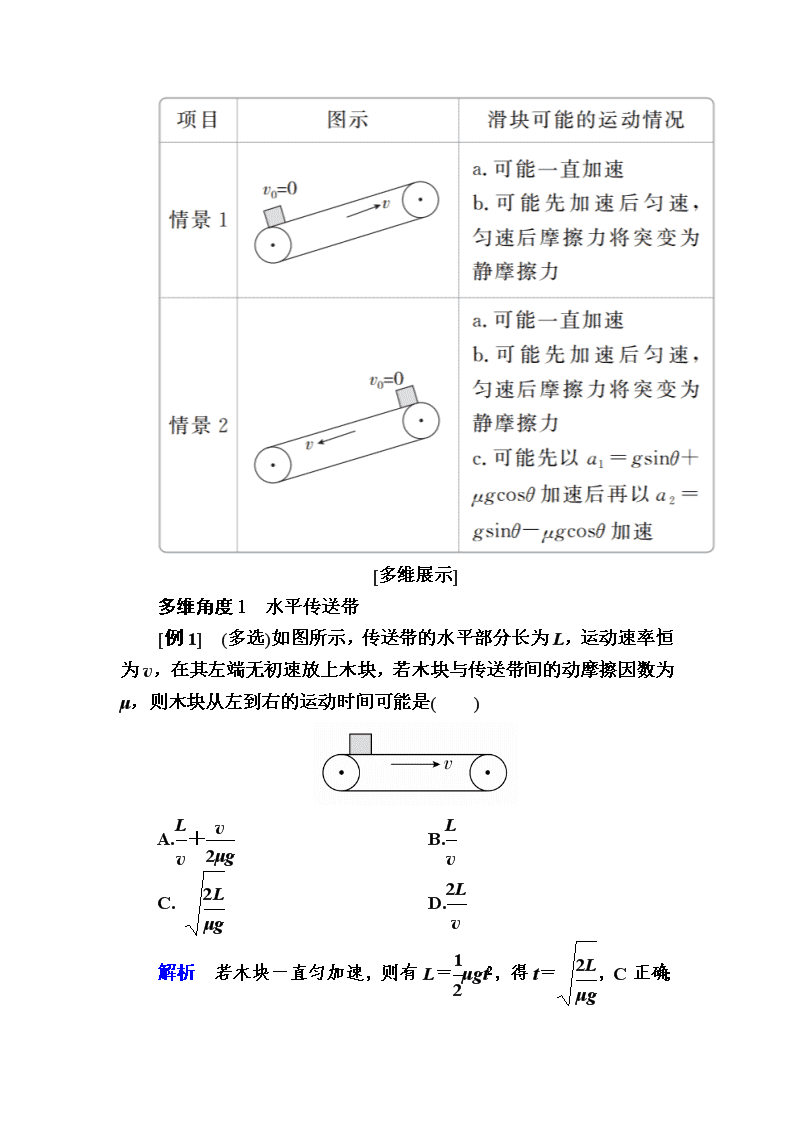
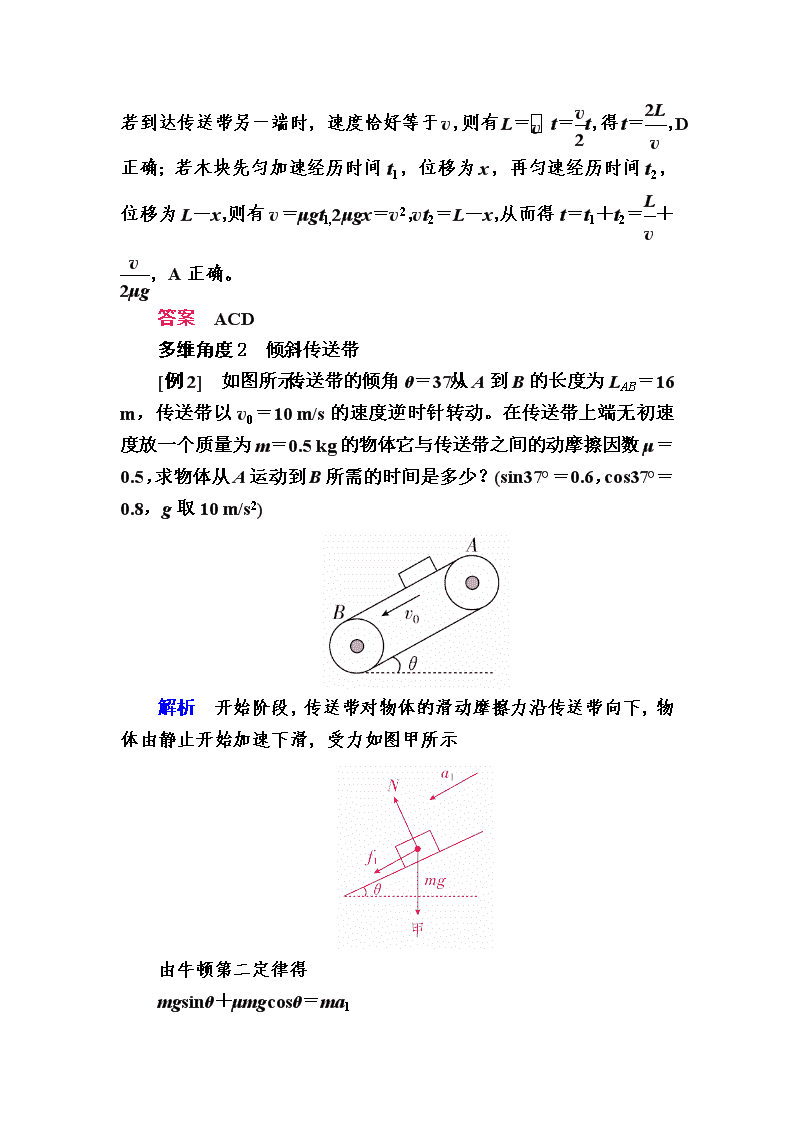
‎　从力的角度解读传送带模型 ‎[多维概述]‎ ‎1．特点：传送带始终以恒定的速率运行，物体和传送带之间μ≠0。‎ ‎2．常见传送带的模型有以下几种 ‎(1)水平传送带 ‎(2)倾斜传送带 ‎[多维展示]‎ 多维角度1 水平传送带 ‎[例1]　(多选)如图所示，传送带的水平部分长为L，运动速率恒为v，在其左端无初速放上木块，若木块与传送带间的动摩擦因数为μ，则木块从左到右的运动时间可能是(　　)‎ A.＋ B. C. D. 解析　若木块一直匀加速，则有L＝μgt2，得t＝，C正确；‎ 若到达传送带另一端时，速度恰好等于v，则有L＝ t＝t，得t＝，D正确；若木块先匀加速经历时间t1，位移为x，再匀速经历时间t2，位移为L－x，则有v＝μgt1,2μgx＝v2，vt2＝L－x，从而得t＝t1＋t2＝＋，A正确。‎ 答案　ACD 多维角度2 倾斜传送带 ‎[例2]　如图所示，传送带的倾角θ＝37°，从A到B的长度为LAB＝‎16 m，传送带以v0＝‎10 m/s的速度逆时针转动。在传送带上端无初速度放一个质量为m＝‎0.5 kg的物体，它与传送带之间的动摩擦因数μ＝0.5，求物体从A运动到B所需的时间是多少？(sin37°＝0.6，cos37°＝0.8，g取‎10 m/s2)‎ 解析　开始阶段，传送带对物体的滑动摩擦力沿传送带向下，物体由静止开始加速下滑，受力如图甲所示 由牛顿第二定律得 mgsinθ＋μmgcosθ＝ma1‎ 解得a1＝gsinθ＋μgcosθ＝‎10 m/s2‎ ‎ 物体加速至速度与传送带速度相等时需要的时间 t1＝＝1 s 物体运动的位移x1＝a1t＝‎5 m<‎‎16 m 即物体加速到‎10 m/s时仍未到达B点，当物体加速至与传送带速度相等时，由于μμ1mg＝0.3×1×10 N＝3 N 假设A、B之间不发生相对滑动，则 对A、B整体：F＝(M＋m)a 对B：fAB＝ma 解得：fAB＝2.5 N 因fABt1时，设A和B的加速度分别为a1′和a2′。此时A与B之间摩擦力为零，同理可得 a1′＝‎6 m/s2⑪‎ a2′＝－‎2 m/s2⑫‎ 即B做减速运动。‎ 设经过时间t2，B的速度减为零，则有 v2＋a2′t2＝0⑬‎ 联立⑩⑫⑬式得 t2＝1 s⑭‎ 在t1＋t2时间内，A相对于B运动的距离为 x＝－ ‎＝‎12 m<‎27 m⑮‎ 此后B静止不动，A继续在B上滑动。‎ 设再经过时间t3后A离开B，则有：‎ l－x＝(v1＋a1′t2)t3＋a1′t⑯‎ 可得 t3＝1 s(另一解不合题意，舍去)⑰‎ 设A在B上总的运动时间为t总，则有：‎ t总＝t1＋t2＋t3＝4 s。‎ 答案　(1)‎3 m/s2　‎1 m/s2　(2)4 s ‎[多途归一]‎ ‎1．特点：涉及两个物体，且物体间存在相对滑动。‎ ‎2．过程分析 ‎(1)前提一般都以地面为参考系。‎ ‎(2)存在下列几种情况：‎ ‎①同向相对运动最终不分离 ‎②同向相对运动最终分离 ‎③相向运动最终分离 ‎④相向运动最终又同向运动不分离 ‎(3)只要相对运动，需分别进行受力分析，找出各自的位移、速度和加速度的关系，找出它们的位移、速度与加速度的内在联系，再确立方程去解决。‎ ‎(4)有时速度相等是解决问题的关键，再由牛顿第二定律去分析是继续相对运动还是一起做相同的规律运动。‎ ‎[类题演练]‎ ‎1．(2017·广东模拟)(多选)如图甲所示，静止在光滑水平面上的长木板B(长木板足够长)的左端静止放着小物块A。某时刻，A受到水平向右的外力F作用，F随时间t的变化规律如图乙所示，即F＝kt，其中k为已知常数。设A、B之间的滑动摩擦力大小等于最大静摩擦力Ff，且A、B的质量相等，则下列可以定性描述长木板B运动的vt图象和物块A运动的at图象的是(　　)‎ 答案　BC 解析　A、B相对滑动之前加速度相同，由整体法可得F＝2ma，当A、B间刚好发生相对滑动时，对木板有Ff＝ma，故此时F＝2Ff＝kt，t＝之后木板做匀加速直线运动，A错误，B正确。t＝之前，A、B的共同加速度为a＝；t＝之后，对A有F－μmg＝ma，解得a＝－μg，故at图象的斜率增大，C正确，D错误。‎ ‎2. (2017·重庆八中一模)如图所示，质量M＝‎1 kg的木板静置于倾角为37°的足够长的固定斜面上的某个位置，质量m＝‎1 kg、可视为质点的小物块以初速度v0＝‎5 m/s从木板的下端冲上木板，同时在木板上端施加一个沿斜面向上的外力F＝14 N，使木板从静止开始运 动，当小物块与木板共速时，撤去该外力，最终小物块从木板的下端滑出。已知小物块与木板之间的动摩擦因数为0.25，木板与斜面之间的动摩擦因数为0.5，最大静摩擦力等于滑动摩擦力，g取‎10 m/s2，sin37°＝0.6，cos37°＝0.8.求：‎ ‎(1)物块和木板共速前，物块和木板的加速度；‎ ‎(2)木板的最小长度；‎ ‎(3)物块在木板上运动的总时间。‎ 答案　(1)见解析　(2) m　(3) s 解析　(1)物块与木板共速前，对物块分析有 mgsinθ＋μ1mgcosθ＝ma1‎ 得a1＝‎8 m/s2，方向沿斜面向下，物块减速上滑；‎ 对木板分析有 F＋μ1mgcosθ－Mgsinθ－μ2(m＋M)gcosθ＝Ma2‎ 得a2＝‎2 m/s2，方向沿斜面向上，木板加速上滑。‎ ‎(2)物块与木板共速时有v共＝v0－a1t1，v共＝a2t1‎ 代入数据解得t1＝0.5 s，v共＝‎1 m/s 共速时物块与木板的相对位移 Δx1＝v0t1－a1t－a2t＝‎1.25 m，‎ 撤掉F后，物块相对于木板上滑，加速度大小仍为a1＝‎8 m/s2，物块减速上滑，‎ 对木板有Mgsinθ＋μ2(M＋m)gcosθ－μ1mgcosθ＝Ma2′‎ 则a2′＝‎12 m/s2，方向沿斜面向下，木板减速上滑。‎ 由于Mgsinθ＋μ1mgcosθ＝μ2(M＋m)gcosθ 则木板速度减为零后，物块在木板上滑动时，木板保持静止，经过t2＝ s，木板停止，经过t2′＝ s，物块速度减为零，此过程，物块和木板的相对位移 Δx2＝t2′－t2＝ m 故木板的最小长度Lmin＝Δx1＋Δx2＝ m。‎ ‎(3)物块在木板上下滑时，木板静止不动，‎ 物块的加速度a1′＝gsinθ－μ1gcosθ＝‎4 m/s2‎ Lmin＝a1′t，得t3＝ s 物块在木板上运动的总时间 t＝t1＋t2′＋t3＝ s。‎ ‎3．(2017·全国卷Ⅲ)如图所示，两个滑块A和B的质量分别为mA＝‎1 kg和mB＝‎5 kg，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为μ1＝0.5；木板的质量为m＝‎4 kg，与地面间的动摩擦因数为μ2＝0.1。某时刻A、B两滑块开始相向滑动，初速度大小均为v0＝‎3 m/s。A、B相遇时，A与木板恰好相对静止。设最大静摩擦力等于滑动摩擦力，取重力加速度大小g＝‎10 m/s2。求：‎ ‎(1)B与木板相对静止时，木板的速度；‎ ‎(2)A、B开始运动时，两者之间的距离。‎ 答案　(1)‎1 m/s　(2)‎‎1.9 m 解析　(1)滑块A和B在木板上滑动时，木板也在地面上滑动。‎ 设A、B和木板所受的摩擦力大小分别为f1、f2和f3，A和B相对于地面的加速度大小分别是aA和aB，木板相对于地面的加速度大 小为a1。‎ 在滑块B与木板达到共同速度前有 f1＝μ1mAg①‎ f2＝μ1mBg②‎ f3＝μ2(mA＋mB＋m)g③‎ 由牛顿第二定律得 f1＝mAaA④‎ f2＝mBaB⑤‎ f2－f1－f3＝ma1⑥‎ 设在t1时刻，B与木板达到共同速度，设大小为v1。‎ 由运动学公式有 v1＝v0－aBt1⑦‎ v1＝a1t1⑧‎ 联立①②③④⑤⑥⑦⑧式，代入已知数据得 v1＝‎1 m/s⑨‎ ‎(2)在t1时间间隔内，B相对于地面移动的距离为 sB＝v0t1－aBt⑩‎ 设在B与木板达到共同速度v1后，木板的加速度大小为a2，对于B与木板组成的体系，由牛顿第二定律有 f1＋f3＝(mB＋m)a2⑪‎ 由①②④⑤式知，aA＝aB；‎ 再由⑦⑧可知，B与木板达到共同速度时，A的速度大小也为v1，但运动方向与木板相反。‎ 由题意知，A和B相遇时，A与木板的速度相同，设其大小为v2，设A的速度大小从v1变到v2所用时间为t2，则由运动学公式，对木板有v2＝v1－a2t2⑫‎ 对A有v2＝－v1＋aAt2⑬‎ 在t2时间间隔内，B(以及木板)相对地面移动的距离为s1＝v1t2－‎ a2t⑭‎ 在(t1＋t2)时间间隔内，A相对地面移动的距离为 sA＝v0(t1＋t2)－aA(t1＋t2)2⑮‎ A和B相遇时，A与木板的速度也恰好相同。‎ 因此A和B开始运动时，两者之间的距离为 s0＝sA＋s1＋sB⑯‎ 联立以上各式，并代入数据得s0＝‎1.9 m。(也可用如图的速度－时间图线求解)‎