- 2021-05-10 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教A版立体几何小题学案
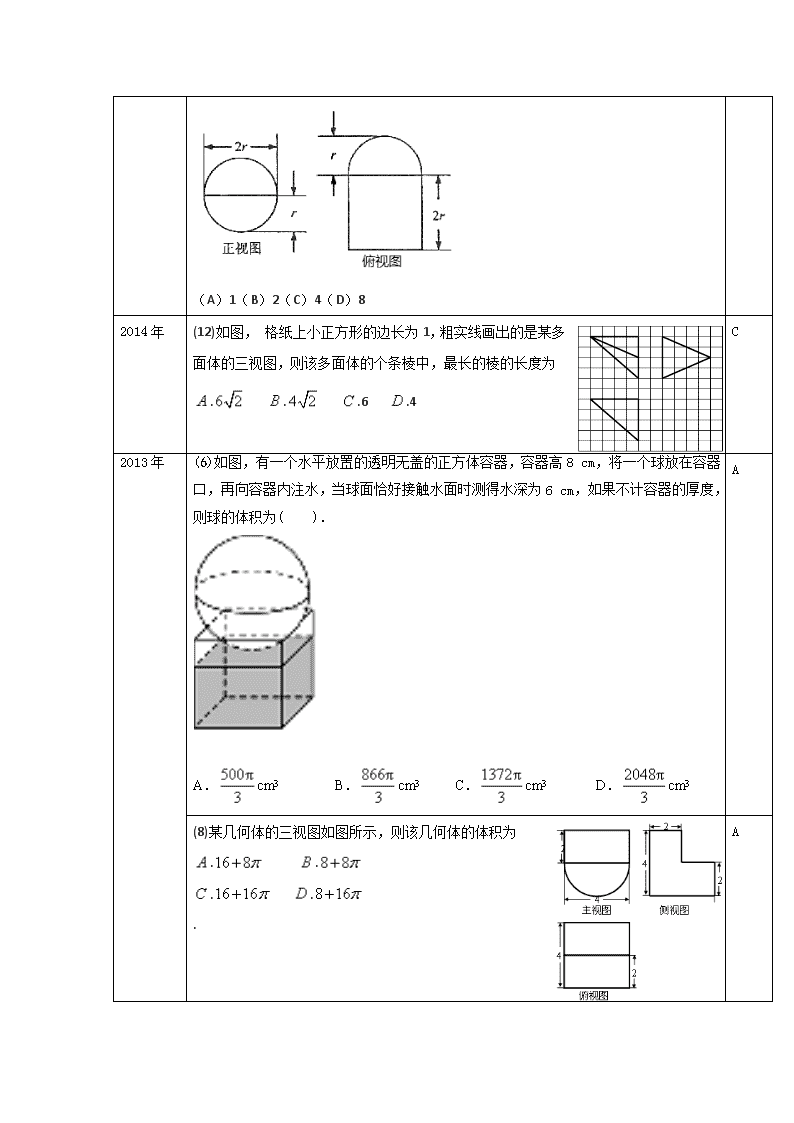
一.复数小题 (一)命题特点和预测:分析近7年的高考全国课标1试题,发现立体几何小题7年13考,每年基本上为2个小题,一个以简单几何体的三视图为载体考查简单几何体的三视图及其体积或表面积或几何体中的最值问题,一个考查简单几何体的外接球体积与表面积或空间线面、面面平行、垂直问题、空间异面直线夹角、线面角或二面角、与体积或表面积有关的最值问题等,难度既有基础题也有中档题也可为压轴题,2018年的高考仍将在保持这一考试特点的基础上会适度创新. : ] (二)历年试题比较: 年份 题目 答案 2017年 (7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为 A.10 B.12 C.14 D.16 B (16)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。 [ : 。xx。 ] 2016年 (6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是 A (A)17π(B)18π(C)20π(D)28π (11)平面过正方体ABCD-A1B1C1D1的顶点A,//平面CB1D1,平面ABCD=m,平面ABA1B1=n,则m、n所成角的正弦值为 (A) (B) (C) (D) A 2015年 (6)《九章算术》是我国古代内容极为丰富的数 名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( ) A.14斛 B.22斛 C.36斛 D.66斛 [ : , , ,X,X, ] B (11) 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示。若该几何体的表面积为16 + 20,则r= B (A)1(B)2(C)4(D)8 2014年 (12)如图, 格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为 . . .6 .4 C 2013年 (6)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( ). A.cm3 B.cm3 C.cm3 D.cm3 A (8)某几何体的三视图如图所示,则该几何体的体积为 . . . . . A 2012年 (7)如图, 格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的体积为 .6 .9 .12 .18 . B (11)已知三棱锥的所有顶点都在求的球面上,是边长为1的正三角形,为球的直径,且=2,则此三棱锥的体积为 . . . . . A 2011年 (6)在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为 D (15)已知矩形的顶点都在半径为4的球面上,且=6,,则棱锥的体积为 . 【解析与点睛】 (2017年)(7)【解析】由题知该几何体的直观图如图所示,由底面为腰长为2等腰直角三角形高为2的三棱锥与底面为该三棱柱上底面、高为2三棱锥构成,由直观图知该几何体各面只有两个是梯形且面积相等,故这些梯形面积之和为,故选B. (16)【解析】由题,连接,交与点,由题,,,即的 (2016年)(6)【解析】由三视图知,对应的几何体是球切去左前上,设球的半径为,则其体积为,解得,所以其表面积为=,故选A. (11)【解析】根据面面平行的性质定理知,直线就是,且,因为为正三角形,所以即所成的角的正弦值为,故选A. (8)【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2高为4,上边放一个长为4宽为2高为2长方体,故其体积为 =,故选. (15)【解析】设矩形的对角线的交点为E,则OE⊥面ABCD,由题知截面圆半径===12,由截面圆性质得OE==2,∴棱锥的体积为==. ! (三)命题专家押题 题号 试 题 1. 某空间几何体的三视图如下图所示,则该几何体的体积为( ) A. B. C. D. 2. 如图,已知三棱柱的正视图是边长为1的正方形,俯视图是边长为1的正三角形,点是上一动点(异于),则该三棱柱的侧视图是( ) A. B. C. D. 3 某几何体的三视图如图所示,其中正视图由矩形和等腰直角三角形组成,侧视图由半圆和等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为( ) A. B. C. D. 4 已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( ) [ : *xx* ] A. B. 4 C. 3 D. 5 已知一个几何体下面是正三棱柱,其所有棱长都为;上面是正三棱锥,它的高为,若点都在一个体积为的球面上,则的值为( ) A. B. 1 C. D. 6 如图,正方体的棱线长为,线段上有两个动点, ,且,则下列结论中正确的是__________.(写出所有正确命题的序号) () ()平面 ()三棱锥的体积为定值 ! ()的面积与的面积相等 7 四棱锥中, 平面,底面是边长为2的正方形, , 为的中点,则异面直线与所成角的余弦值为( ) A. B. C. D. [ : xx ] 8 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知“堑堵”的所有顶点都在球的球面上,且,若球的表面积为,则这个三棱柱的体积是( ) A. B. C. D. 1 9 已知、、是球的球面上三点, , , ,且棱锥的体积为,则球的表面积为( ) A. B. C. D. 10 已知三棱柱的六个顶点都在球的球面上,球的表面积为,平面,则直线与平面所成角的正弦值为( ) A. B. C. D. 【详细解析】 1.【答案】D 综上所述,结论中正确的是()()(). 7.【答案】C 【解析】如图所示,延长AD到H,使,过P作,F为PG的中点,连接BF,FH, BH,则为异面直线与所成的角或者补角,在中,由余弦定理得,故选C. 8.【答案】C ∴,∴,∴球O的表面积为: ,∴故选D. 10.【答案】C ∴, 又, ∴直线与平面所成角正弦值为.选C. 查看更多