高中数学必修2教案：圆柱、圆锥、圆台和球(3)

高中数学必修2教案：圆柱、圆锥、圆台和球(3)

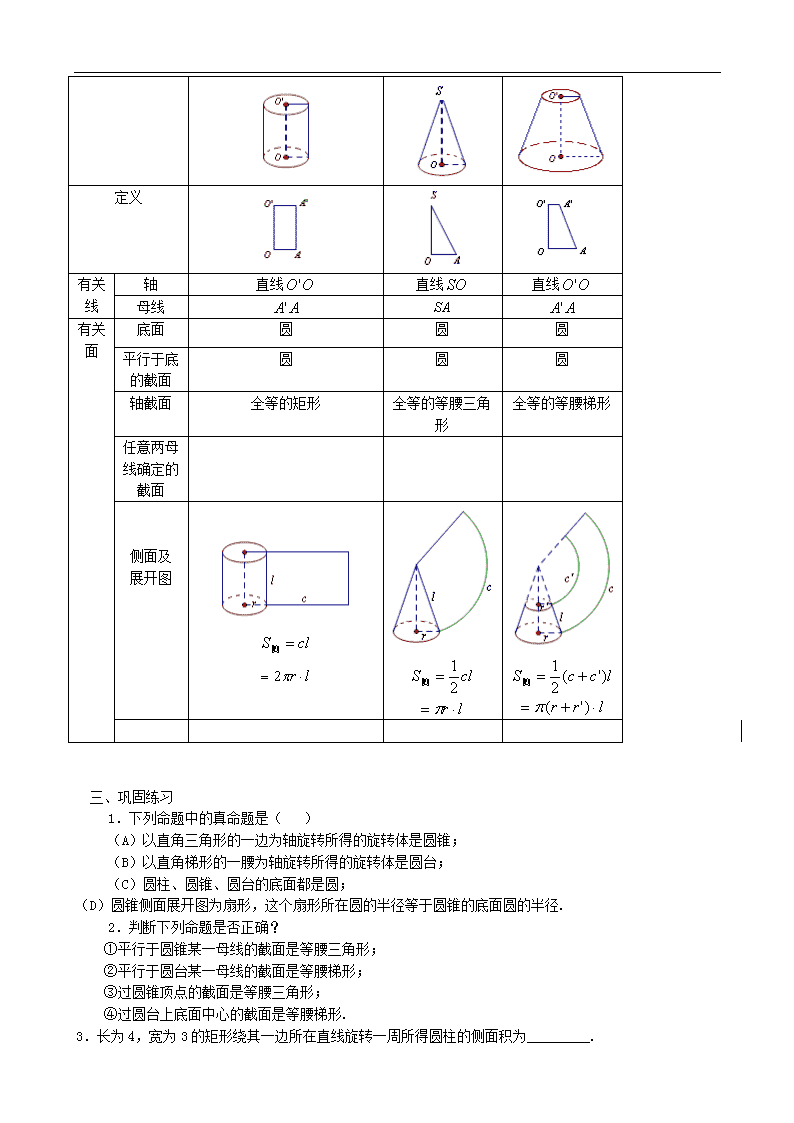
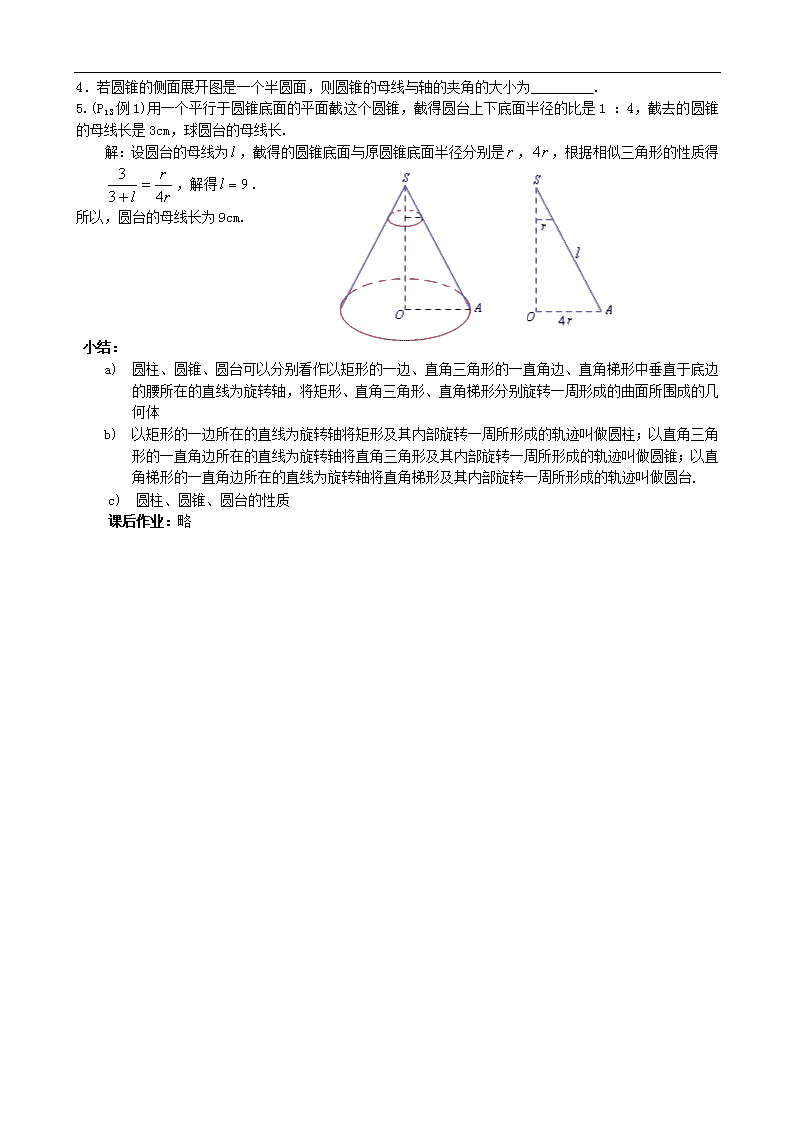
圆柱、圆锥、圆台和球(1)‎ 教学目标：1、圆柱、圆锥、圆台概念，‎ ‎2、掌握圆柱、圆锥、圆台的性质 教学重点：掌握圆柱、圆锥、圆台的性质 教学过程：‎ 一、基本概念 ‎(播放陶艺的主要制作过程.)‎ ‎(抓取实物照片)，‎ 思考：这个几何体的外部曲面是如何形成的？几何体是如何形成的？‎ ‎ 旋转面可看作一条曲线绕一条定直线旋转一周所形成的轨迹,这条定直线叫做旋转轴,简称轴.这条曲线叫做旋转面的母线.封闭的旋转面所围成的几何体叫做旋转体.旋转体也可以看作是由一封闭的平面图形包括其内部绕一条定直线旋转一周所形成的轨迹.‎ 请学生思考：圆柱、圆锥、圆台可由什么平面图形如何运动而成？‎ 定义1：(线动成面,面围成体)‎ 圆柱、圆锥、圆台可以分别看作以矩形的一边、直角三角形的一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴，将矩形、直角三角形、直角梯形分别旋转一周形成的曲面所围成的几何体.‎ 旋转轴叫做所围成的几何体的轴；在轴上的这条边的长度叫做这个几何体的高；垂直于轴的边旋转而成的圆面叫做这个几何体的底面；不垂直于轴的边旋转而成的曲面叫做这个几何体的侧面；无论旋转到什么位置，这条边都叫做侧面的母线.‎ 定义2：(面动成体)‎ 以矩形的一边所在的直线为旋转轴将矩形及其内部旋转一周所形成的轨迹叫做圆柱；以直角三角形的一直角边所在的直线为旋转轴将直角三角形及其内部旋转一周所形成的轨迹叫做圆锥；以直角梯形的一直角边所在的直线为旋转轴将直角梯形及其内部旋转一周所形成的轨迹叫做圆台.‎ 圆柱、圆锥、圆台之间有何关系？（教师演示，学生观察总结）‎ ‎①平行于底面截圆锥可以得到圆台；‎ 用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分叫做圆台.‎ ‎②圆台的上底变大可以得到圆柱；‎ ‎③圆台的上底变小可以得到圆锥.‎ 让学生举出一些圆柱、圆锥、圆台的实例，以及其他旋转体的实例.‎ 让学生思考：如图，一个半圆面绕其直径所在直线旋转一周所形成的几何体是什么？一个圆面绕一条直线旋转一周形成的几何体是什么？‎ ‎ ‎ 二、主要性质 定义 有关线 轴 直线 直线 直线 母线 有关面 底面 圆 圆 圆 平行于底 的截面 圆 圆 圆 轴截面 全等的矩形 全等的等腰三角形 全等的等腰梯形 任意两母线确定的截面 侧面及 展开图 三、巩固练习 ‎1．下列命题中的真命题是（ ）‎ ‎（A）以直角三角形的一边为轴旋转所得的旋转体是圆锥；‎ ‎（B）以直角梯形的一腰为轴旋转所得的旋转体是圆台；‎ ‎（C）圆柱、圆锥、圆台的底面都是圆；‎ ‎（D）圆锥侧面展开图为扇形，这个扇形所在圆的半径等于圆锥的底面圆的半径.‎ ‎2．判断下列命题是否正确？‎ ‎①平行于圆锥某一母线的截面是等腰三角形；‎ ‎②平行于圆台某一母线的截面是等腰梯形；‎ ‎③过圆锥顶点的截面是等腰三角形；‎ ‎④过圆台上底面中心的截面是等腰梯形.‎ ‎3．长为4，宽为3的矩形绕其一边所在直线旋转一周所得圆柱的侧面积为_________.‎ ‎4．若圆锥的侧面展开图是一个半圆面，则圆锥的母线与轴的夹角的大小为_________.‎ ‎5.(P13例1)用一个平行于圆锥底面的平面截这个圆锥，截得圆台上下底面半径的比是1 ：4，截去的圆锥的母线长是3cm，球圆台的母线长.‎ 解：设圆台的母线为，截得的圆锥底面与原圆锥底面半径分别是，，根据相似三角形的性质得 ‎，解得.‎ 所以，圆台的母线长为9cm.‎ ‎ 小结：‎ a) 圆柱、圆锥、圆台可以分别看作以矩形的一边、直角三角形的一直角边、直角梯形中垂直于底边的腰所在的直线为旋转轴，将矩形、直角三角形、直角梯形分别旋转一周形成的曲面所围成的几何体 b) 以矩形的一边所在的直线为旋转轴将矩形及其内部旋转一周所形成的轨迹叫做圆柱；以直角三角形的一直角边所在的直线为旋转轴将直角三角形及其内部旋转一周所形成的轨迹叫做圆锥；以直角梯形的一直角边所在的直线为旋转轴将直角梯形及其内部旋转一周所形成的轨迹叫做圆台.‎ c) 圆柱、圆锥、圆台的性质 课后作业：略