2021版高考数学一轮复习核心素养测评二十九平面向量的数量积及平面向量的应用理北师大版
核心素养测评二十九 平面向量的数量积及平面向量的应用
(30分钟 60分)
一、选择题(每小题5分,共25分)
1.已知向量a=(1,-1),b=(2,x),若a·b=1,则x= ( )
A.-1 B.- C. D.1
【解析】选D.a·b=1×2+(-1)×x=2-x=1,所以x=1.
2.(2020·十堰模拟)若夹角为θ的向量a与b满足|b|=|a-b|=1,且向量a为非零向量,则|a|= ( )
A.-2cos θ B.2cos θ
C.-cos θ D.cos θ
【解析】选B.因为|b|=|a-b|=1,所以b2=a2-2a·b+b2,a2=2a·b,|a|2=2|a||b|cos θ,因为a为非零向量,所以|a|=2|b|cos θ=2cos θ.
3.(2020·铜川模拟)已知平面向量a=(-2,3),b=(1,2),向量λa+b与b垂直,则实数λ的值为 ( )
A. B.- C. D.-
【解析】选D.因为a=(-2,3),b=(1,2),
所以λa+b=(-2λ+1,3λ+2).
因为λa+b与b垂直,所以(λa+b)·b=0,
所以(-2λ+1,3λ+2)·(1,2)=0,
即-2λ+1+6λ+4=0,解得λ=-.
4.(2019·广州模拟)已知非零向量a,b的夹角为60°,|a|=2,|a-2b|=2,则|b|等于 ( )
A.4 B.2 C. D.1
【解析】选D.因为|a-2b|=2,所以|a-2b|2=4,
a2-4a·b+4b2=4,4-4·2|b|cos 60°+4|b|2=4,
解得|b|=1.(|b|=0舍去)
5.已知|a|=6,|b|=3,向量a在b方向上的投影是4,则a·b为 ( )
- 10 -
A.12 B.8 C.-8 D.2
【解析】选A.因为|a|cos
=4,|b|=3,所以a·b=|a||b|·cos=12.
二、填空题(每小题5分,共15分)
6.(2020·太原模拟)如图所示,在等腰直角三角形AOB中,OA=OB=1,=4,则·(-)=________________.
【解析】由已知得||=,||=,
则·(-)=(+)·=·+·=cos+×=-.
答案:-
7.已知向量m与n满足|m|=1,|n|=2,且m⊥(m+n),则向量m与n的夹角为________________.
【解析】设m,n的夹角为θ,因为m⊥(m+n),所以m·(m+n)=m2+m·n=1+1×
2cos θ=0,所以cos θ=-,又θ∈,所以θ=.
答案:
【变式备选】
已知向量a,b满足|a|=|b|=2且(a+2b)·(a-b)=-2,则向量a与b的夹角为________________.
【解析】设a与b的夹角为θ.由已知a2-2b2+a·b=-2,4-8+4cos θ=-2,cos θ=,又θ∈[0,π],所以θ=,即a与b的夹角为.
答案:
8.已知正方形ABCD的边长为2,E为CD的中点,则·=________________.
- 10 -
【解析】在边长为2的正方形ABCD中,·=0,因为·=(+)·(+)=·(-)=+·-·-=4+0-0-×4=2.
答案:2
【变式备选】
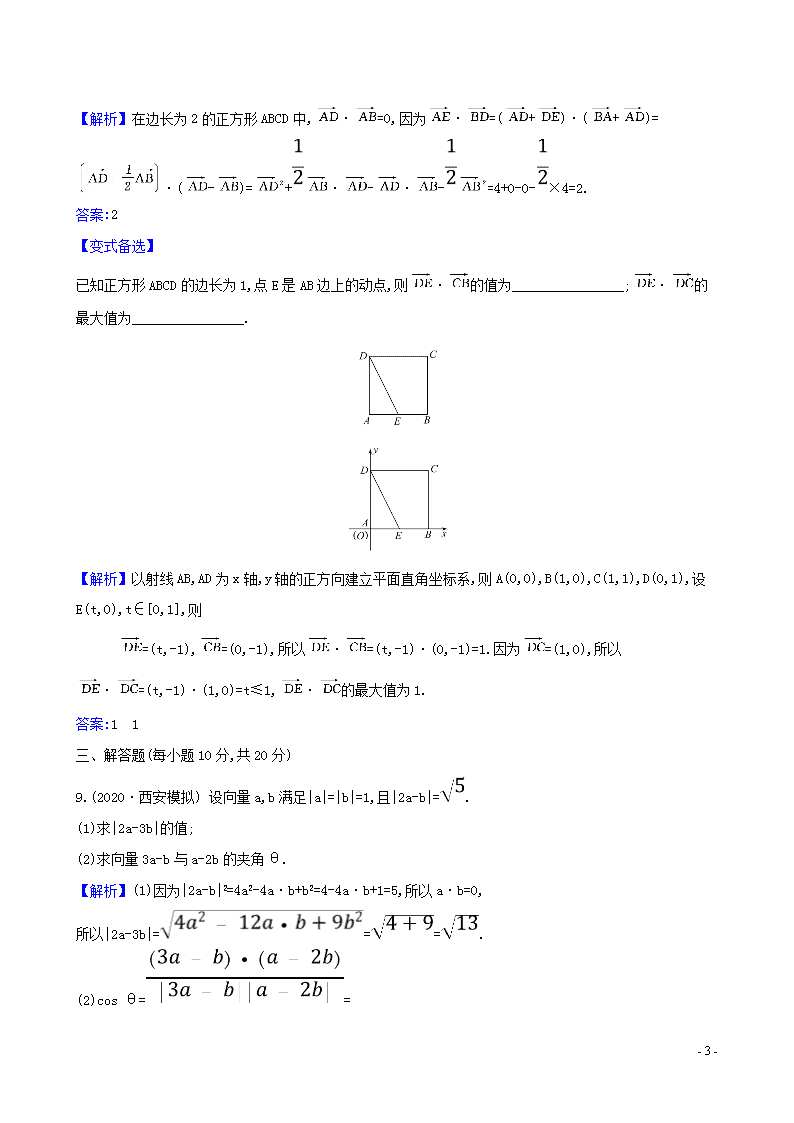
已知正方形ABCD的边长为1,点E是AB边上的动点,则·的值为________________;·的最大值为________________.
【解析】以射线AB,AD为x轴,y轴的正方向建立平面直角坐标系,则A(0,0),B(1,0),C(1,1),D(0,1),设E(t,0),t∈[0,1],则
=(t,-1),=(0,-1),所以·=(t,-1)·(0,-1)=1.因为=(1,0),所以·=(t,-1)·(1,0)=t≤1,·的最大值为1.
答案:1 1
三、解答题(每小题10分,共20分)
9.(2020·西安模拟) 设向量a,b满足|a|=|b|=1,且|2a-b|=.
(1)求|2a-3b|的值;
(2)求向量3a-b与a-2b的夹角θ.
【解析】(1)因为|2a-b|2=4a2-4a·b+b2=4-4a·b+1=5,所以a·b=0,
所以|2a-3b|===.
(2)cos θ==
- 10 -
==,
因为θ∈[0,π],所以θ=.
10.在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
(1)求以线段AB,AC为邻边的平行四边形两条对角线的长.
(2)设实数t满足(-t)·=0,求t的值.
【解析】(1)由已知=(3,5),=(-1,1),则
+=(2,6),-=(4,4).
所以|+|=2,|-|=4.
所以所求的两条对角线的长分别为4,2.
(2)由已知,=(-2,-1),
-t=(3+2t,5+t).由(-t)·=0得
(3+2t,5+t)·(-2,-1)=0,所以5t=-11,
所以t=-.
(15分钟 35分)
1.(5分)(2020·潮州模拟)已知向量a、b为单位向量,且a+b在a的方向上的投影为+1,则向量a与b的夹角为 ( )
A. B. C. D.
- 10 -
【解析】选A.设向量a与b的夹角为θ,因为向量a、b为单位向量,a+b在a的方向上的投影为+1,所以(a+b)·a=|a|,变形得1+a·b=+1,即a·b=1×1×cos θ=cos θ=,又由0≤θ≤π,则θ=,故选A.
2.(5分)(2020·大同模拟) 已知i,j为互相垂直的单位向量,a=i-2j,b=i+λj,且a与b的夹角为锐角,则实数λ的取值范围是 ( )
A.∪
B.
C.(-∞,-2)∪
D.
【解析】选C.不妨令i=(1,0),j=(0,1),则a=(1,-2),b=(1,λ),因为它们的夹角为锐角,所以a·b=1-2λ>0且a,b不共线,所以λ<且λ≠-2,故选C.
3.(5分)在Rt△ABC中,∠B=90°,BC=2,AB=1,D为BC的中点,E在斜边AC上,若=2,则·=____________.
【解析】如图,以B为原点,AB所在直线为x轴,BC所在直线为y轴,建立平面直角坐标系,则B(0,0),A(1,0),C(0,2),=(-1,2).
- 10 -
因为D为BC的中点,所以D(0,1),因为=2,所以E,=,所以·=·(-1,2)=-+=.
答案:
4.(10分)(2020·郑州模拟)已知向量m=(2sin ωx,cos2ωx-sin2ωx),n=(cos ωx,1),其中ω>0,x∈R.若函数f(x)=m·n的最小正周期为π.
(1)求ω的值.
(2)在△ABC中,若f(B)=-2,BC=,sin B=sin A,求·的值.
【解析】(1)f(x)=m·n=2sin ωxcos ωx+cos2ωx-sin2ωx=sin 2ωx+
cos 2ωx=2sin.
因为f(x)的最小正周期为π,
所以T==π,又ω>0,所以ω=1.
(2)由(1)知f(x)=2sin.
设△ABC中角A,B,C所对边分别是a,b,c.
因为f(B)=-2,所以2sin=-2,
- 10 -
即sin=-1,又0
查看更多