山东省聊城市高唐县2018-2019学年八年级上学期期末考试数学试题

山东省聊城市高唐县2018-2019学年八年级上学期期末考试数学试题

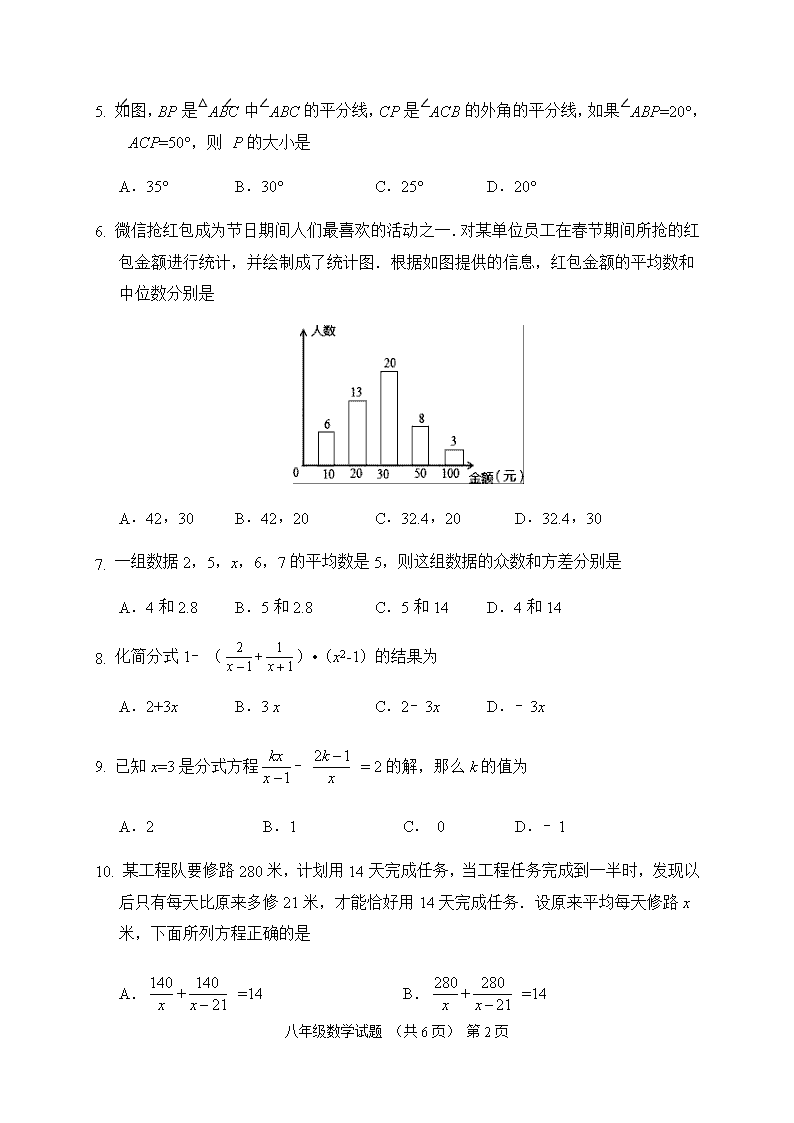
‎2018—2019学年度第一学期期末学业水平检测 八年级数学试题 第Ⅰ卷（选择题 共36分）‎ 一、 选择题（每题3分，共36分）‎ 1. 计算（﹣a）2 • 的结果为 A．b 　　　　 B．﹣b 　　　　C．ab 　 D．‎ ‎2. 下列命题是真命题的是 ‎ A．同旁内角互补 B．三角形的一个外角等于它的两个内角之和 C．直角三角形的两个锐角互余 D．三角形的一个外角大于任意一个内角 ‎3. 如图，AB=DB，∠1=∠2，请问添加下面哪个条件不能判断△ABC≌△DBE的是 A．BC=BE B．AC=DE C．∠A=∠D D．∠ACB=∠DEB ‎ ‎ 第3题图 第4题图 第5题图 ‎ 4. 如图，在△ABC中，AB=AC，若以点B为圆心，BC长为半径作弧，交AC于点E，则下列结论一定正确的是 ‎ ‎ A.AE=BE B. BE是∠ABC的角平分线 C.∠A=∠EBC D. AE=BC 八年级数学试题 （共6页） 第12页 ‎5. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠P的大小是 ‎ A．35° B．30° C．25° D．20°‎ ‎6. 微信抢红包成为节日期间人们最喜欢的活动之一．对某单位员工在春节期间所抢的红包金额进行统计，并绘制成了统计图．根据如图提供的信息，红包金额的平均数和中位数分别是 ‎ A．42，30 B．42，20 C．32.4，20 D．32.4，30‎ 7. 一组数据2，5，x，6，7的平均数是5，则这组数据的众数和方差分别是 ‎ A．4和2.8 B．5和2.8 C．5和14 D．4和14‎ 8. 化简分式1﹣（）•（x2-1）的结果为 A．2+3x B．3 x C．2﹣3x D．﹣3x ‎9. 已知x=3是分式方程﹣ = 2的解，那么k的值为 ‎ A．2 B．1 C． 0 D．﹣1‎ ‎10. 某工程队要修路280米，计划用14天完成任务，当工程任务完成到一半时，发现以后只有每天比原来多修21米，才能恰好用14天完成任务．设原来平均每天修路x米，下面所列方程正确的是 ‎ A． =14 B． =14‎ 八年级数学试题 （共6页） 第12页 C． =14 D． =14‎ ‎11. 如图，四边形ABCD中，AB=AD，AC=5，∠DAB=∠DCB=90°，则四边形ABCD的面积为 A．12.5 　　 B．14.5　　　 C．15 　　 D．17‎ ‎ ‎ 第11题图 第12题图 12. 如图，△ABE、△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3=7：2：1，则∠α的度数为 ‎ A.90° B.108° C.110° D.126°‎ 第Ⅱ卷（非选择题 共84分）‎ 二、填空题（每题3分，共15分）‎ ‎13. 如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有　 　个．‎ ‎14. 如图，在△ABC中，∠ACB=68°，若P为△ABC内一点，且∠1=∠2，则∠BPC=_______．‎ ‎15. 如果a=b+4，那么代数式的值为　 　. ‎ ‎ ‎ 八年级数学试题 （共6页） 第12页 第13题图 第14题图 第16题图 第17题图 ‎16．如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于，且OD=4，△ABC的面积是　 　．‎ ‎17. 如图，把平面内一条数轴x绕原点O逆时针旋转角θ（0°＜θ＜90°）得到另一条数轴y，x轴和y轴构成一个平面斜坐标系．规定：过点P作y轴的平行线，交x轴于点A，过点P作x轴的平行线，交y轴于点B，若点A在x轴上对应的实数为a，点B在y轴上对应的实数为b，则称有序实数对（a，b）为点P的斜坐标，在某平面斜坐标系中，已知θ=60°，点M的斜坐标为（2，3），点N与点M关于y轴对称，则点N的斜坐标为　 　．（温馨提示：直角三角形中30°所对的直角边等于斜边的一半.）‎ 三、解答题（本题共8个小题，共计69分.解答题应写出文字说明、证明过程或推理步骤）‎ ‎18.（本题满分8分，每小题4分）解下列分式方程 ‎（1） （2）‎ ‎19.（本题满分8分，（1）题3分，（2）题5分）‎ ‎（1）化简： ‎ ‎（2）先化简，再求值：，其中.‎ ‎20.（本题满分7分）近年来，随着我国的科学技术的迅猛发展，很多行业已经由“中国制造”升级为“中国创造”，高铁事业是“中国创造”的典范，一般的高铁包括G字头的高速动车组以及D字头的动车组．由大连到北京的G377的平均速度是D31的平均速度的1.2倍，行驶相同的路程1500千米，G377少用1个小时．‎ ‎（1）求D31的平均速度．‎ 八年级数学试题 （共6页） 第12页 ‎（2）若以“速度与票价的比值”定义这两种列车的性价比，人们出行都喜欢选择性价比高的方式．现阶段D31票价为266元/张，G377票价为400元/张，如果你有机会给有关部门提一个合理化建议，使G377的性价比达到D31的性价比，你如何建议，为什么？‎ ‎21.（本题满分8分）如图，在平面直角坐标系中，每个小正方形边长为1，点A的坐标为(－2，3)、点B的坐标为(－3，1)、点C的坐标为(1，-2) ．‎ ‎（1）作出△ABC关于y轴对称的△A′B′C′,‎ ‎（其中A′、B′、C′分别是A、B、C的对应点，不写画法） ； ‎ ‎（2）直接写出A′、B′、C′三点的坐标；‎ ‎（3）在x轴上求作一点P，使PA+PB的值最小．（简要写出作图步骤）‎ ‎22.（本题满分8分）如图，△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB，延长AC至E，使CE=AC．‎ ‎（1）求证：DE=DB；‎ ‎（2）连接BE，试判断△ABE的形状，并说明理由．‎ ‎23.（本题满分8分）时代中学为选拔一名选手参加“不忘初心，永远跟党走”主题演讲比赛，经研究，按图所示的项目和权数对选拔赛参赛选手进行考评（因排版原因统计图不完整）．下表是小亮、小颖在选拔赛中的得分情况：‎ 八年级数学试题 （共6页） 第12页 ‎ 项目 选手[来源:学#科#网]‎ 服装 普通话 主题 演讲 技巧 小亮 ‎85‎ ‎70‎ ‎80‎ ‎85‎ 小颖 ‎90‎ ‎75‎ ‎75‎ ‎80‎ ‎ ‎ 结合以上信息，回答下列问题：‎ ‎（1）求服装项目的权；‎ ‎（2）求小亮在选拔赛中四个项目所得分数的众数和中位数；‎ ‎（3）根据你所学的知识，帮助学校在小亮、小颖两人中选择一人参加“不忘初心，永远跟党走”主题演讲比赛，并说明理由．‎ ‎24.（本题满分10分）已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点．‎ ‎（1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；‎ ‎（2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE与AF满足什么样的数量关系？请利用图②说明理由．‎ 八年级数学试题 （共6页） 第12页 ‎25.（本题满分12分）如图，AB⊥BC，射线CM⊥BC，且BC=7cm，AB=2cm，点P是线段BC（不与点B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连结AD．‎ ‎（1）如图1，若BP=5cm，求证：△ABP≌△PCD；‎ ‎（2）如图2，若DP平分∠ADC，试猜测PB和PC的数量关系，并说明理由；‎ ‎（3）若△PDC是等腰三角形，求CD的长．‎ 八年级数学试题 （共6页） 第12页 ‎2018—2019学年度第一学期期末学业水平检测 八年级数学参考答案 一、 选择题 (每小题3分，共36分。每小题只有一个选项符合题意)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 选项 A C B C B D B D A D A B 二、 填空题（每小题3分，共15分。每小题只填写最后结果）‎ ‎13. 5个 14. 112° 15. 2 16. 42 17. （﹣2，5） ‎ 三、 解答题(共7小题，共69分。解答应写出必要的步骤)‎ ‎18.（本题满分8分，每小题4分）‎ 解：（1）去分母得：x2﹣x=x2﹣2x﹣3，解得：x=﹣3， ……………………3分 经检验x=﹣3是原方程的根；…………………………………………………4分 ‎（2）去分母得：x2+4x﹣x2﹣2x+8=12，解得：x=2，………………………………3分 经检验x=2是增根，分式方程无解． …………………………………………4分 ‎ 19.（本题满分8分，（1）题3分，（2）题5分）‎ ‎（1）原式= • = ﹣• = ……………………3分 ‎（2）原式=﹣m-2‎m+2‎ =‎2-m‎2+m…………………………………………………………3分 ‎ 当m=﹣ 时，原式=………………………………………………………5分 ‎20.（本题满分7分）‎ 解：（1）设D31的平均速度为x千米/时，则G377的平均速度为1.2x千米/时．由题意：﹣=1，……………………………………………………3分 八年级数学试题 （共6页） 第12页 解得x=250． ‎ 经检验：x=250，是分式方程的解，且符合题意．………………………4分 所以，D31的平均速度250千米/时．……………………………………5分 ‎（2）G377的性价比==0.75 D31的性价比==0.94，…………7分 ‎∵0.94＞0.75 ∴为了G377的性价比达到D31的性价比，建议降低G377票价． ……………………………………………………………………………8分 ‎21.（本题满分8分）（1）如图所示△A′B′C′……………………………………………3分 ‎ （2）A′(2，3)、B′(3，1)、C′(－1，2) ……………………………………………6分 ‎（3）如图所示P点即为所求找到点B关于x轴的对称点B′′,连接AB′′交x轴于点P,此时PA+PB的值最小.………………………………………………………8分 ‎22.（本题满分8分）（1）证明：∵∠ACB=90°，∠ABC=30°，∴BC⊥AE，∠CAB=60°， ‎ ‎∵AD平分∠CAB，∴∠DAB=∠CAB=30°=∠ABC，∴DA=DB，‎ ‎∵CE=AC，∴BC是线段AE的垂直平分线，∴DE=DA，‎ ‎∴DE=DB； …………………4分 ‎（2）△ABE是等边三角形；理由如下：连接BE，如图：‎ ‎∵BC是线段AE的垂直平分线，∴BA=BE，‎ 即△ABE是等腰三角形，又∵∠CAB=60°，‎ ‎∴△ABE是等边三角形．……………………8分 ‎23.（本题满分8分）‎ 解：（1）服装项目的权是：1﹣20%﹣30%﹣40%=10%；……………………………2分 ‎（2）小亮在选拔赛中四个项目所得分数的众数是85，…………………………3分 中位数是：（80+85）÷2=82.5；…………………………………………………4分 八年级数学试题 （共6页） 第12页 ‎（3）小亮得分为：85×10%+70×20%+80×30%+85×40%=80.5，‎ 小颖得分为：90×10%+75×20%+75×30%+80×40%=78.5， ……………………6分 ‎∵80.5＞78.5，∴小亮的演讲成绩好，‎ 故选择小亮参加“不忘初心，永远跟党走”主题演讲比赛．……………………8分 ‎24.（本题满分10分）（1）证明：连接AD，如图①所示．‎ ‎∵∠A=90°，AB=AC，‎ ‎∴△ABC为等腰直角三角形，∠EBD=45°．‎ ‎∵点D为BC的中点，‎ ‎∴AD=BC=BD，∠FAD=45°．‎ ‎∵∠BDE+∠EDA=90°，∠EDA+∠ADF=90°，‎ ‎∴∠BDE=∠ADF． ………………………………………………………3分 在△BDE和△ADF中，，‎ ‎∴△BDE≌△ADF（ASA），‎ ‎∴BE=AF； ……………………………………………………………………………5分 ‎（2）BE=AF，证明如下：‎ 连接AD，如图②所示．‎ ‎∵∠ABD=∠BAD=45°，‎ ‎∴∠EBD=∠FAD=135°．‎ ‎∵∠EDB+∠BDF=90°，∠BDF+∠FDA=90°，‎ ‎∴∠EDB=∠FDA．……………………………………………………………………8分 在△EDB和△FDA中，，‎ 八年级数学试题 （共6页） 第12页 ‎∴△EDB≌△FDA（ASA），‎ ‎∴BE=AF．……………………………………………………………………………10分 ‎　　　‎ ‎25.（本题满分12分）‎ 解：（1）∵DP⊥AP，∴∠APD=90°，∴∠APB+∠CPD=90°，‎ ‎∵BC=7cm，BP=5cm，∴PC=2cm，∴AB=PC，‎ ‎∵∠APB+∠CPD=90°，∠APB+∠BAP=90°，∴∠BAP=∠CPD，‎ 在△ABP和△PCD中，，∴△ABP≌△PCD（AAS）；………3分 ‎（2）PB=PC，‎ 理由：如图2，延长线段AP、DC交于点E，∵DP平分∠ADC，∴∠ADP=∠EDP．‎ ‎∵DP⊥AP，∴∠DPA=∠DPE=90°，‎ 在△DPA和△DPE中，，∴△DPA≌△DPE（ASA），∴PA=PE．‎ ‎∵AB⊥BP，CM⊥CP，∴∠ABP=∠ECP=90°．‎ 在△APB和△EPC中，，‎ ‎∴△APB≌△EPC（AAS），∴PB=PC；…………………8分 ‎（3）∵△PDC是等腰三角形，‎ ‎∴△PCD为等腰直角三角形，即∠DPC=45°，‎ 又∵DP⊥AP，∴∠APB=45°，∴BP=AB=2cm，‎ 八年级数学试题 （共6页） 第12页 ‎∴PC=BC﹣BP=5cm，∴CD=CP=5cm. ………………………………12分 八年级数学试题 （共6页） 第12页