高中数学选修2-1课件常用逻辑用语复习小结

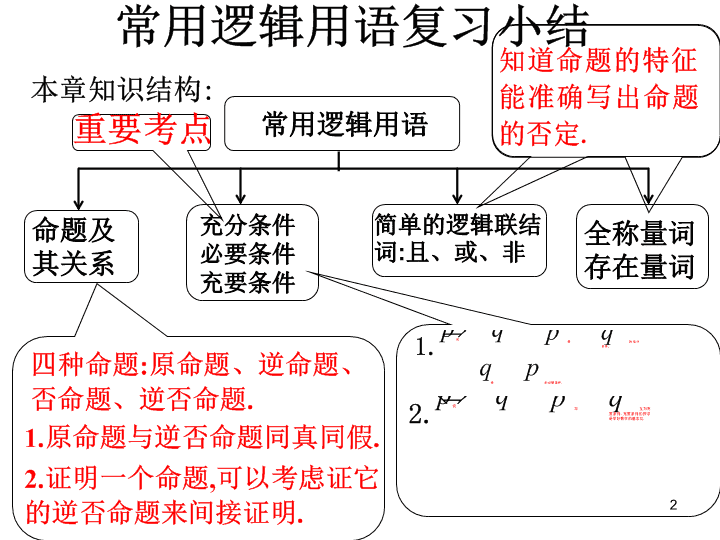
高中数学选修2-1课件常用逻辑用语复习小结

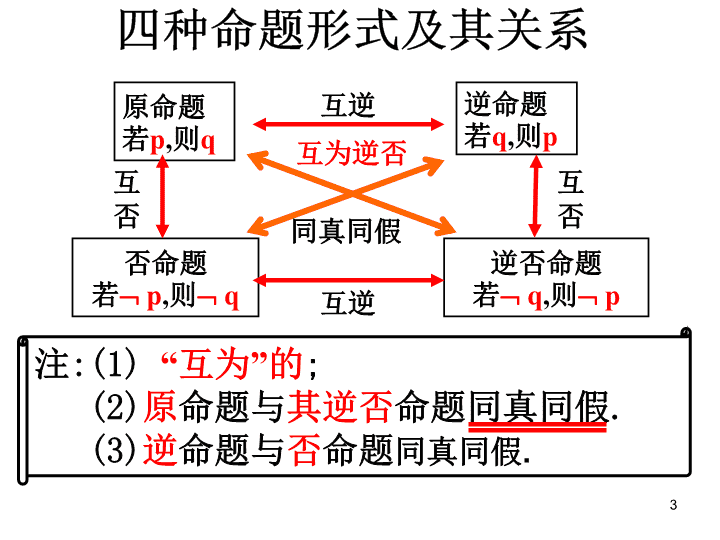
1 2 常用逻辑用语 命题及其关系 全称量词存在量词 充分条件必要条件充要条件 简单的逻辑联结词 : 且、或、非 3 注 :(1) “ 互为 ” 的 ; (2) 原 命题与 其逆否 命题同真同假 . (3) 逆 命题与 否 命题 同真同假 . 原命题 若 p , 则 q 逆否命题 若  q , 则  p 否命题 若  p , 则  q 逆命题 若 q , 则 p 互逆 互 否 互 否 互逆 互为逆否 同真同假 4 二、充要条件、必要条件的判定 对于充分条件和必要条件，要能够正确地理解和判断 (2) 从命题的角度去理解． 设原命题为 “ 若 p ，则 q ” ，则 ①若原命题为真，则 p 是 q 的 ． ②若逆命题为真，则 p 是 q 的 ． ③若原命题和逆命题都为真，则 p 是 q 的 . ④ 若原命题为真而逆命题为假，则 p 是 q 的 . ⑤ 若原命题为假而逆命题为真，则 p 是 q 的 ． ⑥若原命题和逆命题都为假，则 p 是 q 的 . 充分条件 必要条件 充要条件 充分不必要条件 必要不充分件 既不充分也不必要条件 (1) 从概念的角度去理解． ①若 p  q ，则称 p 是 q 的充分条件， q 是 p 的必要条件． ②若 p  q ，则 p 是 q 的充要条件． ⑧若 p  q ，且 qp ，则称 p 是 q 的充分不必要条件． ④若 pq ，且 q  p ，则称 p 是 q 的必要不充分条件． ⑤若 pq ，且 qp ，则称 p 是 q 的既不充分也不必要条件     5 (3) 从集合的角度去理解． 若 p 以集合 A 的形式出现， q 以集合 B 的形式出现，即 A={x|p(x)} ， B={x|q(x)) ，则 ①若 A  B ，则 p 是 q 的 ． ②若 B  A ，则 p 是 q 的 ． ③若 A=B ，则 p 是 q 的 ． ④若 A  B 且 B  A ，则 p 是 q 的 ． ⑤若 B  A 且 A  B ，则 p 是 q 的 ． ⑥若 A  B 且 B  A ，则 p 是 q 的 . 充分条件 必要条件 充要条件 充分不必要条件 必要不充分条件 既不充分也不必要条件     6 同步练习 1. A 2. C 3. B 7 4. 设 p ：实数 x 满足 x 2 -4ax+3a 2 <0 ，其中 a<0 ； q ：实数 x 满足 x 2 -x-6≤0 或 x 2 +2x-8>0 ，且 ¬ P 是 ¬ q 的必要不充分条件， 求 a 的取值范围． 也就是 p  q 且 qp ． 化简条件 p 得， A={x|3a

查看更多