- 2021-05-09 发布 |
- 37.5 KB |
- 4页

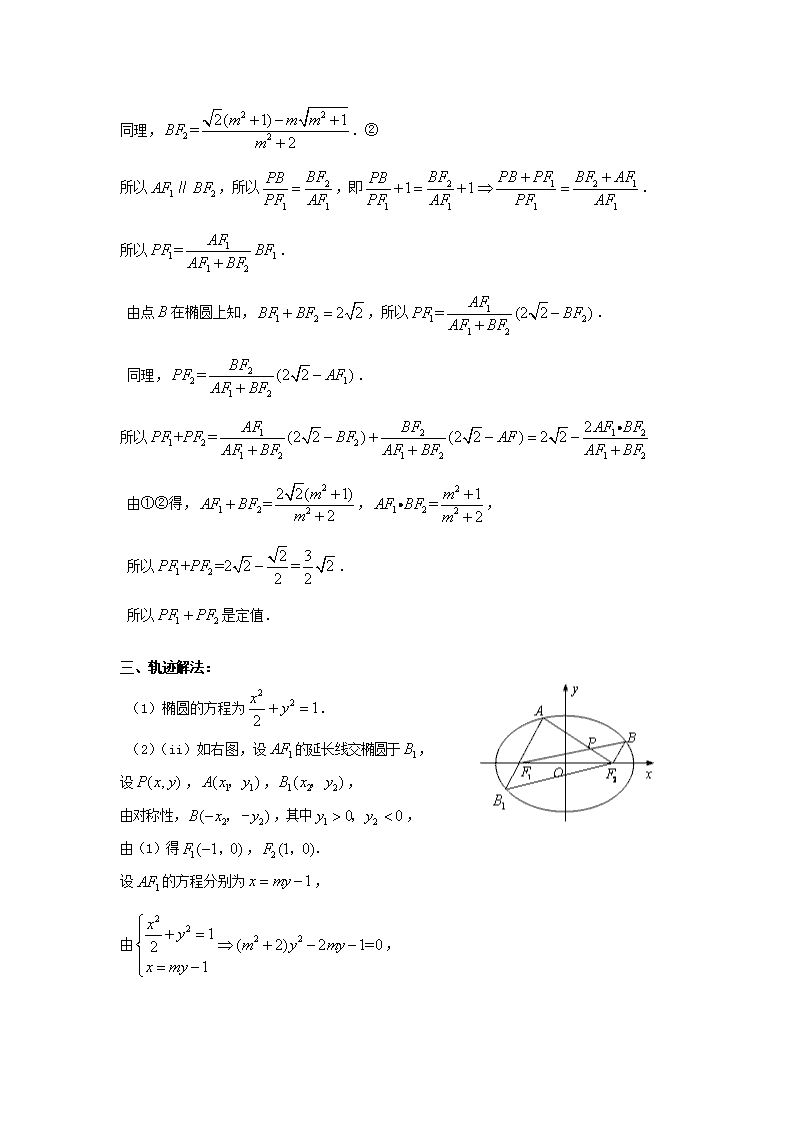
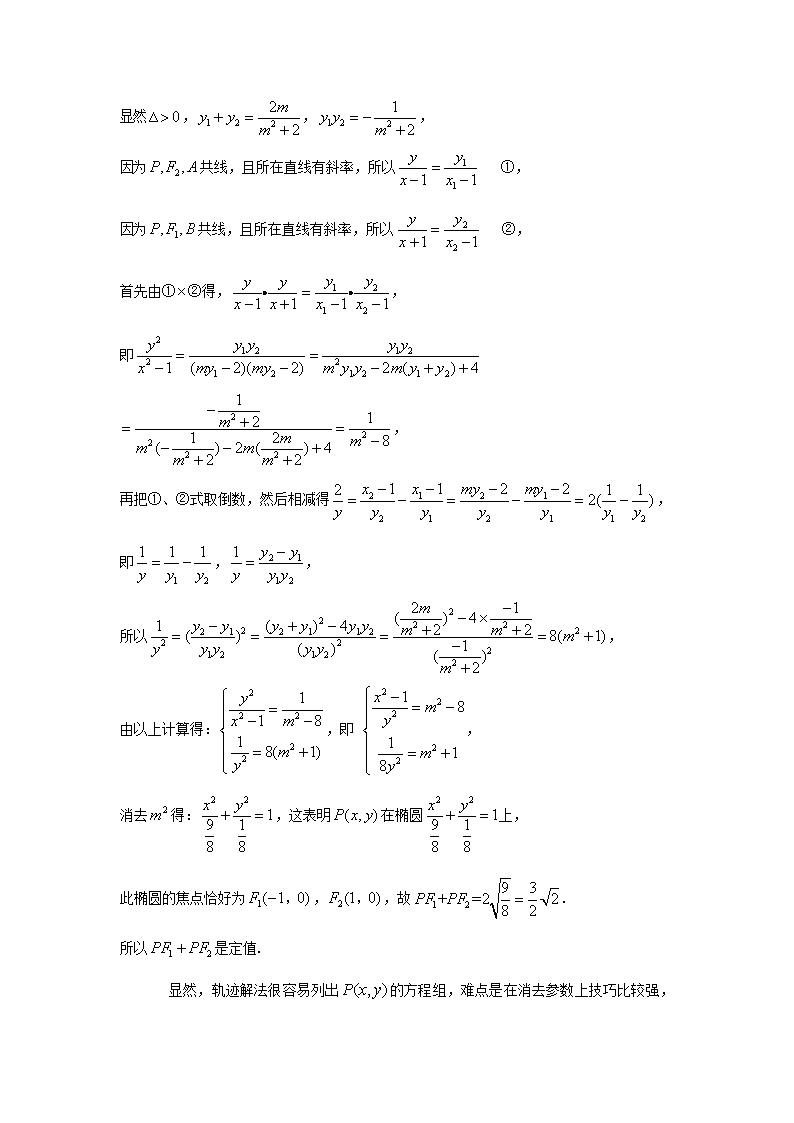
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教A版线段之和(折线段)定值问题探究学案
线段之和(折线段)定值问题探究 2012年江苏卷解析几何题的最后一问,命题组提供的答案充分利用了几何意义.之后,不少杂志上又给出了许多解法,但是这些解法都是利用几何意义找出与的关系.本文换一个视角,利用比较纯粹的代数法先求出点的轨迹方程,再判断点的轨迹为椭圆,然后直接求出是定值. 一、题目: 如图,在平面直角坐标系中,椭圆 的左、右焦点分别为,. 已知和都在椭圆上,其中为椭圆的离心率. (1)求椭圆的方程; (2)设是椭圆上位于轴上方的两点,且直线与直线平行,与交于点P. (i)若,求直线的斜率; (ii)求证:是定值. 二、命题组解法: (1)椭圆的方程为. (2)(ii)由(1)得,,又所以∥, 所以设、的方程分别为,. 所以. 所以 .① 同理,.② 所以∥,所以,即. 所以. 由点在椭圆上知,,所以. 同理,. 所以 由①②得,,, 所以. 所以是定值. 三、轨迹解法: (1)椭圆的方程为. (2)(ii)如右图,设的延长线交椭圆于, 设,,, 由对称性,,其中, 由(1)得,. 设的方程分别为, 由, 显然,,, 因为共线,且所在直线有斜率,所以 ①, 因为共线,且所在直线有斜率,所以 ②, 首先由①②得,, 即 , 再把①、②式取倒数,然后相减得, 即,, 所以, 由以上计算得:,即 , 消去得:,这表明在椭圆上, 此椭圆的焦点恰好为,,故. 所以是定值. 显然,轨迹解法很容易列出 的方程组,难点是在消去参数上技巧比较强,但是这个方法显然是转化为最常规的直线与圆锥曲线位置关系问题(利用根与系数关系问题),体现了解析几何最为基本的转化,整个解题过程体现了转化为通性通法的基本解题思路.查看更多