- 2021-05-09 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020中考数学复习基础小卷速测二十统计与概率相关内容综合
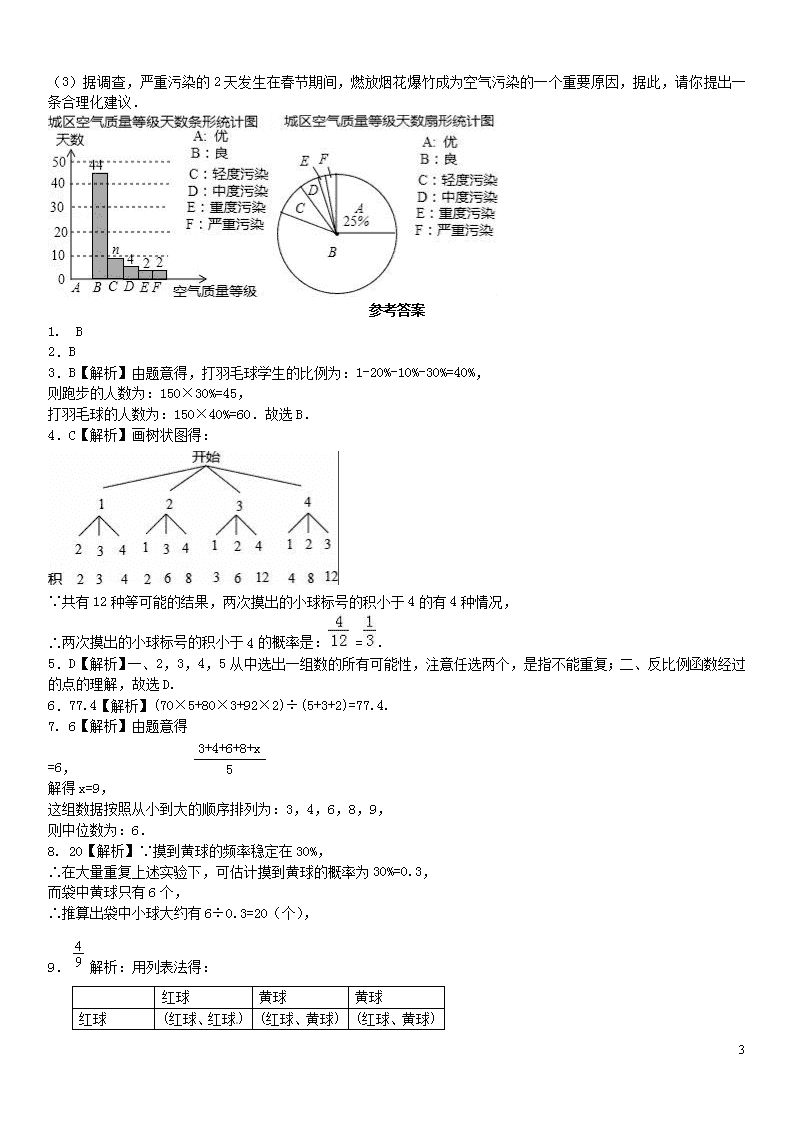
基础小卷速测(二十) 统计与概率相关内容综合 一、选择题 1. 下列调查中,最适合采用全面调查(普查)方式的是( ) A. 对重庆市辖区内长江流域水质情况的调查 B. 对乘坐飞机的旅客是否携带违禁物品的调查 C. 对一个社区每天丢弃塑料袋数量的调查 D.对重庆电视台“天天630”栏目收视率的调查 2.赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图1所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( ) A., B., C., D., 3.某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( ) A.30,40 B.45,60 C.30,60 D.45,40 4. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是( ) A. B. C. D. 5.从2,3,4,5中任意选两个数,记作和,那么点(,)在函数 图象上的概率是( ) A、 B、 C、 D、 二、 填空题 6. 超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下表: 将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是____分. 7.一组数据3,4,6,8,x的平均数是6,则这组数据的中位数是 . 8.一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述试验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球________个. 9.一个布袋内只装有1个红球和2个黄球,这些球除颜色外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黄球的概率是__________. 10.一书架有上下两层,其中上层有2本语文1本数学,下层有2本语文2本数学,现从上下层随机各取1本,则抽到的2本都是数学书的概率为__________. 5 三、解答题 11. 我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题: (1)将条形统计图补充完整. (2)扇形图中的“1.5小时”部分圆心角是多少度? (3)求抽查的学生劳动时间的众数、中位数. 12.小明、小林是三河中学九年级的同班同学。在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并被编入A,B,C三个班,他俩希望能两次成为同班同学。 (1)请你用画树状图法或列举法,列出所有可能的结果; (2)求两人两次成为同班同学的概率. 13.甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示. 根据图中信息,回答下列问题: (1)甲的平均数是__________,乙的中位数是__________. (2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定? 14.某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题: AQI指数 质量等级 天数(天) 0﹣50 优 m 51﹣100 良 44 101﹣150 轻度污染 n 151﹣200 中度污染 4 201﹣300 重度污染 2 300以上 严重污染 2 (1 )统计表中m=__________,n=__________.扇形统计图中,空气质量等级为“良”的天数占 55 %. (2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天? 5 (3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议. 参考答案 1. B 2.B 3.B【解析】由题意得,打羽毛球学生的比例为:1-20%-10%-30%=40%, 则跑步的人数为:150×30%=45, 打羽毛球的人数为:150×40%=60.故选B. 4.C【解析】画树状图得: ∵共有12种等可能的结果,两次摸出的小球标号的积小于4的有4种情况, ∴两次摸出的小球标号的积小于4的概率是: =. 5.D【解析】一、2,3,4,5从中选出一组数的所有可能性,注意任选两个,是指不能重复;二、反比例函数经过的点的理解,故选D. 3+4+6+8+x 5 6.77.4【解析】(70×5+80×3+92×2)÷(5+3+2)=77.4. 7. 6【解析】由题意得 =6, 解得x=9, 这组数据按照从小到大的顺序排列为:3,4,6,8,9, 则中位数为:6. 8. 20【解析】∵摸到黄球的频率稳定在30%, ∴在大量重复上述实验下,可估计摸到黄球的概率为30%=0.3, 而袋中黄球只有6个, ∴推算出袋中小球大约有6÷0.3=20(个), 9.解析:用列表法得: 红球 黄球 黄球 5 红球 (红球、红球) (红球、黄球) (红球、黄球) 黄球 (红球、黄球) (黄球、黄球) (黄球、黄球) 黄球 (红球、黄球) (黄球、黄球) (黄球、黄球) ∵共有9种可能的结果,两次摸出的球都是黄球的情况有4种, ∴两次摸出的球都是黄球的概率为. 10. 【解析】列表如下图: 语 语 数 语 语、语 语、语 语、数 语 语、语 语、语 语、数 数 数、语 数、语 数、数 数 数、语 数、语 数、数 由表格可知,现从上下层随机各取1本,共有12种等可能结果,其中抽到的2本都是数学书的有2种结果, ∴抽到的2本都是数学书的概率为,故答案为. 11. 解:(1)根据题意得:30÷30%=100(人), ∴学生劳动时间为“1.5小时”的人数为100﹣(12+30+18)=40(人), 补全统计图,如图所示: (2)根据题意得:40%×360°=144°, 则扇形图中的“1.5小时”部分圆心角是144°; (3)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时. 12.解:(1)画树状图如下: 5 由树形图可知所以可能的结果为AA,AB,AC,BA,BB,BC,CA,CB,CC; (2)由(1)可知两人再次成为同班同学的概率==. 13.解:(1)甲的平均数==8,乙的中位数是7.5; 故答案为:8;7.5; (2);…(5分)=, =, ∵, ∴乙运动员的射击成绩更稳定. 14.解:(1)∵m=80×25%=20,n=80﹣20﹣44﹣4﹣2﹣2=8, ∴空气质量等级为“良”的天数占:×100%=55%. 故答案为:20,8,55; (2)估计该市城区全年空气质量等级为“优”和“良”的天数共:365×(25%+55%)=292(天), 答:估计该市城区全年空气质量等级为“优”和“良”的天数共292天; 补全统计图: (3)建议不要燃放烟花爆竹. 5查看更多