高考文科数学考试大纲考试说明解读值得借鉴

高考文科数学考试大纲考试说明解读值得借鉴

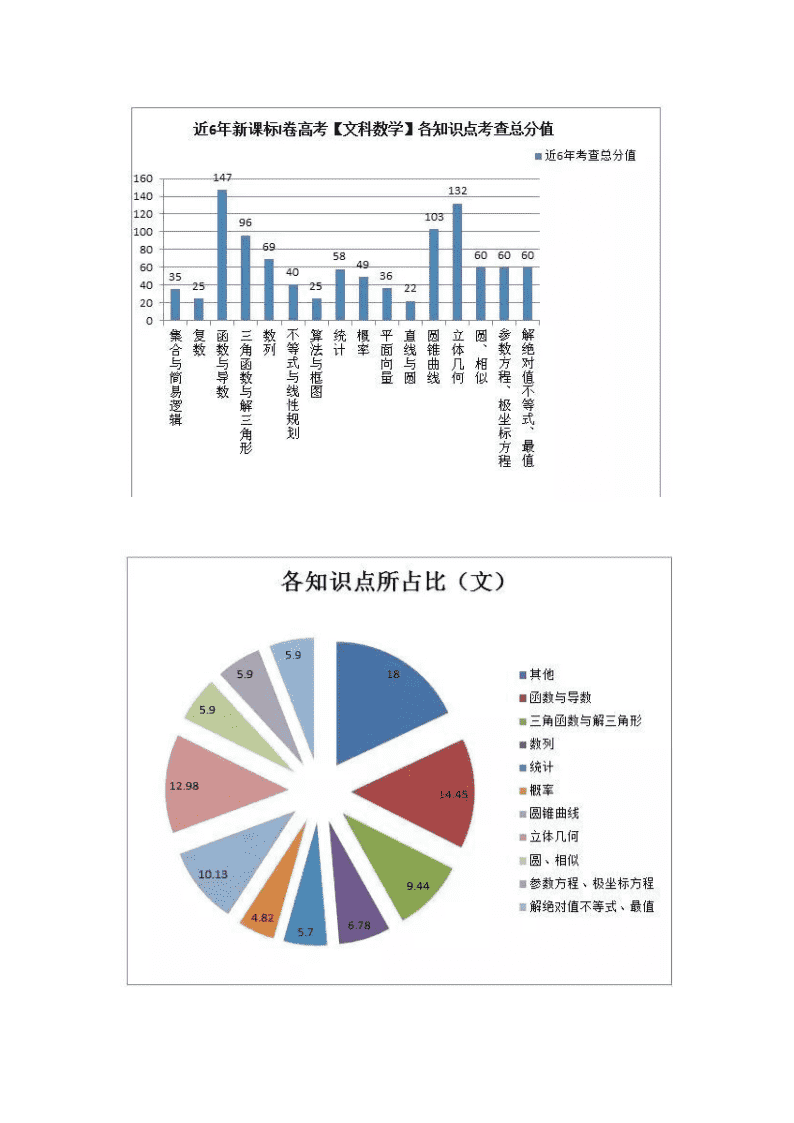
瑞金一中2018届数学（文）考纲、考试说明解读 ‎ ‎ Ⅰ．2018考核目标与要求 一、知识要求 对知识的要求依次是了解、理解、掌握三个层次.‎ 1. 了解：这一层次所涉及的主要行为动词有：了解,知道、识别,模仿,会求、会解等. ‎ ‎2.理解：这一层次所涉及的主要行为动词有：描述,说明,表达,推测、想象,比较、判别,初步应用等.‎ ‎3.掌握：这一层次所涉及的主要行为动词有：掌握、导出、分析,推导、证明,研究、讨论、运用、解决问题等.‎ 二、能力要求 能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.‎ Ⅱ．2018考试范围与要求 从试卷结构上，全国卷分为必考和选考两部分，必考部分包括12个选择题，4个填空题和5个解答题；选考部分包括选修系列4的“坐标系与参数方程”“不等式选讲”各1个解答题，考生从2题中任选1题作答，若多做，则按所做的第一题给分。‎ Ⅲ 与2017年考纲和说明对比解读如下 一：与2017年考试大纲对比，考核目标，考核范围、考核要求都没有变化还是知识要求（了解、理解、掌握）都没变化，考核能力（空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.）也没有变化，一句话什么也没变化。这说明2018年数学高考仍然以平稳过渡，“稳中求变” “变中求新”“新中求活” “活中求能”‎ 二、预计2018年的高考全国卷难度基本持平，选择填空难度会略有上升，对于题目的文字理解和运算方面会加强，运算方面主要是式子的组合变形与分解变形以及对几何图形各几何量的计算。‎ 三、高考数学难题的设置方式 高考数学试题中的难题一般会以三种方式呈现：‎ 第一类：题目设置较长文字较多，会设计一些背景材料，在考试时间紧张的情况下会对考生心理造成很大压力。‎ 第二类:题目较短主要以各类式子或不等式呈现，考察学生的观察问题分析角度以及各类具体组合变形方法的掌握.‎ 第三类:思考列式较简单，但计算过程无法顺利进行，往往需要一些技巧。‎ 四、高考数学试卷基本结构特点 目前全国卷数学共22道题目，其中选择12道，填空4道，解答6道，其中一道为二选一。‎ 高考数学选择填空每年基本有5个左右固定的考点，其余11个左右考点每年不是太固定，但总的基本考点有33个左右。下面对高考数学解答题基本命题趋势做一简单分析：‎ 解答题数列:命题基本以等差与等比数列形成的交叉为主，同时会融入一些创新点，求解这些新复杂数列的和、通项以及不等式证明。‎ 解答题解三角形:命题以含有角或边的三角等式以及三角形图形为主，求解边，角以及面积或某些含有边和角的式子范围或最值。‎ 解答题空间几何:以三棱锥和四棱柱切入，考察平行、垂直以及夹角、体积的计算 解答题概率统计:避开热点话题材料，以大家都熟知的某些材料或图表为切入点考察概率的计算方法以及一些基本的数字特征计算。‎ 解答题圆锥曲线:以椭圆方程、离心率求解以及图形中某些量或者题目中的未知量的范围最值求解为主要目标，考察几何问题的基本思考方法和运算方法，属于压轴题目。‎ 解答题导数:以基本概念和各类含参不等式或特殊不等式为目标，考察复杂函数的参数范围求解方法，属于压轴题目。‎ 解答题二选一参数方程:以圆、椭圆，抛物线为主以不同坐标或不同方程形式下的各几何量的简单计算。属于简单考生必须拿满分的题目。‎ 解答题二选一不等式:以各类含参不等式为主，间接考察函数与基本不等式的应用。‎ 五、高考数学高频命题点解读 下面梳理了全国卷近几年各考点分值比重情况，通过这些统计图表我们可以看出高考的侧重点，分值比重以及热门命题点，帮助我们在高考复习中有侧重点的分配时间和学习精力。下面为2017年全国卷使用情况（）‎ 全国Ⅰ卷地区：福建、河南、河北、山西、江西、湖北、湖南、广东、安徽 六、高考数学新题型 创新作为整个社会的主流，在高考数学的命题中也不例外，每年都会出现两三道具有创新理念的题目，基本会以数学文化或者单独的解题方法或运算过程中的创新出现。‎ 一般创新思维有八种模式：第一、延伸式思维，第二、扩展式思维，第三、联想式思维，第四、运用式思维，第五、逆向式思维，第六、幻想式思维，第七、奇异式思维，第八、综合式思维。‎ 创新方式：1.题目中解题方法的创新 2.题目中引入创新符号