2009年泉州市洛江区初中学业质量检查数学试题

2009年泉州市洛江区初中学业质量检查数学试题

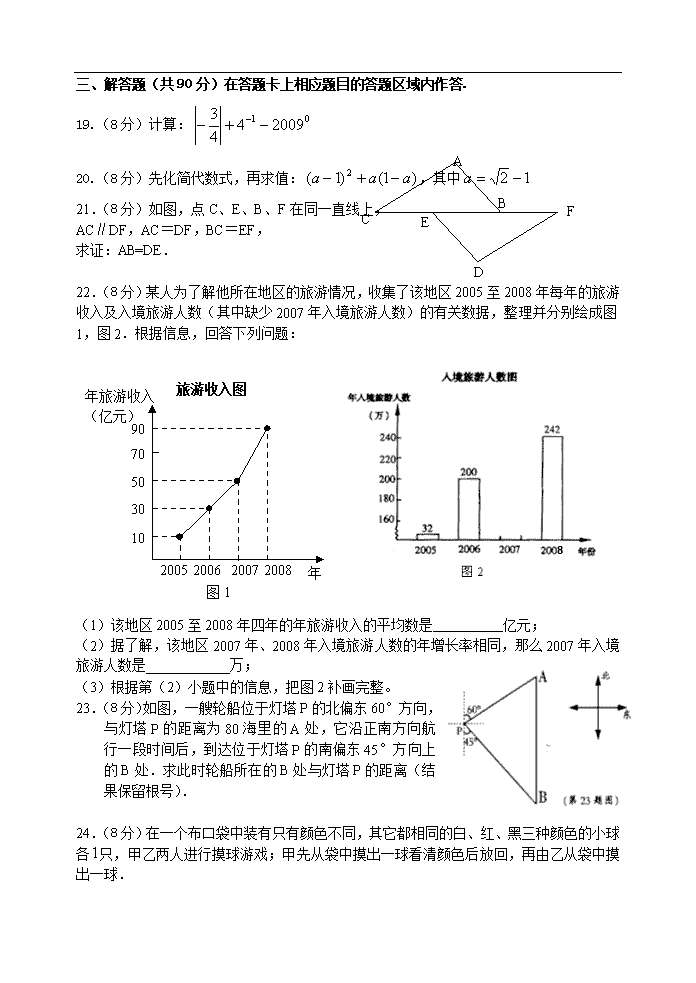
2009 年洛江区初中学业质量检查 数 学 试 题 （满分：150 分；考试时间：120 分钟） 一、选择题（每小题 4 分，共 24 分）请在答题卡上相应题目的答题区域内作答 1. 计算:7–9 =( ). A．–2 B.2 C.-16 D. 16 2．一组数据-2，1，0，-1，2 的极差是（ ） A．2 B．４ Ｃ．３ Ｄ．1 3．将如图所示放置的一个直角三角形 ABC（∠C=90°），绕斜边 AB 旋转一周，所得到的几 何体的正视图是下面四个图中的（ ） A．　　　　Ｂ．　　　　Ｃ．　　　　　Ｄ． 4.如图，圆弧形桥拱的跨度 AB＝12 米，拱高 CD＝4 米， 则拱桥的半径为（ ） 　　A．6.5 米　　　B．9 米　　　C．13 米　　　D．15 米 5．不等式组 的解集为( ). A．χ＜ 6 B. χ＜-2 C. –2＜χ＜6 D.无解 6．如图，三个大小相同的正方形拼成六边形 ，一动点 从点 出发沿着 → → → → 方向匀速运动，最后到达点 .运动过程中 的面积（ ）随时间（t） 变化的图象大致是（ ） 二、填空题（每小题3分，共36分）在答题卡上相应题目的答题区域内作答. 7．计算： ＝　　　　． 8. 分解因式： ____________. 9．据有关资料显示，长江三峡工程电站的总装机容量是 18 200 000 千瓦，用科学记数法 ABCDEF P A A B C D E E PEF∆ s    − 2 6 x＜ x＜ 32 )(a =− xyx 23 第 4 题图 s t A． 。 O s t B O s D O s t C O t （第 6 题图） A B C D E . F . P . · α 表示应记为 千瓦. 10.某商品原售价是 元，则提价 10﹪后售价为 元. 11．计算： =__________ 12. 一个 n 边形的内角和等于 720°，那么这个多边形的边数 n＝ . 13. 一副三角板，如图所示叠放在一起，则图中∠α的度数是 . 第 13 题图 第 14 题图 第 15 题图 14．如图，如果从半径为 9cm 的圆形纸片剪去 圆周的一个扇形，将留下的扇形围成一个 圆锥（接缝处不重叠），那么这个圆锥的高为 ㎝。 15．共有 12 个大小相同的小正方形，其中阴影部分的 5 个小正方形是一个正方体的表面 展开图的一部分．现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表 面展开图的概率是 ． 16．反比例函数 的图象在第二象限与第 象限. 17．如图,在菱形 ABCD 中，P、Q 分别是 AD、AC 的中点，如果 PQ=3，那么菱形 ABCD 的周长是 第 17 题图 第 18 题图 18．如图，已知直角三角形 ， ， ，过直角顶点 作 ，垂 足为 ，再过 作 ，垂足为 ；过 作 ，垂足为 ，再过 作 ，垂足为 ；……，这样一直做下去，得到了一组线段 ， ， ，……，则第 10 条线段 ． 三、解答题（共 90 分）在答题卡上相应题目的答题区域内作答. a 2 4 2 2 m m m −− − 1 3 xy 3−= ACB 3AC = 4BC = C 1CA AB⊥ 1A 1A 1 1AC BC⊥ 1C 1C 1 2C A AB⊥ 2A 2A 2 2A C BC⊥ 2C 1CA 1 1AC 1 2C A 5 5A C = A CB A1 A2 A3A4A5 C1C2C3C4C5 19.（8 分）计算： 20.（8 分）先化简代数式，再求值： ，其中 21．（8 分）如图，点 C、E、B、F 在同一直线上， AC∥DF，AC＝DF，BC＝EF， 求证：AB=DE. 22．（8 分）某人为了解他所在地区的旅游情况，收集了该地区 2005 至 2008 年每年的旅游 收入及入境旅游人数（其中缺少 2007 年入境旅游人数）的有关数据，整理并分别绘成图 1，图 2．根据信息，回答下列问题： （1）该地区 2005 至 2008 年四年的年旅游收入的平均数是 亿元； （2）据了解，该地区 2007 年、2008 年入境旅游人数的年增长率相同，那么 2007 年入境 旅游人数是 万； （3）根据第（2）小题中的信息，把图 2 补画完整。 23．（8 分）如图，一艘轮船位于灯塔 P 的北偏东 60°方向， 与灯塔 P 的距离为 80 海里的 A 处，它沿正南方向航 行一段时间后，到达位于灯塔 P 的南偏东 45°方向上 的 B 处．求此时轮船所在的 B 处与灯塔 P 的距离（结 果保留根号）． 24．（8 分）在一个布口袋中装有只有颜色不同，其它都相同的白、红、黑三种颜色的小球 各 只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸 出一球． （1）试用树状图（或列表法）表示摸球游戏所有可能的结果； 01 200944 3 −+− − )1()1( 2 aaa −+− 12 −=a 2005 2006 2007 2008 年 年旅游收入 （亿元） 90 70 50 30 10 图 1 旅游收入图 1 A B FEC D （2）如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的 概率. 25．（8 分）如图，正方形网格中的每个小正方形的边长都是 1，每个 小正方形的顶点叫做格点． 的三个顶点 都在格点 上． （1）画出 绕点 逆时针旋转 后得到的三角形； （2）求 在上述旋转过程中所扫过的面积． 26．（8 分）已知：如图，反比例函数 y=－ 与一次函数 y= －x+2 的图像交于 A，B 两点，求： （1）A、B 两点的坐标； （2）△AOB 的面积． 27．（１３分）我区某工艺厂为迎接建国 60 周年，设计 了一款成本为 20 元 ∕ 件的工艺品投放市场进行试 销．经过调查，其中工艺品的销售单价 （元 ∕ 件） 与每天销售量 （件）之间满足如图所示关系． （1）请根据图象直接写出当销售单价定为 30 元和 40 元时相应的日销售量； （2）①试求出 与 之间的函数关系式； ②若物价部门规定，该工艺品销售单价最高不能超 过 45 元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？ 最大利润是多少？（利润=销售总价－成本总价）。 28. （8 分）已知直线 与 轴 轴分别交于点 A 和点 B，点 B 的坐标为（0，6） （1）求的 值和点 A 的坐标； （2）在矩形 OACB 中，点 P 是线段 BC 上的一动点，直线 PD ⊥AB 于点 D，与 轴交于点 E，设 BP= ，梯形 PEAC 的面积 为 。 ①求 与 的函数关系式，并写出 的取值范围； ②⊙Q 是△OAB 的内切圆，求当 PE 与⊙Q 相交的弦长为 2.4 时点 P 的坐标。 ABO△ A B O， ， ABO△ O 90 ABO△ 8 x x y y x mxy +−= 4 3 x y m x a s s a a （第 25 题） A B O 四、附加题：（共 10 分）在答题卡上相应题目的答题区域内作答。 友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况。如 果你全卷得分低于 90 分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最 多不超过 90 分；如果你全卷总分已经达到或超过 90 分，则本题的得分不计入全卷总分。 1．（5 分）填空：在△ABC 中， ， ，则 = 。 2．（5 分）计算： = 。 考生信息 一、选择题 二、填空题 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19．解：原式= 20．解： 60=∠A 100=∠B C∠ ababab 753 +− 21．解： 22．解：（1） 亿元。 （2） 万。 请勿在此处作任何标记 23.解: A B FEC D 24.解: 25．解：（1） （2） 考生信息 26.解: （第 25 题） A B O 27．解： 请勿在此处作任何标记 28.解: 四、附加题 1． 2. 2009 年洛江区初中学业质量检查 数学试题参考答案及评分标准 一、选择题（每小题 4 分，共 24 分） 1．A 2．B 3．Ｃ　　　4．Ａ　　　5．Ｂ　　　6．Ｂ 二、填空题（每小题 3 分，共 36 分） 　7． 　 8． 　 9． 　10． 11．2　 12．6 13． 　　　　 14． 　　15． 　　　16．四　 17．24 18． 三、解答题（共 90 分） 19.（8 分）解:原式= （化简正确每个得 2 分）………………………………6 分 =0…………………………………………………………………… 8 分 20．（8 分）解：原式= ………………………………………………4 分 = ………………………………………………………………5 分 当 时，原式= …………………………………… 6 分 = …………………………………………8 分 21．（8 分）证明：∵AC∥DF ∴ ………………………………………………………… 3 分 在 ∴ ≌ ……………………………………………………6 分 ∴ AB=DE………………………………………………………………8 分 22．（8 分） 解: (1) 45………………………………… 3 分 （2）220…………………………………… 6 分 （3）补画图开如左图所示。………………8 分 23．（8 分） 6a )3( yxx − 71082.1 × a1.1 °75 53 7 4 10)5 4(3× 14 1 4 3 −+ 22 12 aaaa −++− 1+− a 12 −=a 1)12( +−− 22 +− FC ∠=∠ 中和 DFEACB ∆∆    = ∠=∠ = EFBC FC DFAC ACB∆ DFE∆ 解：作 点， 则 AP=80 海里………2 分 在 Rt ……………………3 分 ∴ （海里）…………5 分 在 Rt ……………………6 分 ∴ （海里） 答：略……………………………………………8 分 24.（8 分解：（1）树状图如下 甲摸到的球 白 红 黑 ……………………5 分 乙摸到的球 白 红 黑 白 红 黑 白 红 黑 列表如下：（参照树状图相应给分） 甲 乙 白 红 黑 白 白，白 红，白 黑，白 红 白，红 红，红 黑，红 黑 白，黑 红，黑 黑，黑 （2）乙摸到与甲相同颜色的球有三种情况 乙能取胜的概率为 ………………………………………………………………8 分 25．（8 分） （1）画图正确（如图）．………………………………………4 分 （2） 所扫过的面积是： ．…………8 分 26．（8 分（1）由 ，解得 ， AOB△ AOBDOBS S S= + △扇形 290 π 4 4 4π 4360 = × + = + 8 2 y x y x  = −  = − + 1 1 4 2 x y =  = − 1 1 2 4 x y = −  = CABPC 于⊥ °° =∠=∠ 45,30 BPCAPC PA PCAPC，APC =∠∆ cos中 340cos =∠⋅= APCPAPC PB PCBPC，PCB =∠∆ cos中 64045cos 340 cos ==∠= °BPC PCPB ∴ 3 1 9 3 = C D E （第 25 题） A B O ∴A（－2，4），B（4，－2）．……………………………………………………4 分 （2）当 y=0 时，x=2，故 y=－x+2 与 x 轴交于 M（2，0），∴OM=2．………6 分 ∴S△AOB=S△AOM +S△BOM = OM·│yA│+ OM·│yB│= ×2×4+ ×2×2=4+2=6． ……………………………………………………………………8 分 27．（1）500 件和 400 件；…………………………………………………………… 4 分 （2）①设这个函数关系为 = + ∵这个一次函数的图象经过（30，500）、（40，400）这两点， ∴ 解得 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 ∴函数关系式是： =－10 +800 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ②设工艺厂试销该工艺品每天获得的利润是 W 元，依题意得 W=（ －20）（－10 +800）∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 =－10（ －50） +9000 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 ∵－10＜0，∴函数图象为开口向下的抛物线（函数草图略） 其对称轴为 x=50，又 20< ≤45 在对称轴的左侧，W 的值随着 值的增大而增大 ∴当 x=45 时，W 取得最大值，W 最大=－10（45－50） +9000=8750 答：销售单价定为 45 元∕件时，工艺厂试销该工艺品每天获得的利润最大，最大利润为 8750 元。………………………………………………………………………………………… 13 分 28．（13 分）解：（1）把 B（0，6）代入 ，得 ＝6………………………1 分 把 ＝0 代入 ，得 ＝8 ∴点 A 的坐标为（8，0）…………… 3 分 （2）在矩形 OACB 中，AC＝OB＝6， BC＝OA＝8，∠C＝90° ∴AB＝ …………………………4 分 ∵PD⊥AB ∴∠PDB=∠C＝90° 1 2 1 2 1 2 1 2 y k x b 500 30 400 40 k b k b = +  = + 10 800 k b = −  = y x x x x 2 x x 2 my +−= 4 3 m y 64 3 +−=y x 1086 2222 =+=+ BCAC BA BC BP BDCBA ==∠cos ∴ ∴ ∴ ……………………………………………………………………………5 分 又∵BC∥AE ∴△PBD∽△EAD ∴ ，即 ∴ ……………………………………………………………6 分 ∵ ∴ （ ）……………………………7 分 （注：写成 不扣分） ② ⊙Q 是△OAB 的内切圆 ，可设⊙Q 的半径为 r ∵ ,解得 r=2.………………………………………8 分 设⊙Q 与 OB、AB、OA 分别切于点 F、G、H 可知，OF＝2 ∴BF＝BG＝OB－OF＝6－2＝4……………………………………………………………9 分 设直线 PD 与⊙Q 交于点 I、J ，过 Q 作 QM⊥IJ 于点 M，连结 IQ、QG ∵QI＝2， ∴ ………………………………………………………10 分 ∴ 在矩形 GQMD 中，GD＝QM＝1.6 ∴BD＝BG+GD＝4+1.6＝5.6 由 得 ∴点 P 的坐标为（7，6）…………………………………………………………………11 分 当 PE 在圆心 Q 的另一侧时，同理可求点 P 的坐标为（3，6）………………………12 分 综上，P 点的坐标为（7，6）或（3，6）．………………………………………………13 分。 10 8= a BD aBD 5 4= aAD 5 410 −= BD AD BP AE = 5 4 5 410 a a a AE − = aaAE −=−= 5.12)5 410(4 5 ACAEPCS PEAC )(2 1 +=梯形 5.6166)5.128(2 1 +−=−+−= aaas 8<≤ ao 8<< ao 862 1)1086(2 1 ××=++=∆ rS OAB 2.12 1 == IJIM 6.122 =−= IMQIQM 10 8cos ===∠ BA BC BP BDCBA 74 5 == BDBP 四、附加题：（共 10 分）。 1．（5 分） = 2．（5 分）C∠ °20 ab5