- 2021-05-08 发布 |
- 37.5 KB |
- 29页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习第1讲 空间几何体的三视图、表面积与体积课件(全国通用)
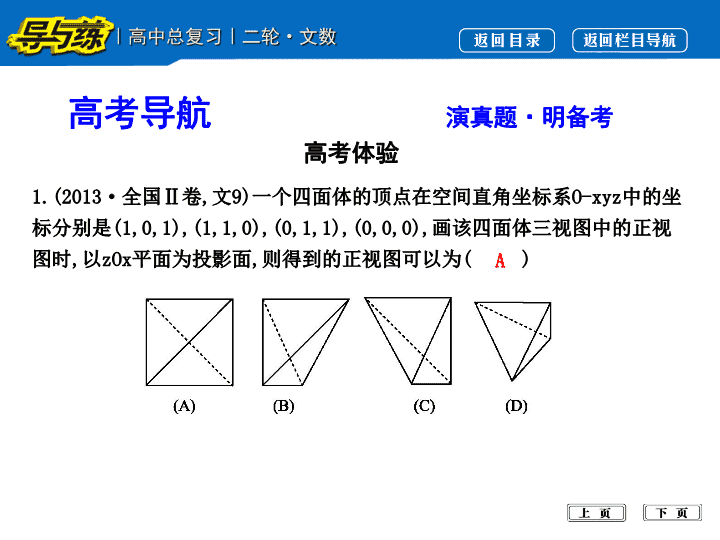
专题五 立体几何 第 1 讲 空间几何体的三视图、表面积与体积 热点突破 高考导航 备选例题 高考导航 演真题 · 明备考 高考体验 1. (2013· 全国 Ⅱ 卷 , 文 9) 一个四面体的顶点在空间直角坐标系 O - xyz 中的坐标分别是 (1,0,1),(1,1,0),(0,1,1),(0,0,0), 画该四面体三视图中的正视图时 , 以 zOx 平面为投影面 , 则得到的正视图可以为 ( ) A 解析 : 在空间直角坐标系中作出四面体 OABC 的直观图如图所示 , 作顶点 A 、 C 在 zOx 平面的投影 A′,C′, 可得四面体的正视图 . 故选 A. 2. (2014· 全国 Ⅰ 卷 , 文 8) 如图 , 网格纸的各小格都是正方形 , 粗实线画出的是一个几何体的三视图 , 则这个几何体是 ( ) (A) 三棱锥 (B) 三棱柱 (C) 四棱锥 (D) 四棱柱 B 解析 : 由题三视图得直观图如图所示 , 为三棱柱 . 故选 B. 3. (2012· 新课标全国卷 , 文 7) 如图 , 网格纸上小正方形的边长为 1, 粗线画出的是某几何体的三视图 , 则此几何体的体积为 ( ) (A)6 (B)9 (C)12 (D)18 B 4. (2015· 全国 Ⅱ 卷 , 文 6) 一个正方体被一个平面截去一部分后 , 剩余部分的三视图如图 , 则截去部分体积与剩余部分体积的比值为 ( ) D 5. (2016· 全国 Ⅰ 卷 , 文 7) 如图 , 某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径 . 若该几何体的体积是 , 则它的表面积是 ( ) (A)17π (B)18π (C)20π (D)28π A 6. (2015· 全国 Ⅰ 卷 , 文 11) 圆柱被一个平面截去一部分后与半球 ( 半径为 r) 组成一个几何体 , 该几何体三视图中的正视图和俯视图如图所示 . 若该几何体的表面积为 16+20π, 则 r 等于 ( ) (A)1 (B)2 (C)4 (D)8 解析 : 由已知可知 , 该几何体的直观图如图所示 , 其表面积为 2πr 2 +πr 2 +4r 2 +2πr 2 =5πr 2 +4r 2 . 由 5πr 2 +4r 2 =16+20π, 得 r=2. B A 高考感悟 1. 考查角度 (1) 由网格图给出三视图或由空间直角坐标系给出几何体 . (2) 由三视图还原直观图求线段的长度、面积、体积等 . (3) 与球有关的“接”“切”问题 . 2. 题型及难易度 选择题、填空题 , 中、低档 . 热点突破 剖典例 · 促迁移 空间几何体的三视图 热点一 【 例 1】 (2016· 天津卷 , 文 3) 将一个长方体沿相邻三个面的对角线截去一个棱锥 , 得到的几何体的正视图与俯视图如图所示 , 则该几何体的侧视图为 ( ) 考向 1 几何体三视图的识别 解析 : 由几何体的直观图知选 B. 考向 2 几何体三视图的相关计算 【 方法技巧 】 由三视图还原到直观图的思路 (1) 根据俯视图确定几何体的底面 . (2) 根据正视图或侧视图确定几何体的侧棱与侧面的特征 , 调整实线和虚线所对应的棱、面的位置 . (3) 确定几何体的直观图形状 . 熟练掌握常见简单几何体及其组合体的三视图 , 特别是正方体、长方体、圆柱、圆锥、三棱柱、三棱锥等几何体的三视图是解决此类问题的基础 . 热点训练 1:(1) 在一个几何体的三视图中 , 正视图和俯视图如图所示 , 则相应的侧视图可以为 ( ) 解析 : (1) 由题目所给的几何体的正视图和俯视图 , 可知该几何体为半圆锥和三棱锥的组合体 , 可知侧视图为等腰三角形 , 且轮廓线为实线 , 故选 D. (2) (2015· 北京卷 , 文 7) 某四棱锥的三视图如图所示 , 该四棱锥最长棱的棱长为 ( ) 空间几何体的表面积和体积 热点二 考向 1 空间几何体的表面积 【 例 3】 (2016· 全国 Ⅱ 卷 , 文 7) 如图是由圆柱与圆锥组合而成的几何体的三视图 , 则该几何体的表面积为 ( ) (A)20π (B)24π (C)28π (D)32π 考向 2 空间几何体的体积 【 例 4】 (2016· 山东卷 , 文 5) 一个由半球和四棱锥组成的几何体 , 其三视图如图所示 , 则该几何体的体积为 ( ) 答案 : (1)C (2) (2016· 北京卷 , 文 11) 某四棱柱的三视图如图所示 , 则该四棱柱的体积为 . 多面体与球的切接问题 热点三 (2) (2015· 全国 Ⅱ 卷 , 文 10) 已知 A,B 是球 O 的球面上两点 ,∠AOB=90°,C 为该球面上的动点 . 若三棱锥 OABC 体积的最大值为 36, 则球 O 的表面积为 ( ) (A)36π (B)64π (C)144π (D)256π 【 方法技巧 】 多面体与球接、切问题的求解策略 (1) 确定球心的位置 , 弄清球的半径 ( 直径 ) 与该几何体已知量的关系 , 列方程 ( 组 ) 求解 . (2) 补成正方体、长方体、正四面体、棱柱等规则几何体求解 . 热点训练 3: 某几何体的三视图如图 , 若该几何体的所有顶点都在一个球面上 , 则该球面的表面积为 ( ) 备选例题 挖内涵 · 寻思路 【 例 3】 正四面体 ABCD 的棱长为 4,E 为棱 BC 的中点 , 过 E 作其外接球的截面 , 则截面面积的最小值为 . 答案 : 4π 点击进入 限时训练查看更多