江苏省启东市2019-2020学年高一第二学期期末调研测试数学试题

江苏省启东市2019-2020学年高一第二学期期末调研测试数学试题

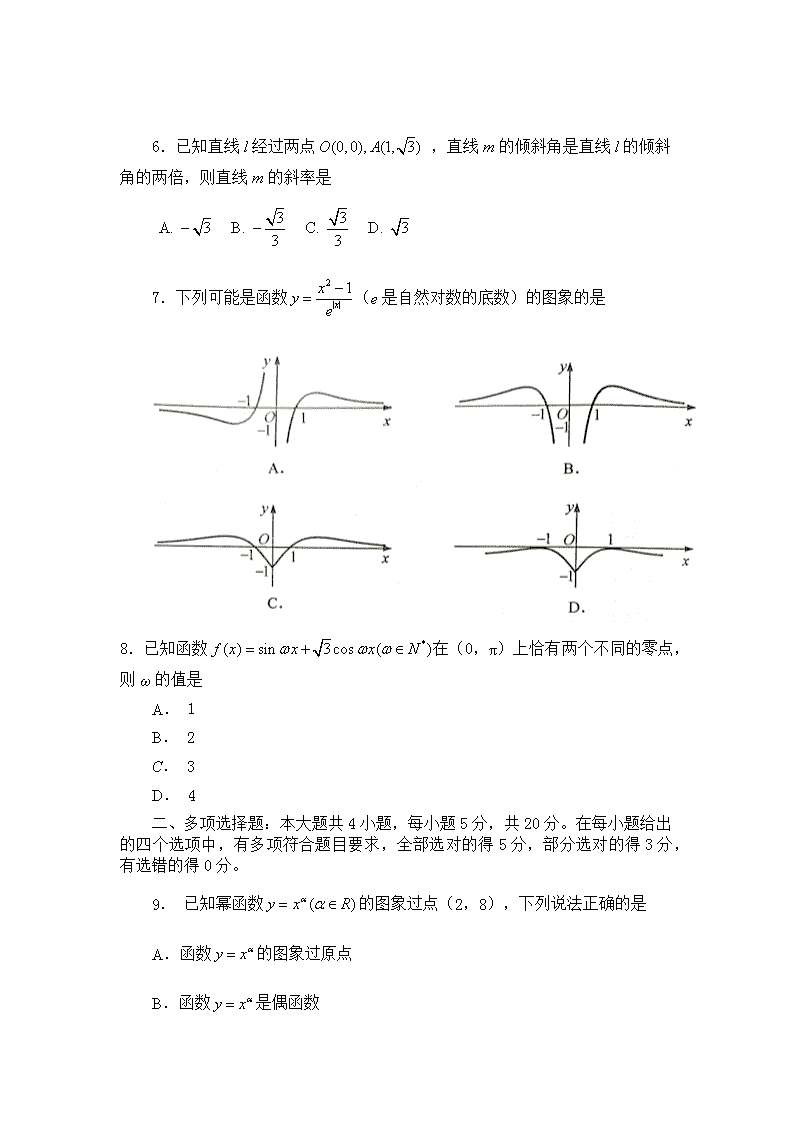
2019 ～2020 学年第二学期期末调研测试 高一数学试题 一、单项选择题：本大题共 8 小题，每小题 5 分，共 40 分。在每小题给出 的四个选项中，只有一个是符合题目要求的。 1． 已知集合 ，则 2． 已知向量 ，且 ，则 x＝ 3．已知一只口袋内装有大小相同的 4 只球，其中 2 只白球， 2 只黑球，从 中一次摸出 2 只球，则摸出的 2 只球中至少有 1 只是白球的概率是 4．已知 ，则 a， b， c 的大小关系是 5．为了估计加工零件所花费的时间，为此进行了 4 次试验，测得的数据如 下表； 若零件数 x 与加工时间 y 具有线性相关关系，且线性回归方程为 ， 则 a＝ A． 1 B． 0．8 C． 1．09 D． 1．5 { | 2 0}, {1,2,3}A x x B= − ≤ = I A B = A. B. {1} C. {1,2} D. {1,2,3}∅ (1, ), (4,2)x= =a b a b 21 1 A. 2 B. C .. 2 2 D− − 1 1 2 5. B. C. 6 3 3 6D.A 0.5 2 0.5log 2, 2 , 0.5a b c= = = A. B. C. D. a b c a c b b c a c b a< < < < < < < < ˆ 0.36 0.01y x= + 6．已知直线 l 经过两点 ，直线 m 的倾斜角是直线 l 的倾斜 角的两倍，则直线 m 的斜率是 7．下列可能是函数 （e 是自然对数的底数）的图象的是 8．已知函数 在（0，π）上恰有两个不同的零点， 则 ω 的值是 A． 1 B． 2 С． 3 D． 4 二、多项选择题：本大题共 4 小题，每小题 5 分，共 20 分。在每小题给出 的四个选项中，有多项符合题目要求，全部选对的得 5 分，部分选对的得 3 分， 有选错的得 0 分。 9． 已知幂函数 的图象过点（2，8），下列说法正确的是 A．函数 的图象过原点 B．函数 是偶函数 (0,0), (1, 3)O A 3 3 A. 3 B. C. D. 33 3 − − 2 | | 1 x xy e −= *( ) sin 3 cos ( )f x x x Nω ω ω= + ∈ ( )y x Rα α= ∈ y xα= y xα= C．函数 是单调减函数 D．函数 的值域为 R 10．某人射箭 9 次，射中的环数依次为： 7， 8， 9， 7， 6， 9， 8， 10， 8，关于这组数据，下列说法正确的是 A．这组数据的众数是 8 B．这组数据的平均数是 8 C．这组数据的中位数是 6 D．这组数据的方差是 11． 已知直线 l： ，其中 ，下列说法正确的是 A．当 a＝－1 时，直线 l 与直线 x＋y＝0 垂直 B．若直线 l 与直线 x－y＝0 平行，则 a＝0 C．直线 l 过定点(0，1) D．当 a＝0 时，直线 l 在两坐标轴上的截距相等 12．已知在三棱锥 P—ABC 中， AP， AB， AC 两两互相垂直， AP＝ 5cm， AB＝4cm，AC＝3cm，点 O 为三棱锥 P—ABC 的外接球的球心，点 D 为△ ABC 的外接圆的圆心，下列说法正确的是 A．三棱锥 P—ABC 的体积为 10 cm3 B．直线 BC 与平面 PAC 所成角的正切值为3 4 C．球 O 的表面积为 50πcm2 D． OD⊥PA 三、填空题：本大题共 4 小题，每小题 5 分，共 20 分。 13．式子 的值是________ 14．已知 为锐角，则 ________ 15．已知直线 x－y＋1＝0 与圆 相切，则 a 的值是________ 16． “辛普森（Simpson）公式”给出了求几何体体积的一种估算方法：几何 体的体积 V 等于其上底的面积 S、中截面（过几何体高的中点平行于底面的截面） 的面积 S0 的 4 倍、下底的面积 S'之和乘以高 h 的六分之一，即 y xα= y xα= 4 3 2( 1) 1 0a a x y+ + − + = a R∈ 1 2 39 log 27+ 3sin ,5 α α= cos( )π α− = 2 2 2 0x y x a+ − − = ．已知函数 的图象过点 ， 与直线 x＝0，y＝1 及 y＝2 围成的封闭图形绕 y 轴旋转一周得到一个几何体，则 k －m＝________，利用“辛普森（Simpson）公式"可估算该几何体的体积 V ＝ ________ （第一空 2 分，第二空 3 分） 四、解答题：本大题共 6 小题，共 70 分。解答时应写出文字说明、证明过 程或演算步骤。 17． （本小题满分 10 分） 已知 的夹角为π 6． 求： ； （2） ． 18．（本小题满分 12 分） 眼睛是心灵的窗户，保护好视力非常重要， 某校高一、高二、高三年级分别有学生 1200 名、 1080 名、720 名．为了解全校学生的视力情况， 学校在 6 月 6 日“全国爱眼日”采用分层抽样的方法， 抽取 50 人测试视力，并根据测试数据绘制了如 图所示的频率分布直方图。 （1） 求从高一年级抽取的学生人数； （2）试估计该学校学生视力不低于 4．8 的 概率； (3)从视力在[4．0，4．4)内的受测者中随机 抽取 2 人，求 2 人视力都在[4．2，4．4）内的概 率． 19． （本小题满分 12 分） 如图，在长方体 中，已知 AB＝AD＝1， AA1＝2． （1）求证：BD⊥平面 A1ACC1； (2)求二面角 的正切值． 20．（本小题满分 12 分） 在锐角△ABC 中，设角 A， B， C 所对的边长分别为 a， b， c，且 ． 0 1 ( 4 )6V h S S S ′= + + ( 0)ky m xx = + > 1( ,2), (1,1)2A B | | 3,| | 1,= = 与a b a b +⋅（ ）a a b -2a b 1 1 1 1ABCD A B C D− 1A BD A− − 3sin 2b A a= （1）求 B 的大小； （2）若 ，点 D 在边 AC 上，________，求 BD 的长． 请在①AD＝DC； ② ∠DBC＝∠DBA； ③BD⊥AC这三个条件中选择一个， 补充在上面的横线上，并完成解答． （注：如果选择多个条件分别解答， 则按第一个解答计分）． 21． （本小题满分 12 分） 已知圆 关于直线 对称 （1）求实数 a 的值； (2)设直线 与圆 C 交于点 A，B，且 ． ①求 k 的值； ②点 P（3，0），证明：x 轴平分∠APB． 22．（本小题满分 12 分） 已知函数 f（x）， g（x）分别是定义在 R 上的偶函数和奇函数， 且 ． (1)求函数 f(x)与 g(x)的解析式； （2）设函数 ，若对任意实数 x， 恒成立， 求实数 a 的取值范围． 32, 2AB BC= = 2 2 2 2 3 0x y x ay+ + − − = : 2 1 0l x y− + = (( 0)y kx k= > 8 5 5AB = 2( ) ( ) 1f x g x x x+ = − + ( ) ( ) | ( ) 1|G x f x a g x= + + 3( ) 2G x ≥ 数学参考答案与评分建议 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分。 1~4 C C D B 5~8 B A C B 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分。 9. AD 10. ABD 11. AC 12. ABC 三、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13. 6 14． 15．1 16． 1， 109π 216 四、解答题：本大题共 6 小题，共计 70 分． 17. （本小题满分 10 分） 已知 ， ， 与 的夹角为 ． 求：（1） ； （2） ． 解：（1） ……2 分 ． ……5 分 （2） ……7 分 ． ……10 分 18. （本小题满分 12 分） 眼睛是心灵的窗户，保护好视力非常重要．某校高一、高二、高三年级分别有学生 1 200 名、 4 5 − 3=a 1=b a b 6 π ( )⋅ +a a b 2a b− ( ) 2⋅ + = + ⋅a a b a a b ( )2 π3 + 3 1 cos 6 = × × 9 2 = ( )22 = 2a b a b− − 2 24 4= ⋅ +a a b b− ( )2 π3 4 3 1 cos +46 = × × ×− 1= 1 080 名、720 名．为了解全校学生的视力情况，学校在 6 月 6 日“全国爱眼日”采用 分层抽样的方法，抽取 50 人测试视力，并根据测试数据绘制了如图所示的频率分布直 方图． （1）求从高一年级抽取的学生人数； （2）试估计该学校学生视力不低于 4.8 的概率； （3）从视力在 内的受测者中随机抽取 2 人，求 2 人视力都在 内的概率． 解：（1）高一年级抽取的学生人数为： ． 答：从高一年级抽取的学生人数为 20． …… 2 分 　　 （2）由频率分布直方图，得 ， 所以 ． …… 4 分 所以抽取 50 名学生中，视力不低于 4.8 的频率为 ， 所以该校学生视力不低于 4.8 的概率的估计值为 ． ……6 分 （3）由频率分布直方图，得 视力在 内的受测者人数为 ，记这 2 人为 ， 视力在 内的受测者人数为 ，记这 3 人为 ． ……8 分 记“抽取 2 人视力都在 内”为事件 A， 从视力在 内的受测者中随机抽取 2 人，所有的等可能基本事件共有 10 个， 分别为 ， 　　　　　 则事件 A 包含其中 3 个基本事件： ， ……10 分 [ )4.0 4.4， [ )4.2 4.4， 120050 201200 1080 720 × =+ + ( )0.2 0.3 1.0 1.5 1.2 0.2 1a+ + + + + × = 0.8a = ( )1.2 0.8 0.2 0.4+ × = 0.4 [ )4.0 4.2， 0.2 0.2 50 2× × = 1 2a a， [ )4.2 4.4， 0.3 0.2 50 3× × = 1 2 3b b b， ， [ )4.2 4.4， [ )4.0 4.4， ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )1 2 1 1 1 2 1 3 2 1 2 2 2 3 1 2a a a b a b a b a b a b a b b b， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ( ) ( )1 3 2 3b b b b， ， ， ( ) ( ) ( )1 2 1 3 2 3b b b b b b， ， ， ， ， （第 18 题） 根据古典概型的概率公式，得 ． 答：2 人视力都在 内的概率为 ． ……12 分 19．（本小题满分 12 分） 如图，在长方体 中，已知 ， ． （1）求证： 平面 ； （2）求二面角 的正切值． 解：（1）因为 为长方体， 所以 平面 ． 　　　 因为 平面 ，所以 ． ……2 分 　　　 因为 ，所以 为正方形． 所以 ． ……4 分 　　　　　 又因为 ， 平面 ， 所以 平面 ． ……6 分 （2）设 ，连接 ． 　　　　　 由（1）知， 平面 ． 因为 平面 ，所以 ． ……8 分 又由（1）知， ， 　　　 所以 为二面角 的平面角． ……10 分 　　　　　 在 中， ， ， 所以 ， 3 10P A =（ ） [ )4.2 4.4， 3 10 1 1 1 1ABCD A B C D− 1AB AD= = 1 2AA = BD ⊥ 1 1A ACC 1A BD A− − 1 1 1 1ABCD A B C D− 1A A ⊥ ABCD BD ⊂ ABCD BD 1A A⊥ AB AD= ABCD BD AC⊥ 1A A AC A= 1A A AC ⊂， 1 1A ACC BD ⊥ 1 1A ACC AC BD O= 1AO BD ⊥ 1 1A ACC 1AO ⊂ 1 1A ACC BD ⊥ 1AO BD AO⊥ 1AOA∠ 1A BD A− − 1Rt A AO△ 1 2AA = 21 2 2AO AC= = 1 1 2tan 2 2 2 2 A AAOA AO ∠ = = = A A1 D1 B1 C1 C B D （第 19 题） A A1 D1 B1 C1 C B D （第 19 题） O 　　　　　 所以二面角 的正切值为 ． ……12 分 20．（本小题满分 12 分） 在锐角△ABC 中，设角 A，B，C 所对的边长分别为 a，b，c，且 ． （1）求 B 的大小； （2）若 AB 2，BC ，点 D 在边 AC 上， ，求 BD 的长． 请在①AD DC；②∠DBC ∠DBA；③BD⊥AC 这三个条件中选择一个，补充在 上面 的横线上，并完成解答． （注：如果选择多个条件分别解答，则按第一个解答计分）． 解：（1）在△ABC 中，由正弦定理 ，及 得， ． …2 分 因为△ABC 为锐角三角形，所以 ，所以 ． 所以 . …… 4 分 又因为 ，所以 . ……6 分 （2）若选①. 法一：在△ABC 中，因为 AD DC，所以 ＝ . …… 8 分 所以 2 ……10 分 所以 BD＝ . ……12 分 法二：在△ABC 中，由余弦定理，得 1A BD A− − 2 2 3sin 2b A a= = 3 2 = = = sin a A = sin b B 3sin 2b A a= 3sin sin sin2B A A= ( )π0 2A∈ ， sin 0A > 3sin 2B = ( )π0 2B∈ ， π 3B = = BD ( )1 2 BA BC+  BD ( )2 21 +24 BA BC BA BC= + ⋅    ( )2 2 3 3 π2 +2 2 cos2 2 3 4 + × × × = 37 16 = 37 4 2 2 2 2 cosAC AB BC AB BC B= + − ⋅ ⋅ ， 所以 ，所以 . …… 8 分 在△ABD 中，由余弦定理，得 即 ， 在△BDC 中，由余弦定理，得 即 . ……10 分 又 ，所以 . 所以 ， 所以 BD＝ . ……12 分 若选②. 在△ABC 中， ， ……8 分 即 ， ……10 分 即 ， 解得 . ……12 分 若选③. 在△ABC 中，由余弦定理，得 ， 所以 . ……8 分 因为 ，又 ， ……10 分 所以 ， ( )2 2 3 3 π2 2 2 cos2 2 3 = + − × × × 13 4 = 13 2AC = 13 4AD DC= = 2 2 2 2 cosAB BD DA BD DA ADB= + − ⋅ ⋅ ∠ 2 13 134 cos16 2BD BD ADB= + − ∠ 2 2 2 2 cosBC BD DC BD DC CDB= + − ⋅ ⋅ ∠ 29 13 13 cos4 16 2BD BD CDB= + − ∠ πADB CDB∠ + ∠ = cos cos 0ADB CDB∠ + ∠ = 29 134 24 8BD+ = + 37 4 ABC ABD CBDS S S= +△ △ △ 1 π 1 π 1 πsin sin sin2 3 2 6 2 6BA BC BA BD BD BC⋅ = ⋅ + ⋅ 31 3 1 1 1 3 12 22 2 2 2 2 2 2 2BD BD× × × = × × × + × × × 6 3 7BD = 2 2 2 2 cosAC AB BC AB BC B= + − ⋅ ⋅ ( )2 2 3 3 π2 2 2 cos2 2 3 = + − × × × 13 4 = 13 2AC = 3 31 sin2 4ABCS BA BC B= ⋅ ⋅ =△ 131 2 4ABCS BD AC BD= ⋅ =△ 13 3 3 4 4BD = 解得 . ……12 分 21．（本小题满分 12 分） 已知圆 C： 关于直线 l： 对称． （1）求实数 a 的值； （2）设直线 m： 与圆 交于点 ，且 ． ① 求 的值； ② 点 P ( 3，0 )，证明：x 轴平分 ． 解：（1）因为圆 C： 关于直线 l： 对称， 　　　　　 所以圆心 C 在直线 l： 上． ……2 分 　　　　　 所以 ，解得 ． …… 4 分 　　 （2）① 由（1）知，圆 C： ． 所以圆心 C 到直线 m： 的距离为 ． ……6 分 因为 ，所以 ，解得 ， 因为 ，所以 ． ……8 分 ② 法一：由①知，直线 m： ． 联立 消去 ，得 ，解得 或 ． 不妨 ， …… 10 分 所以 ． 所以直线 的倾斜角互补，从而 ， 　　 所以 轴平分 ． ……12 分 3 39 13BD = 2 2 2 2 3 0x y x ay+ + − − = 2 1 0x y− + = ( 0 )y kx k= > C A B， 8 5 5AB = k APB∠ 2 2 2 2 3 0x y x ay+ + − − = 2 +1 0x y− = ( )1 a− ， 2 +1 0x y− = 1 2 1 0a− − + = 0a = 2 2( 1) 4x y+ + = ( )1 0− ， 0kx y− = 2 1 k k − + 8 5 5AB = ( )2 2 8 5 2 45 1 k k −= − + 2 4k = 0k > 2k = 2y x= 2 2 2 2 3 0 y x x y x =  + + − = ， ， y 25 2 3 0x x+ − = 1x = − 3 5x = ( ) ( )3 6 1 25 5A B − −， ， ， 6 2 1 15 03 1 3 2 235 PA PBk k −+ = + = − + =− −− PA PB， OPA OPB∠ = ∠ x APB∠ 法二：设直线 m： 上的点 ， ，又点 P ( 3，0 )， 　　　　　 所以 ．（*） ……8 分 　　　　　　 联立 消去 ，得 ， 所以 代入（*），得 ． 所以直线 的倾斜角互补，从而 ， 　　　　　 所以 轴平分 ． ……12 分 22．（本小题满分 12 分） 已 知 函 数 分 别 是 定 义 在 上 的 偶 函 数 和 奇 函 数 ， 且 ． （1）求函数 与 的解析式； 　　（2）设函数 ，若对任意实数 ， 恒成立，求实 数 的取值范围． 解：（1）因为 为偶函数， 为奇函数，且 ，① 所以 ，即 ， ② ……2 分 由①＋② 2 ，得 ， 由①－② 2 ，得 . ……4 分 （2）方法一：由（1）得， ． 2y x= ( )1 12A x x， ( )2 22B x x， 1 2 1 2 2 2 3 3PA PB x xk k x x + = +− − ( ) ( ) ( )( )1 2 2 1 1 2 2 3 2 3 3 3 x x x x x x − + −= − − ( ) ( )( ) 1 2 1 2 1 2 2 2 3 3 3 x x x x x x − +  = − − 2 2 2 2 3 0 y x x y x =  + + − = ， ， y 25 2 3 0x x+ − = 1 2 1 2 2 5 3.5 x x x x  + = −  = − ， 0PA PBk k+ = PA PB， OPA OPB∠ = ∠ x APB∠ ( ) ( )f x g x， R 2( ) ( ) 1f x g x x x+ = − + ( )f x ( )g x ( ) ( ) ( ) 1G x f x a g x= + + x 3( ) 2G x ≥ a ( )f x ( )g x 2( ) ( ) 1f x g x x x+ = − + 2( ) ( ) 1f x g x x x− + − = + + 2( ) ( ) + 1f x g x x x− = + 2( ) 1f x x= + ( )g x x= − ( )G x = ( ) ( ) 1f x a g x+ + 2 1 1x a x= + − + 因为对任意实数 ， 恒成立． 当 时，设 ，则 恒成立. 若 ，即 ，则当 时， 取得最小值 ，符合题意； ……6 分 若 ，即 ，则当 时， 取得最小值 . 由 ，得 ，所以 . 所以 . ……8 分 当 时，设 ，则 恒成立. 若 ，即 ，则当 时， 取得最小值 . 由 ，得 . 所以 . ……10 分 若 ，即 时， ，符合题意. 所以 . 综上，实数 的取值范围是 ． ……12 分 方法二： 恒成立，即 恒成立. 当 时，显然成立； 当 时， ，令 ，设 ， ……6 分 当 ，即 时， . 设 是 上任意两个值，且 ， 则 ， 当 时， ， ， ，所以 ，即 x 3( ) 2G x ≥ 1x≥ ( )2 2 2 1 1( ) 2 2 4 2 a ah x x ax a x a= + − − = + − − − ( )h x 0≥ 12 a− ≤ 2a −≥ 1x = ( )h x 1 2 12 a− > 2a < − 2 ax = − ( )h x 2 1 4 2 a a− − − 2 1 04 2 a a− − − ≥ 2 2 2 2a− − − +≤ ≤ 2 2 2a− − < −≤ 2 2a − −≥ 1x < ( )2 2 2 1 1( ) 2 2 4 2 a ar x x ax a x a= − + − = − − + − ( )r x 0≥ 12 a < 2a < 2 ax = ( )r x 2 1 4 2 a a− + − 2 1 04 2 a a− + − ≥ 2 2 2 2a− +≤ ≤ 2 2 2a− <≤ 12 a ≥ 2a≥ 1( ) (1) 2r x r> = 2 2a −≥ a )2 2 − + ∞ ， 2 3( ) 1 1 2G x x a x= + − + ≥ 211 2a x x− −≥ 1x = 1x ≠ 21 2 1 x a x − −≥ 1x t− = 2 12 2( ) t t h t t + + = − 1x > 0t > ( )2 12 12( ) 22 t t h t tt t + + = − = − + + 1 2t t， (0 )+ ∞， 1 2t t< 1 2( ) ( )h t h t− = ( ) ( ) ( )2 1 1 2 1 2 2 1 2 1 1 2 1 2 1 2 2 11 12 2 ( ) ( )2 2 2 2 t t t tt t t t t tt t t t t t − −− + + + + + = − − = − 1 2 20 2t t< < < 1 22 1t t < 2 1 0t t− > 1 2 0t t > 1 2( ) ( ) 0h t h t− < ； 当 时 ， ， ， ， 所 以 ， 即 ， 所以函数 在 上单调递增，在 上单调递减. ……8 分 所以当 时， 在 上取得最大值 . 所以 . ……10 分 当 ，即 时， ， 同理可证，函数 在 上单调递增，在 上单调递减. 所以当 时， 在 上取得最大值 . 所以 . 综上，实数 的取值范围是 ． …… 12 分 1 2( ) ( )h t h t< 1 2 2 2 t t< < 1 22 1t t > 2 1 0t t− > 1 2 0t t > 1 2( ) ( ) 0h t h t− > 1 2( ) ( )h t h t> ( )h t ( )20 2， ( )2 +2 ∞， 2 2t = ( )h t (0 )+ ∞， 2 2− − 2 2a − −≥ 1x < 0t < 2 12 12( ) 22 t t h t tt t + + = = + + ( )h t ( )2 2 −∞ −， ( )2 02 − ， 2 2t = − ( )h t ( 0)−∞， 2 2− 2 2a −≥ a )2 2 − + ∞ ，