- 2021-05-08 发布 |
- 37.5 KB |
- 12页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013青岛中考数学题(含答案)
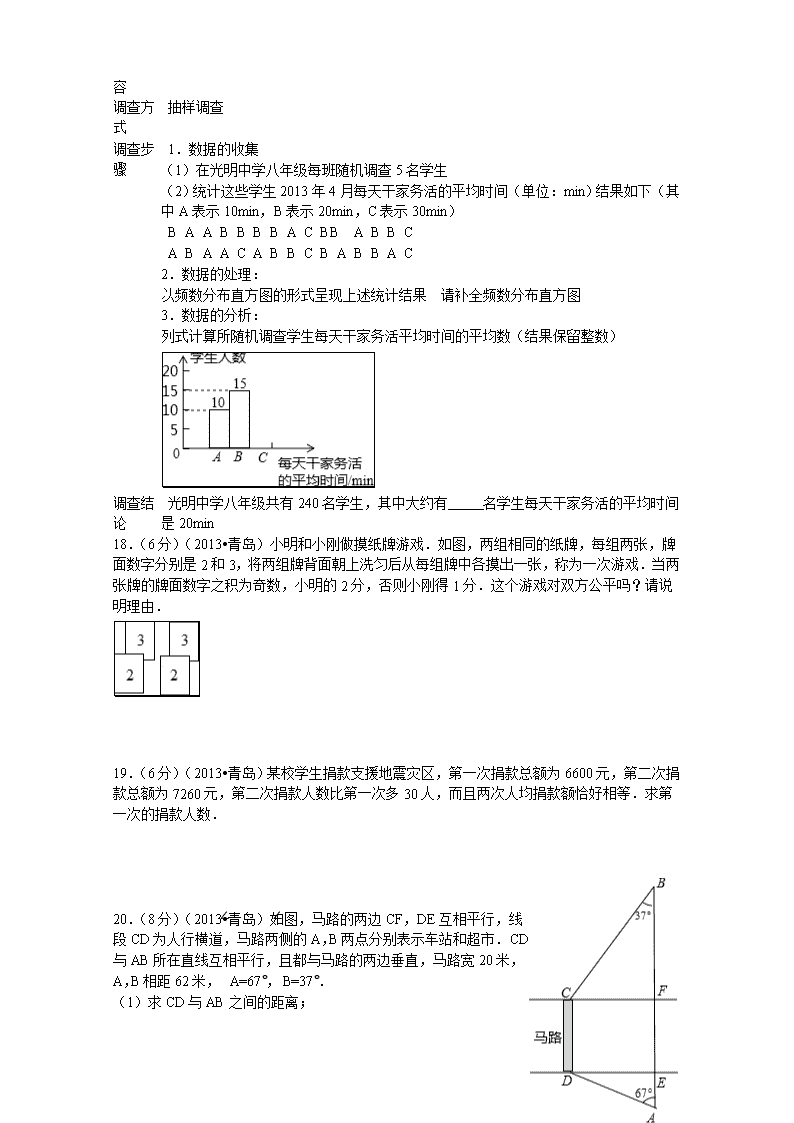
山东省青岛市2013年中考数学试卷 一、选择题(本题满分24分,共有8道小题,每小题3分) 1.(3分)(2013•青岛)﹣6的相反数是( ) A. ﹣6 B. 6 C. ﹣ D. 2.(3分)(2013•青岛)下列四个图形中,是中心对称图形的是( ) A. B. C. D. 3.(3分)(2013•青岛)如图所示的几何体的俯视图是( ) A. B. C. D. 4.(3分)(2013•青岛)“十二五”以来,我国积极推进国家创新体系建设.国家统计局《2012年国民经济和社会发展统计公报》指出:截止2012年底,国内有效专利达8750000件,将8750000件用科学记数法表示为( )件. A. 8.75×104 B. 8.75×105 C. 8.75×106 D. 8.75×107 5.(3分)(2013•青岛)一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:现将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个. A. 45 B. 48 C. 50 D. 55 6.(3分)(2013•青岛)已知矩形的面积为36cm2,相邻的两条边长分别为xcm和ycm,则y与x之间的函数图象大致是( ) A. B. C. D. 7.(3分)直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( ) A. r<6 B. r=6 C. r>6 D. r≥6 8.(3分)(2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( ) A. (,n) B. (m,n) C. (m,) D. () 二、填空题(本题满分18分共有6道题,每小题3分) 9.(3分)(2013•青岛)计算:2﹣1+= . 10.(3分)(2013•青岛)某校对甲、乙两名跳高运动员的近期调高成绩进行统计分析,结果如下:=1.69m,=1.69m,S2甲=0.0006,S2乙=0.00315,则这两名运动员中 的成绩更稳定. 11.(3分)(2013•青岛)某企业2010年底缴税40万元,2012年底缴税48.4万元.设这两年该企业交税的年平均增长率为x,根据题意,可得方程 . 12.(3分)(2013•青岛)如图,一个正比例函数图象与一次函数y=﹣x+1的图象相交于点P,则这个正比例函数的表达式是 . 13.(3分)(2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 . 14.(3分)(2013•青岛)要把一个正方体分割成8个小正方体,至少需要切3刀,因为这8个小正方体都只有三个面是现成的.其他三个面必须用三刀切3次才能切出来.那么,要把一个正方体分割成27个小正方体,至少需用刀切 次;分割成64个小正方体,至少需要用刀切 次. 三、作图题(本题满分4分)用圆规、直尺作图,不写做法,但要保留作图痕迹。 15.(4分)(2013•青岛)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点. 求作:点E,使直线DE∥AB,且点E到B,D两点的距离相等.(在题目的原图中完成作图) 四、解答题(本题满分74分,共有9道小题) 16.(8分)(2013•青岛)(1)解方程组:; (2)化简:(1+)•. 17.(6分)(2013•青岛)请根据所给信息,帮助小颖同学完成她的调查报告 2013年4月光明中学八年级学生每天干家务活平均时间的调查报告 调查目的 了解八年级学生每天干家务活的平均时间 光明中学八年级学生干家务活的平均时间 调查内容 调查方式 抽样调查 调查步骤 1.数据的收集 (1)在光明中学八年级每班随机调查5名学生 (2)统计这些学生2013年4月每天干家务活的平均时间(单位:min)结果如下(其中A表示10min,B表示20min,C表示30min) B A A B B B B A C B B A B B C A B A A C A B B C B A B B A C 2.数据的处理: 以频数分布直方图的形式呈现上述统计结果 请补全频数分布直方图 3.数据的分析: 列式计算所随机调查学生每天干家务活平均时间的平均数(结果保留整数) 调查结论 光明中学八年级共有240名学生,其中大约有 名学生每天干家务活的平均时间是20min 18.(6分)(2013•青岛)小明和小刚做摸纸牌游戏.如图,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上洗匀后从每组牌中各摸出一张,称为一次游戏.当两张牌的牌面数字之积为奇数,小明的2分,否则小刚得1分.这个游戏对双方公平吗?请说明理由. 19.(6分)(2013•青岛)某校学生捐款支援地震灾区,第一次捐款总额为6600元,第二次捐款总额为7260元,第二次捐款人数比第一次多30人,而且两次人均捐款额恰好相等.求第一次的捐款人数. 20.(8分)(2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°. (1)求CD与AB之间的距离; (2)某人从车站A出发,沿折线A→D→C→B去超市B.求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米. (参考数据:sin67°≈,cos67°≈,tan67°≈,sin37°≈,cos37°≈,tan37°≈) 21.(8分)(2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点. (1)求证:△ABM≌△DCM; (2)判断四边形MENF是什么特殊四边形,并证明你的结论; (3)当AD:AB= 时,四边形MENF是正方形(只写结论,不需证明) 22.(10分)(2013•青岛)某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件. (1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式; (2)求销售单价为多少元时,该文具每天的销售利润最大; (3)商场的营销部结合上述情况,提出了A、B两种营销方案: 方案A:该文具的销售单价高于进价且不超过30元; 方案B:每天销售量不少于10件,且每件文具的利润至少为25元 请比较哪种方案的最大利润更高,并说明理由. 23.(10分)(2013•青岛)在前面的学习中,我们通过对同一面积的不同表达和比较,根据图1和图2发现并验证了平方差公式和完全平方公式. 这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化. 【研究速算】 提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法? 几何建模: 用矩形的面积表示两个正数的乘积,以47×43为例: (1)画长为47,宽为43的矩形,如图3,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面. (2)分析:原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021. 用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果. 归纳提炼: 两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述) . 【研究方程】 提出问题:怎样图解一元二次方程x2+2x﹣35=0(x>0)? 几何建模: (1)变形:x(x+2)=35. (2)画四个长为x+2,宽为x的矩形,构造图4 (3)分析:图中的大正方形面积可以有两种不同的表达方式,(x+x+2)2或四个长x+2,宽x的矩形面积之和,加上中间边长为2的小正方形面积. 即(x+x+2)2=4x(x+2)+22 ∵x(x+2)=35 ∴(x+x+2)2=4×35+22 ∴(2x+2)2=144 ∵x>0 ∴x=5 归纳提炼:求关于x的一元二次方程x(x+b)=c(x>0,b>0,c>0)的解. 要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并注明相关线段的长) 【研究不等关系】 提出问题:怎样运用矩形面积表示(y+3)(y+2)与2y+5的大小关系(其中y>0)? 几何建模: (1)画长y+3,宽y+2的矩形,按图5方式分割 (2)变形:2y+5=(y+3)+(y+2) (3)分析:图5中大矩形的面积可以表示为(y+3)(y+2);阴影部分面积可以表示为(y+3)×1,画点部分部分的面积可表示为y+2,由图形的部分与整体的关系可知(y+3)(y+2)>(y+3)+(y+2),即(y+3)(y+2)>2y+5 归纳提炼: 当a>2,b>2时,表示ab与a+b的大小关系. 根据题意,设a=2+m,b=2+n(m>0,n>0),要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图并注明相关线段的长) 24.(12分)(2013•青岛)已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1) 解答下列问题: (1)当t为何值时,四边形AQDM是平行四边形? (2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式: (3)是否存在某一时刻t,使四边形ANPM的面积是平行四边形ABCD的面积的一半?若存在,求出相应的t值;若不存在,说明理由. (4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成的两部分?若存在,求出相应的t值;若不存在,说明理由. 山东省青岛市2013年中考数学试卷 一、选择题(本题满分24分,共有8道小题,每小题3分) 1.B.2.D.3.A.4.C.5.A.6.A.7.C.8.D. 二、填空题(本题满分18分共有6道题,每小题3分) 9.5 10.甲.11.40(1+x)2=48.4.12.k=﹣2 13.﹣ . 14.6;9. 四、解答题(本题满分74分,共有9道小题) 17.解:从图表中可以看出C的学生数是5人, 如图: 每天干家务活平均时间是:(10×10+15×20+5×30)÷30≈18(min); 根据题意得:240×=120(人), 光明中学八年级共有240名学生,其中大约有120名学生每天干家务活的平均时间是20min; 故答案为:120. 18.解:根据题意,画出树状图如下: 一共有4种情况,积是偶数的有3种情况,积是奇数的有1种情况, 所以,P(小明胜)=×2=, P(小刚胜)=×1=, ∵≠, ∴这个游戏对双方不公平. 19.解:设第一次的捐款人数是x人,根据题意得: =, 解得:x=300, 经检验x=300是原方程的解, 20.解:(1)CD与AB之间的距离为x, 则在Rt△BCF和Rt△ADE中, ∵=tan37°,=tan67°, ∴BF==x,AE==x, 又∵AB=62,CD=20, ∴x+x+20=62, 解得:x=24, 答:CD与AB之间的距离为24米; (2)在Rt△BCF和Rt△ADE中, ∵BC===40, AD===26, ∴AD+DC+CB﹣AB=40+20+26﹣62=24(米), 答:他沿折线A→D→C→B到达超市比直接横穿马路多走24米. 21.(1)证明:∵四边形ABCD是矩形, ∴AB=DC,∠A=∠D=90°, ∵M为AD中点, ∴AM=DM, 在△ABM和△DCM, ∴△ABM≌△DCM(SAS); (2)答:四边形MENF是菱形. 证明:∵N、E、F分别是BC、BM、CM的中点, ∴NE∥CM,NE=CM,MF=CM, ∴NE=FM,NE∥FM, ∴四边形MENF是平行四边形, ∵△ABM≌△DCM, ∴BM=CM, ∵E、F分别是BM、CM的中点, ∴ME=MF, ∴平行四边形MENF是菱形; (3)解:当AD:AB=2:1时,四边形MENF是正方形. 理由是:∵M为AD中点, ∴AD=2AM, ∵AD:AB=2:1, ∴AM=AB, ∵∠A=90∴∠ABM=∠AMB=45°, 同理∠DMC=45°, ∴∠EMF=180°﹣45°﹣45°=90°, ∵四边形MENF是菱形, ∴菱形MENF是正方形, 故答案为:2:1. 22.解:(1)由题意得,销售量=250﹣10(x﹣25)=﹣10x+500, 则w=(x﹣20)(﹣10x+500) =﹣10x2+700x﹣10000; (2)w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250. ∵﹣10<0, ∴函数图象开口向下,w有最大值, 当x=35时,wmax=2250, 故当单价为35元时,该文具每天的利润最大; (3)甲方案利润高.理由如下: 甲方案中:20<x≤30, 故当x=30时,w有最大值, 此时w甲=2000; 乙方案中:, 故x的取值范围为:45≤x≤49, ∵函数w=﹣10(x﹣35)2+2250,对称轴为x=35, ∴当x=45时,w有最大值, 此时w乙=1250, ∵w甲>w乙, ∴甲方案利润更高. 23. 归纳提炼: 十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,构成运算结果. 【研究方程】 归纳提炼: 画四个长为x+b,宽为x的矩形,构造答图1,则图中的大正方形面积可以有两种不同的表达方式:(x+x+b)2或四个长为x+b,宽为x的矩形面积之和,加上中间边长为b的小正方形面积. 即:(x+x+b)2=4x(x+b)+b2 ∵x(x+b)=c, ∴(x+x+b)2=4c+b2 ∴(2x+b)2=4c+b2 ∵x>0, ∴x=. 【研究不等关系】 归纳提炼: (1)画长为2+m,宽为2+n的矩形,并按答图2方式分割. (2)变形:a+b=(2+m)+(2+n) (3)分析:图中大矩形面积可表示为(2+m)(2+n),阴影部分面积可表示为2+m与2+n的和.由图形的部分与整体的关系可知,(2+m)(2+n)>(2+m)+(2+n),即ab>a+b. 24 解答: 解:(1)∵当AP=PD时,四边形AQDM是平行四边形, 即3t=3﹣3t, t=, ∴当t=s时,四边形AQDM是平行四边形. (2)∵四边形ABCD是平行四边形, ∴AB∥CD, ∴△AMP∽△DQP, ∴=, ∴=, ∴AM=t, ∵MN⊥BC, ∴∠MNB=90°, ∵∠B=45°, ∴∠BMN=45°=∠B, ∴BN=MN, ∵BM=1+t, 在Rt△BMN中,由勾股定理得:BN=MN=(1+t), ∵四边形ABCD是平行四边形, ∴AD∥BC, ∵MN⊥BC, ∴MN⊥AD, ∴y=×AP×MN =•3t•(1+t) 即y与t之间的函数关系式为y=t2+t(0<t<1). (3)假设存在某一时刻t,四边形ANPM的面积是平行四边形ABCD的面积的一半. 此时t2+t=×3×, 整理得:t2+t﹣1=0, 解得t1=,t2=(舍去) ∴当t=s时,四边形ANPM的面积是平行四边形ABCD的面积的一半. (4)存在某一时刻t,使NP与AC的交点把线段AC分成的两部分, 理由是:假设存在某一时刻t,使NP与AC的交点把线段AC分成的两部分, ∵四边形ABCD是平行四边形, ∴AD∥BC, ∴△APW∽△CNW, ∴=, 即=或=, ∴t=或, ∵两数都在0<t<1范围内,即都符合题意, ∴当t=s或s时,NP与AC的交点把线段AC分成的两部分.查看更多