中考数学三轮真题集训冲刺知识点20二次函数几何方面的应用pdf含解析
1 / 55
一、选择题
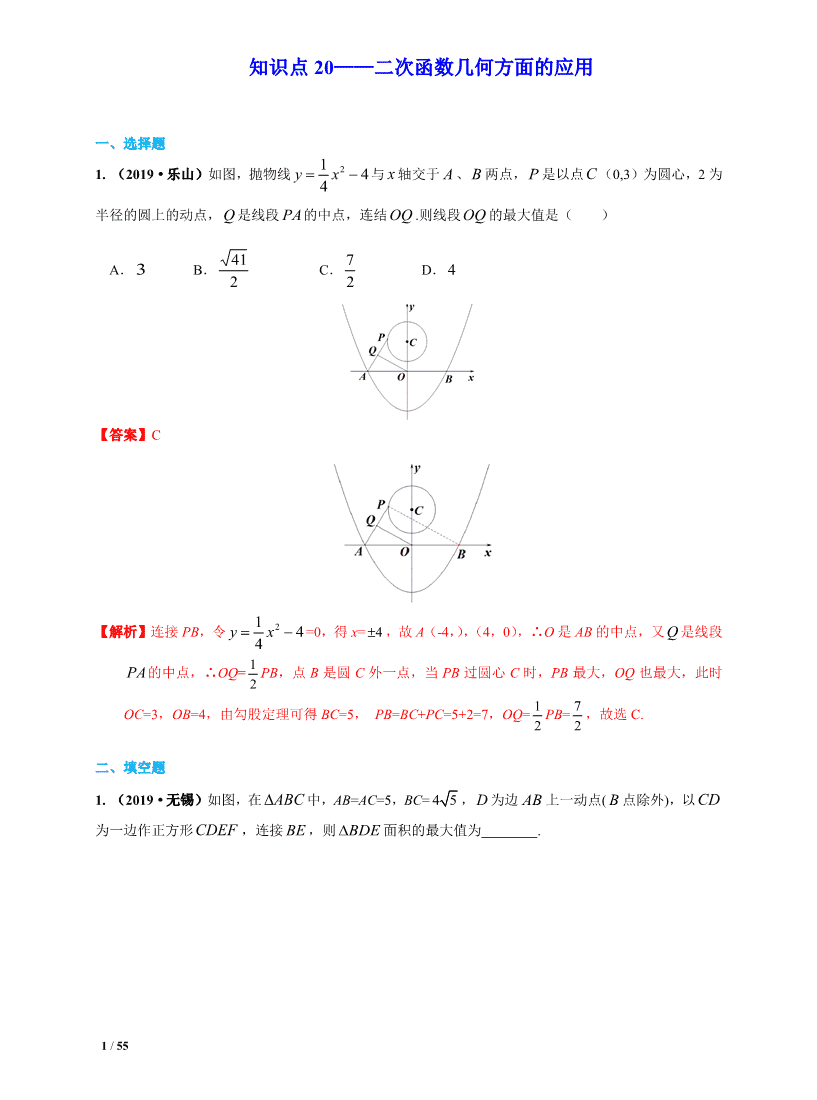
1. (2019·乐山)如图,抛物线 44
1 2 −= xy 与 x 轴交于 A 、B 两点,P 是以点C (0,3)为圆心,2 为
半径的圆上的动点,Q 是线段 PA的中点,连结OQ .则线段OQ 的最大值是( )
A. 3 B.
2
41 C.
2
7 D. 4
【答案】C
【解析】连接 PB,令 44
1 2 −= xy =0,得 x= 4± ,故 A(-4,),( 4,0), ∴ O 是 AB 的中点,又Q 是线段
PA的中点,∴OQ= 1
2
PB,点 B 是圆 C 外一点,当 PB 过圆心 C 时,PB 最大,OQ 也最大,此时
OC=3,OB=4,由勾股定理可得 BC=5, PB=BC+PC=5+2=7,OQ= 1
2
PB= 7
2
,故选 C.
二、填空题
1. (2019·无锡)如图,在 ABC∆ 中,AB=AC=5,BC= 45,D 为边 AB 上一动点( B 点除外),以 CD
为一边作正方形CDEF ,连接 BE ,则 BDE∆ 面积的最大值为 .
知识点 20——二次函数几何方面的应用
2 / 55
【答案】8
【解析】过 D 作 DG⊥BC 于 G,过 A 作 AN⊥BC 于 N,过 E 作 EH⊥HG 于 H,延长 ED 交 BC 于 M.易
证△EHD≌△DGC,可设 DG=HE=x,∵AB=AC=5,BC= 45,AN⊥BC,∴BN= 1
2
BC=2 5 ,AN=
225AB BN−=,∵ G⊥BC,AN⊥BC,∴ DG∥AN,∴ 2BG BN
DG AN
= = ,∴BG=2x,CG=HD=4 5 - 2x;
易证△HED∽△GMD,于是 HE HD
GM GD
= , 45 2xx
GM x
−= ,即 MG
2
45 2
x
x
=
− ,所以 S△BDE = 1
2
BM
×HD= 1
2
×(2x
2
45 2
x
x
−
−
)×(4 5 - 2x)= 25 452 xx−+ =
2
5 45 825x
−− +
,当 x= 45
5
时,S△BDE
的最大值为 8.
2. (2019· 台州)如图,直线 l1∥l2∥l3,A,B,C 分别为直线 l1,l2,l3 上的动点,连接 AB,BC,AC,线段 AC 交直线
l2 于点 D.设直线 l1,l2 之间的距离为 m,直线 l2,l3 之间的距离为 n,若∠ABC=90°,BD=4,且 2
3
m
n
= ,则 m+n
的最大值为________.
3 / 55
【答案】 25
3
【解析】过点 B 作 BE⊥l1 于点 E,作 BF⊥l3 于点 F,过点 A 作 AN⊥l2 于点 N,过点 C 作 CM⊥l2 于点 M,设
AE=x,CF=y,则 BN=x,BM=y,∵BD=4,∴DM=y-4,DN=4-x,∵∠ABC=90°,且∠AEB=∠BFC=
90°,∠CMD=∠AND=90°,易得△AEB∽△BFC,△CMD∽△AND,∴ AE BE
BF CF
= ,即 xm
ny
= ,mn=xy,∴
AN DN
CM DM
= ,即 42=43
mx
ny
−= − ,∴y=10- 3
2 x ,∵ 2= 3
m
n ,∴n= 3
2 m,m+n= 5
2 m,∵mn=xy=x(10- 3
2 x )=-
3
2 x2+10x= 3
2 m2,当 x=10
3 时,mn 取得最大值为 50
3 ,∴ 3
2 m2= 50
3 ,∴m 最大=10
3 ,∴m+n= 5
2 m= 25
3 .
3. (2019·凉山)如图,正方形 ABCD 中,AB=12, AE =
4
1 AB,点 P 在 BC 上运动 (不与 B、C 重 合 ),
过点 P 作 PQ⊥EP,交 CD 于点 Q,则 CQ 的最大值为 .
【答案】4
【解析】在正方形 ABCD 中,∵AB=12, AE =
4
1 AB=3,∴BC=AB=12,BE=9,设 BP=x,则 CP=12-x.∵
PQ⊥EP,∴ ∠ EPQ=∠B=∠C=90°,∴∠BEP+∠BPE=∠CPQ+∠BPE=90° ,∴ ∠ BEP=∠CPQ,∴ △ EBP
∽△PCQ,∴
BE
PC
BP
CQ = ,∴
9
12 x
x
CQ −= ,整理得 CQ= 4)6(9
1 2 +−− x ,∴当 x=6 时,CQ 取得最大
值为 4.故答案为 4.
4 / 55
三、解答题
1.(2019 山东烟台,25,13 分)
如图,顶点为 M 的抛物线 y = ax2 + bx + 3与 x 轴交于 A(−1,0) , B 两点,与 y 轴交于点 C,过点
C 作CD ⊥ y 轴交抛物线与另一个点 D,作 DE ⊥ x 轴,垂足为点 E.双曲线 y 6 (x 0)x
= > 经过点
D,连接 MD,BD.
(1)求抛物线的解析式.
(2)点 N,F 分别是 x 轴,y 轴上的两点,当 M,D,N,F 为顶点的四边形周长最小时,求出点 N,
F 的坐标;
(3)动点 P 从点 O 出发,以每秒 1 个单位长度的速度沿 OC 方向运动,运动时间为 t 秒,当 t 为何值
时, BPD∠ 的度数最大?(请直接写出结果)
【解题过程】
(1)当 0x = 时 20 033ya b=× +×+=
所以 3OC = , (0,3)C ,
因为CD y⊥ 轴, DE x⊥ 轴,CO EO⊥ ,
所以四边形 OEDC 为矩形,
又因为双曲线 6 ( 0)yxx
= > 经过点 D,
所以 6OEDCS =矩形 ,
5 / 55
所以 2OEDCSCD OC
= =矩形 ,
所以 (2,3)D
将点 ( 1, 0)A − 、 (2,3)D 代入抛物线 2 3y ax bx= ++得
30
4 2 33
ab
ab
−+=
+ +=
解得 1
2
a
b
= −
=
所以抛物线的表达式为 2 23yx x=−+ +.
(2)解:作点 D 关于 x 轴的对称点 H ,作点 M 关于 y 轴的对称点 I ,如图(1)
由图形轴对称的性质可知 FM FI= , ND NH= ,
所以四边形 MDNF 的周长 MD DN FN FM MD NH FN FI= +++ = + ++,
因为 MD 是定值,所以当 NH FN FI++最小时,四边形 MDNF 的周长最小,
因为两点之间线段最短,所以当 I、F、N、H 在同一条直线上时 NH FN FI++最小
所以当 I、F、N、H 在同一条直线上时,四边形 MDNF 的周长最小,
连接 HI ,交 x 轴于点 N,交 y 轴于点 F,
因为抛物线的表达式为 2 23yx x=−+ +,所以点 M 的坐标为 (1, 4) ,
由轴对称的性质可得, ( 1, 4)I − , (2, 3)H − ,
设直线 HI 的表达式为 y mx n= + ,
所以 4
23
mn
mn
−+=
+=−
,
第 1题答图(1)
6 / 55
解得
7
3
5
3
m
n
= −
=
,
所以直线 HI 的表达式为 75
33yx=−+,
当 0x = 时, 5
3y = ,
当 0y = 时, 750 33x=−+,所以 5
7x = ,
所以 5(0, )3F , 5( ,0)7N ,
所以当 M,D,N,F 为顶点的四边形周长最小时, 5(0, )3F , 5( ,0)7N .
(3)解:本题的答案为9 2 15− .
解题分析:如图(2),当两点 A、B 距离是定值,直线 CD 是一条固定的直线,点 P 在
直线 CD 上移动,由下图可以看出只有当过 A、B 的圆与直线 CD 相切时 APB∠ 最大.
所以可作 T 过点 B、D,且与直线 OC 相切,切点为 P,此时 BPD∠ 的度数最大,
由已知,可得OP t= , (0, )Pt
因为直线 OC 与 T 相切,
所以TP OC⊥ ,
所以直线 PT 的解析式为 yt=
因为抛物线的表达式为 2 23yx x=−+ +,
第 1题答图(2) 第 1题答图(3)
7 / 55
所以点 B 的坐标为 (3, 0) ,
因为点 B(3, 0) 、点 (2,3)D
可以求得直线 BD 的垂直平分线的解析式为 12
33yx= +
联立 yt= 与 12y =
3 x +
3
,得 x = 3t − 2 , y = t
直线 PT 与直线 BD 的交点即为点 M,所以 M (3t − 2,t)
因为 MB = MC ,可得3t − 2 = (3t − 2 −3)2 + (t − 0)2
解得t = 9 − 2 15 或t = 9 + 2 15 (舍去)
所以当t = 9 − 2 15 时,∠BPD 的度数最大.
2.(2019 江苏盐城卷,27,14)如图所示,二次函数 y = k(x −1)2 + 2 的图象与一次函数 y = kx − k + 2 的
图象交于 A , B 两点,点 B 在点 A 的右侧,直线 AB 分别于 x 轴、 y 轴交于C 、 D 两点,且 k < 0 .
(1)求 A , B 两点横坐标;
(2)若△OAB 是以OA为腰的等腰三角形,求 k 的值;
(3)二次函数图象的对称轴与 x 轴交于点 E ,是否存在实数 k ,使得 ∠ODC = 2∠BEC ,若存在,求出 k
的值;若不存在,说明理由.
【解题过程】(1)∵A、B 是 与 的交点
y
x
D
CB
A
O
2( 1) 2y kx= −+ 2y kx k= −+
8 / 55
, ,
∵ 点在 点的右侧 , 点横坐标是 , 点横坐标 .
(2)由(1)可知 和
∵
由两点间距离公式可得:
∵△OAB 是以 为腰的等腰三角形
分为两种情况: 或
当 时即
∵
当 时即 或
综上所述, 或 或 .
(3)存在, 或
【提示】由(1)可知 和 .根据题意分为两种情况:点 在点 左侧,点 在点 右侧.
当点 在点 左侧时
如图 1,过点 作 轴于点 ,作 的垂直平分线交 轴于点 ,连接
∵
设 =m ,由(1)可知 和 .
在 Rt△BFH 中,由 得
∵
∵ ,
∵
∴
2( 1) 2
2
y kx
y kx k
= −+
= −+
∴ 2( 1) 2= ( 1) 2kx kx− + −+ ∴ ( 1)( 2) 0kx x− −=
∴ 1 1x = 2 2x = ∴ 1
1
=1
2
x
y
=
2
2
=2
2+
x
yk
=
B A ∴ (1, 2)A (2, 2+k)B ∴ A 1 B 2
(1, 2)A (2, 2+k)B
(0,0)O
∴ 22= 5, 4 ( 2) , 1OA OB k AB k= ++ = +
OA
∴ =OA AB =OA OB
=OA AB 25= 1k + ∴ 2 4k = ∴ 2k = ±
0k < ∴ 2k = −
=OA OB 25 4 ( 2)k= ++ ∴ 2( 2) 1k += ∴ 1k = − 3k = −
∴ 1k = − 2k = − 3k = −
3k = − 47
3k −−=
(1, 2)A (2, 2+k)B B C B C
B C ∴ 2+k>0 ∴ 0>k>-2
B BH x⊥ H BE x F BF
=BF EF ∴ 2BFH BEC∠=∠
=BF EF (1, 2)A (2, 2+k)B ∴ (1, 0)E (2,0)H ∴ 1EH =
∴ 1FH m= −
2 22=BH FH BF+ 2 22( 2) (1 )k mm+ +− =
∴
2 45
2
kkm ++= ∴
2 43=1 2
kkFH m −− −−= ∴ 2
42tan 43
BH kBFH FH k k
+∠==−− −
2ODC BEC∠=∠ ∴ =ODC BFH∠∠ ∴ tan tanODC BFH∠=∠
2(1,1 )C k
− ∴ 2=1OC k
− =2OD k−
∴
21 1tan 2
OC kODC OD k k
−
∠===−−
∴ 2
1 42
43
k
kk k
+−=−− − ∴ 3k = ±
0k < ∴ 3k = −
9 / 55
当点 在点 右侧时
如图,过点 作 轴于点 ,作 的垂直平分线交 轴于点 ,连接
∵
由(1)可知 和 .
设
在 Rt△BMN 中,由 得
∵
∵
∵ ,
∵
图1
x
y
F H
D
CB
A
O E
B C ∴ 2+k<0 ∴ k<-2
B BM x⊥ M BE x N BN
=BN EN ∴ 2BNM BEC∠=∠
(1, 2)A (2, 2+k)B ∴ (1, 0)E (2,0)M ∴ 1EM =
= =nBN EN ∴ 1MN n= −
222BN MN BM= + 2 22( 2) (1 )nk n= + +−
∴
2 45
2
kkn ++= ∴
2 43MN=1 2
kkn −− −−=
= ( 2)BM k−+∴ 2
42tan +4 +3
BM kBNM MN k k
+∠==
2ODC BEC∠=∠ ∴ =ODC BNM∠∠ ∴ tan tanODC BNM∠=∠
2(1,1 )C k
− ∴ 2=1OC k
− =2OD k−
∴
21 1tan 2
OC kODC OD k k
−
∠===−−
∴ 2
1 42
+4 +3
k
kk k
+−= ∴ 23 8 30kk+ +=
∴ 47
3k −±= 2k <− ∴ 47
3k −−=
10 / 55
综上所述, 或 .
3.(2019 江西省,23,12 分)特例感知
(1)如图 1,对于抛物线 y1 = −x2 − x +1, y2 = −x2 − 2x +1, y3 = −x2 −3x +1下列结论正确的序号
是 ;
①抛物线 1y , 2y , 3y 都经过点 C(0,1);
②抛物线 2y , 3y 的对称轴由抛物线 1y 的对称轴依次向左平移
2
1 个单位得到;
③抛物线 1y , 2y , 3y 与直线 y=1 的交点中,相邻两点之间的距离相等.
形成概念
(2)把满足 12 +−−= nxxyn (n 为正整数)的抛物线称为“系列平移抛物线”.
知识应用
在(2)中,如图 2.
图2
y
xN
M
D
C
B
A
O E
3k = − 47
3k −−=
11 / 55
①“系列平移抛物线”的顶点依次为 1P , 2P , 3P ,…, nP ,用含 n 的代数式表示顶点 nP 的坐标,并
写出该顶点纵坐标 y 与横坐标 x 之间的关系式;
②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”: 1C , 2C , 3C ,…, nC ,其
横坐标分别为-k-1,-k-2,-k-3,…,-k-n(k 为正整数),判断相邻两点之间的距离是否都相等,若相
等,直接写出相邻两点之间的距离;若不相等,说明理由;
③在②中,直线 y=1 分别交“系列平移抛物线”于点 1A , 2A , 3A ,…, nA ,连接 nn AC ,
11 −− nn AC ,判断 nn AC , 11 −− nn AC 是否平行?并说明理由.
【解题过程】解:(1)对于抛物线 12
1 +−−= xxy , 122
2 +−−= xxy , 132
3 +−−= xxy 来说,
∵抛物线 1y , 2y , 3y 都经过点 C(0,1),∴①正确;
∵抛物线 1y , 2y , 3y 的对称轴分别为:
2
1
)1(2
1
1 −=−×
−−=x , 1)1(2
2
2 −=−×
−−=x ,
2
3
)1(2
3
3 −=−×
−−=x 的
∴抛物线 2y , 3y 的对称轴由抛物线 1y 的对称轴依次向左平移
2
1 个单位得到,∴②正确;
∵抛物线 1y , 2y , 3y 与直线 y=1 的另一个交点的横坐标分别为:-1、-2、-3,
∴抛物线 1y , 2y , 3y 与直线 y=1 的交点中,相邻两点之间的距离相等.∴③正确.
答案:①②③
(2)①由 12 +−−= nxxyn 可知,顶点坐标为 nP (
2
n− ,
4
42 +n ),
∴该顶点纵坐标 y 与横坐标 x 之间的关系式为 14
4)2(
4
4 2
22
+=+−=+= xxny ;
12 / 55
②当横坐标分别为-k-1,-k-2,-k-3,…,-k-n(k 为正整数),对应的纵坐标为: 12 +−− kk ,
122 +−− kk , 132 +−− kk ,…, 12 +−− nkk ,
∴ 1C 2C 2222 )]12()1[()]2()1[( +−−−+−−+−−−−−= kkkkkk
2222 )121()21( −+++−−+++−−= kkkkkk
21 k+= ,
2C 3C 2222 )]13()12[()]3()2[( +−−−+−−+−−−−−= kkkkkk
2222 )1312()32( −+++−−+++−−= kkkkkk
21 k+= ,
…,
1−nC nC 2222 )}1(]1)1({[)}()]1({[ +−−−+−−−+−−−−−−= nkkknknknk
2222 ]11)1([)1( −+++−−−++++−−= nkkknknknk
21 k+= ,
∴相邻两点的距离相等,且距离为: 21 k+ .
③将 y=1 代入 12 +−−= nxxyn 可得 112 =+−− nxx ,∴x=-n(0 舍去),
∴点 1A (-1,1), 2A (-2,1), 3A (-3,1),…, nA (-n,1).
∵当横坐标分别为-k-1,-k-2,-k-3,…,-k-n(k 为正整数),对应的纵坐标为: 12 +−− kk ,
122 +−− kk , 132 +−− kk ,…, 12 +−− nkk ,
∴点 1C (-k-1, 12 +−− kk ), 2C (-k-2, 122 +−− kk ), 3C (-k-3, 132 +−− kk ),…, nC (-k-
n, 12 +−− nkk ).
设 nn AC , 11 −− nn AC 的解析式分别为:y=px+q,y=mx+n,
则
+−−=+−−
=+−
1)(
1
2 nkkqpnk
qnp ,
+−−−=+−−−
=+−−
1)1()]1([
1)1(
2 knknmnk
nmn ,
13 / 55
解得 p=k+n,m=k+n-1,
∴p≠m
∴Cn An ,Cn−1An−1 不平行.
4.(2019·山西)综合与探究
如图,抛物线 y=ax2+bx+6 经过点 A(-2,0),B(4,0)两点,与 y 轴交于点 C.点 D 是抛物线上一个动点,设点
D 的横坐标为 m(1
,所以重叠部分不是五边形;当 S= 53时,
23 t +8 32
− =53,此时 t= 62> ,所以重叠部分不是五边形;当 20,∵a>0,
∴b<0;
(2)①过点 D 作 DM⊥y 轴于 M,则 DM∥AO,∴ 1
2
DC DM MC
CA OA CO
= = = , ∴ DM = 1
2
AO,设 A
(-2m,0)(m>0),
则 AO=2m,DM=m.∵OC=4,∴CM=2,∴D(m,-6), B(4m,0),设对称轴交 x 轴于 N,则 DN∥
y 轴,∴ △DNB∽
△
EOB,
∴ DN BN
OE OB
= ,∴OE=8,S△BEF = 1
2
×4×4m =8,∴ m =1,∴A(-2,0), B(4,0),
设 y = a(x + 2)(x - 4),即 y= ax 2-2ax- 8a,令 x=0,则 y=-8a,∴C(0,-8a), ∴ -8a=-4,a= 1
2
,∴ y
= 1
2
x2- x -4.
②易知:B(4m,0), C(0,-4), D(m,-6),由勾股定理得 CB2 =16m2 +16,CD2 = m 2 +4,DB2 =
9m2 + 36.
∵9m 2 +36+16m2 +16> m2 +4,∴CB2 + DB2>CD2,∴∠CB D 为锐角,故同时考虑一下两种情况:
1°当∠CDB 为锐角时,CD2 + DB2>CB2,m2 +4 + 9m 2 +36>16m2 +16 ,解得 -2<m<2,
2°当∠BCD 为锐角时,CD2 +CB 2>DB 2, m2 +4 +16m2 +16> 9m 2 +36,解得 m> 2 或 m<- 2
(舍),
x
y
O
x
y
O
43 / 55
综上: 2 <m<2 ,∴2 2 <2m<4,∴ 2 2 <OA<4.
第 2 1题答图
【知识点】二次函数图像与性质;勾股定理;相似三角形判定与性质;锐角三角形的判定;数形结合思
想
33yx x= + 的图象上,22.(2019·岳阳)如图 1,△AOB 的三个顶点 A、O、B 分别落在抛物线 F1: 1 2
7点 A 的横坐标为-4,点 B 的纵坐标为-2.( 点 A 在点 B 的左侧)
(1)求点 A、B 的坐标;
(2)将△AOB 绕点 O 逆时针转 90°得到△A′OB′,抛物线 F2: 2 4y ax bx= ++经过 A′、B′两
点,已知点 M 为抛物线 F2 的对称轴上一定点,且点 A′恰好在以 OM 为直径的圆上,连接 OM、A′M,
求△OA′M 的面积;
(3)如图 2,延长 OB′交抛物线 F2 于点 C,连接 A′C,在坐标轴上是否存在点 D,使得以 A、O、D
为顶点的三角形与△OA′C 相似.若存在,请求出点 D 的坐标;若不存在,请说明理由.
【思路分析】(1)分别将 A 点横坐标和 B 点纵坐标代入抛物线 F1 可得;(2)通过 A′、B′的坐标求
出抛物线 F2 的函数关系式,根据点 M 在对称轴上求出点 M 的横坐标;延长 A′M 交 x 轴于点 N,则
44 / 55
△A′MN 为等腰直角三角形,求出 N 点坐标,进一步求出直线 A′N 的解析式,得到点 M 的坐标,最
后利用 SA′OM= SA′′ON-SOMN
求解.(3)根据点在直线 OB′和抛物线 F2 上求出点 C 的坐标,得到 A′C 的长度及∠OA′C 的度数,
根据两边成比例并且夹角相等证明三角形相似,分两种情况讨论求点 D 的坐标.
【解题过程】(1)将 x=-4 代入 217
33yx x= + ,得: 217( 4) ( 4) 433y = ×− + ×− =− ,
∴A(-4,-4).
将 y=-2 代入 217
33yx x= + ,得: 217 233xx+=−,
解得:x1=-1,x2=-6
∵点 A 在点 B 的左侧,
∴B(-1,-2)·
(2)由旋转可知:A′(4,-4), B′(2,-1)
代入抛物线 2 4y ax bx= ++,得:
16 4 4 4
424 1
ab
ab
+ +=
+ +=−
解得:
1
4
3
a
b
=
= −
∴抛物线 F2: 21 344yxx= −+.
对称轴为: 3 612 4
x −=−=
×
延长 A′M 交 x 轴于点 N,
∵点 A′恰好在以 OM 为直径的圆上,
∴∠OA′M=90°.
45 / 55
∵A′(4,-4),
∴∠A′ON=45º.
∴△ A′ON 为等腰直角三角形.
∴ON=4×2=8.
∴N(8,0)
设直线 A′N:y=mx+n
则 44
80
mn
mn
+=−
+=
解得: 1
8
m
n
=
= −
∴y=x-8.
当 x=6 时,y=-2.
∴M(6,-2)
∴SA′OM= SA′′ON-SOMN
= 1184 8222
××− ××
=8.
所以,△OA′M 的面积为 8.
(3)设直线 OB′解析式为:y=kx,代入 B′(2,-1),
得:2k=-1
1
2k = − .
设直线 OB′解析式为: 1
2yx= − .
解方程组:
21 344
1
2
yxx
yx
= −+
= −
得: 1
1
2
1
x
y
=
= −
, 2
2
8
4
x
y
=
= −
∵B′(2,-1)
∴C(8,-4).
∵A(4,-4),
∴A′C∥x 轴,A′C=8-4=4,
∴∠OA′C=135º.
若以 A、O、D 为顶点的三角形与△OA′C 相似则△AOD 必有一个钝角 135°,故点 O 与点 A′是对应
顶点.
所以点 D 在 x 轴或 y 轴正半轴上.
46 / 55
OA=OA′= 224 4 42+= .
①若△AOD∽△OA′C,则
''
OA OD
AO AC
=
∴OD=A′C=4.
此时点 D 的坐标为(4,0)或(0,4).
②若△AOD∽△CA′O,则
'C '
OA OD
A AO
=
42
4 42
OD=
∴OD=8.
此时点 D 的坐标为(8,0)或(0,8).
由①②可知,坐标轴上存在点 D,其坐标分别为(4,0)、( 0,4)、( 8,0)或(0,8).
【知识点】二次函数综合,图形的旋转,求二次函数解析式,相似三角形的判定,存在性问题,分类讨
论思想
23. (2019·怀化)如图,在直角坐标系中有 Rt�AOB,O 为坐标原点,OB=1,tan�ABO=3,将此三角
形绕原点 O 顺时针旋转 90°,得到 Rt�COD,二次函数 y=-x2+bx+c 的图象刚好经过 A,B,C 三点.
(1)求二次函数的解析式及顶点 P 的坐标;
(2)过定点 Q 的直线 l:y=kx-k+3 与二次函数图象相交于 M,N 两点.
�若 S�PMN=2,求 k 的值;
�证明:无论 k 为何值,�PMN 恒为直角三角形
�当直线 l 绕着定点 Q 旋转时,�PMN 外接圆圆心在一条抛物线上运动,直接写出抛物线的表达式.
【思路分析】(1)根据题意分别求出点 A 和点 C 的坐标,并把坐标代入 y=-x2+bx+c,解出 b 和 c 的值即
可,进而得出顶点 P 的坐标;
(2)①设 M(x1,y1), N(x2,y2),首先求出定点 Q 的坐标,然后根据 S�PMN= 1
2
PQ·(x2-x1)得出 x1 和
x2 的数量关系,最后联立方程 y=-x2+2x+3 与方程 y=kx-k+3,根据根与系数的关系得出 x1+x2=2-k,x1·x2=-
47 / 55
k,进而求出 k 的值;
②过点 P 作 PG⊥x 轴,垂足为 G,分别过点 M、N 作 PG 的垂线,垂足分别为 E、F,首先表示出线段
PE,ME,
PF,NF,然后根据锐角三角函数的定义得出 tan∠PAE 与 tan∠FPN,根据 x1+x2=2-k,x1·x2=-k,可得 1-
x1=
2
1
1x −
,进而推出 tan∠PAE=tan∠FPN,进而证明出结论;
③设线段 MN 的中点(x,y),由②可得 MN 的中点为( 2
2
k− ,
2 6
2
k−+)进而得出抛物线方程.
【解题过程】(1)解:�OB=1,tan�ABO=3,
�OA=OBtan�ABO=3,
�A(0,3).
根据旋转的性质可得 Rt�AOB�Rt�COD,
�OC=OA=3,
�C(3,0),
根据题意可得 c=3
93 0bc
−+ + =
,解得 2
3
b
c
=
=
,
�二次函数的解析式为 y=-x2+2x+3,顶点坐标 P(1,4)
(2)�解:由直线 l 的方程 y=kx-k+3 可得定点 Q(1,3),
设 M(x1,y1), N(x2,y2), 则
S�PMN= 1
2
PQ·(x2-x1)=2,
�x2-x1=4.
联立 y=-x2+2x+3 与 y=kx-k+3 可得 x2+(k-2)x-k=0,
∴x1+x2=2-k,x1·x2=-k,
∴(x2-x1)2=(x1+x2)2-4x1·x2=k2+4=16,
∴k=± 23.
②证明:过点 P 作 PG⊥x 轴,垂足为 G,分别过点 M、N 作 PG 的垂线,垂足分别为 E、F.
设 M(x1,y1), N(x2,y2).
48 / 55
∵M,N 在二次函数 y=-x2+2x+3 图象上,
∴y1=-x12+2x1+3,y2=-x22+2x2+3.
∵P(1,4),
∴PE=4-y1=4+x12-2x1-3=(x1-1)2,ME=1-x1,
PF=4-y2=4+x22-2x2-3=(x2-1)2,NF=x2-1,
∴tan∠PAE=
( )2
1
1
1
1=11
xPE xME x
− = −−
,
tan∠FPN= ( )
2
2
22
1 1
11
xFN
PF xx
−= = −−
.
由①可知 x1+x2=2-k,x1·x2=-k,
∴x1+x2=2+x1x2,
∴(1-x1)(x2-1)=1,
∴1-x1=
2
1
1x −
,
∴tan∠PAE=tan∠FPN,
∴∠PAE=∠FPN.
∵∠PAE+∠APE=90°,
∴∠FPN+∠APE=90°,
即∠APN=90°,
∴无论 k 为何值,�PMN 恒为直角三角形.
③解:设线段 MN 的中点(x,y),
由②可得 MN 的中点为( 2
2
k− ,
2 6
2
k−+),
∴ 2
2
2
6
2
kx
ky
− = −+ =
,化简,得 y=-2x2+4x+1.
∴抛物线的表达式为 y=-2x2+4x+1.
【知识点】待定系数法求二次函数的解析式,一次函数与二次函数的交点问题,锐角三角函数的定义,
一元二次方程根与系数的关系,中点坐标公式
24.(2019 山东省德州市,25,14)如图,抛物线 y=mx2﹣ mx﹣4 与 x 轴交于 A(x1,0),B(x2,0)
两点,与 y 轴交于点 C,且 x2﹣x1= .
(1)求抛物线的解析式;
49 / 55
(2)若 P(x1,y1), Q(x2,y2)是抛物线上的两点,当 a≤x1≤a+2,x2≥ 时,均有 y1≤y2,求 a
的取值范围;
(3)抛物线上一点 D(1,﹣5), 直 线 BD 与 y 轴交于点 E,动点 M 在线段 BD 上,当∠BDC=∠
MCE 时,求点 M 的坐标.
【思路分析】(1)函数的对称轴为:x=﹣ = = ,而且 x2﹣x1= ,将上述两式联立并
解得:x1=﹣ ,x2=4,从而求出抛物线的解析式;
(2)由(1)知,函数的对称轴为:x= ,则 x= 和 x=﹣2 关于对称轴对称,故其函数值相等,
结合函数图象求出 a 的取值范围;
(3)确定△BOC、△CDG 均为等腰直角三角形来求解.
【解题过程】解 :( 1)函数的对称轴为:x=﹣ = = ,而且 x2﹣x1= ,
将上述两式联立并解得:x1=﹣ ,x2=4,
则函数的表达式为:y=a(x+ )( x﹣4)=a(x2﹣4x+ x﹣6),
即:﹣6a=﹣4,解得:a= ,
故抛物线的表达式为:y= x2﹣ x﹣4;
(2)由(1)知,函数的对称轴为:x= ,
则 x= 和 x=﹣2 关于对称轴对称,故其函数值相等,
50 / 55
又 a≤x1≤a+2,x2≥ 时,均有 y1≤y2,
结合函数图象可得: ,解得:﹣2≤a≤ ;
(3)如图,连接 BC、CM,过点 D 作 DG⊥OE 于点 G,
而点 B、C、D 的坐标分别为:(4,0)、( 0,﹣4)、( 1,﹣5),
则 OB=OC=4,CG=GC=1,BC=4 ,CD= ,
故△BOC、△CDG 均为等腰直角三角形,
∴∠BCD=180°﹣∠OCB﹣∠GCD=90°,
在 Rt△BCD 中,tan∠BDC= =4,
∠BDC=∠MCE,
则 tan∠MCE=4,
将点 B、D 坐标代入一次函数表达式:y=mx+n 并解得:
直线 BD 的表达式为:y= x﹣ ,故点 E(0,﹣ ),
设点 M(n, n﹣ ), 过 点 M 作 MF⊥CE 于点 F,
则 MF=n,CF=OF﹣OC= ﹣ ,
tan∠MCE= = =4,
解得:n= ,
51 / 55
故点 M( ,﹣ ).
26.(2019 山东滨州,26,14 分)如图
①
,抛物线 y=- x2+ x+4 与 y 轴交于点 A,与 x 轴交于点 B,
C,将直线 AB 绕点 A 逆时针旋转 90°,所得直线与 x 轴交于点 D.
(1)求直线 AD 的函数解析式;
(2)如图
②
,若点 P 是直线 AD 上方抛物线上的一个动点
①
当点 P 到直线 AD 的距离最大时,求点 P 的坐标和最大距离;
②
当点 P 到直线 AD 的距离为 时,求 sin∠PAD 的值.
【思路分析】(1)根据抛物线 y=- x2+ x+4 与 y 轴交于点 A,与 x 轴交于点 B,C,可以求得点
A、B、C 的坐标,再根据将直线 AB 绕点 A 逆时针旋转 90°,所得直线与 x 轴交于点 D,可以求得
点 D 的坐标.从而可以求得直线 AD 的函数解析式;( 2)
①
根据题意,作出合适的辅助线,然后根
据二次函数的性质即可求得点 P 到直线 AD 的距离最大值,进而可以得到点 P 的坐标;
②
根据
①
中
关系式和题意,可以求得点 P 对应的坐标,从而可以求得 sin∠PAD 的值.
【解题过程】
解 :( 1)当 x=0 时,y=4,则点 A 的坐标为(0,4),………………………………………1 分
当 y=0 时,0=- x2+ x+4,解得 x1=-4,x2=8,
则点 B 的坐标为(-4,0), 点 C 的坐标为(8,0),
∴OA=OB=4,∴∠OBA=∠OAB=45°.
∵将直线 AB 绕点 A 逆时针旋转 90°得到直线 AD,
∴∠BAD=90°,∴OAD=45°,∴∠ODA=45°,∴OA=OD,
∴点 D 的坐标为(4,0).………………………………………………………………………2 分
52 / 55
设直线 AD 的函数解析式为 y=kx+b,
,得 ,
即直线 AD 的函数解析式为 y=-x+4.……………………………………………………………4 分
(2)作 PN⊥x 轴交直线 AD 于点 N,如右图
①
所示,
设点 P 的坐标为(t,- t2+ t+4), 则 点 N 的坐标为(t,-t+4),
∴PN=(- t2+ t+4)-(-t+4)=- t2+ t,………………………………………………6 分
∴PN⊥x 轴,∴PN∥y 轴,∴∠OAD=∠PNH=45°.
作 PH⊥AD 于点 H,则∠PHN=90°,
∴PH= = (- t2+ t)= t=- (t-6)2+ ,
∴当 t=6 时,PH 取得最大值 ,此时点 P 的坐标为(6, ),………………………………8 分
即当点 P 到直线 AD 的距离最大时,点 P 的坐标是(6, ),最大距离是 .………………9 分
②
当点 P 到直线 AD 的距离为 时,如右图
②
所示,
则 t= ,
解得 t1=2,t2=10,………………………………………………………………………10 分
则 P1 的坐标为(2, ), P2 的坐标为(10,- ).
当 P1 的坐标为(2, ), 则 P1A= = ,
∴sin∠P1AD= = ;…………………………………………………………12 分
53 / 55
当 P2 的坐标为(10,- ), 则 P2A= = ,
∴sin∠P2AD= = ;
由上可得,sin∠PAD 的值是 或 .……………………………………………14 分
25. (2019·遂宁)如图,顶点为 P(3,3)的二次函数图像与 x 轴交于点 A(6,0),点 B 在该图像上,
OB 交其对称轴 l 于点 M,点 M,N 关于点 P 对称,连接 BN,ON(1)求该二次函数的关系式;
(1) 若点 B 在对称轴 l 右侧的二次函数图像上运动,请解答下列问题:
①连接 op,当 OP=
MN2
1
时,请判断△NOB 的形状,并求出此时点 B 的坐标;
②求证:∠BNM=∠ONM
【解析】(1)根据顶点为 P(3,3),可以设关系式为顶点式,将点 A(6,0)代入关系式,从而求出二次
函数的关系式;
(2)①∵OP=
MN2
1
,点 M,N 关于点 P 对称∴OP=PM=PN,根据等边对等角可以证明∠BON=90°,从而证
明△NOB 是直角三角形.∵P(3,3)∴OP= 23 =PM,∴M(3,3- 23 )可以求出直线 OM 的解析式,直线与
抛物线交点为 B,从而可求得 B 点坐标.
②∵点 N 在对称轴上,点 O,A 关于对称轴对称,∴ON=NA,∴∠BNM=∠ONM
解 :( 1)∵P(3,3),
∴设二次函数的关系式为 y=a(x-3)2+3,
∵A(6,0)
54 / 55
∴a=
9
1-
∴二次函数的关系式为 y=
9
1- (x-3)2+3;
(2)①∵OP=
MN2
1
,点 M,N 关于点 P 对称
∴OP=PM=PN,
∵OP=PM
∴∠POM=∠OMP;
同理,∠PON=∠ONP;
∵∠POM+∠OMP+∠PON+∠ONP=180°,
∴∠POM+∠NOP=90°
所以△NOB 是直角三角形.
∵P(3,3)
∴OP= 23 =PM,
∴M(3,3- 23 )
∴直线 OM 的解析式为 xy )21( −= ,
∵抛物线的解析式为 y=
9- 1 (x-3)2+3
∴联立方程组可得 x=3-9 2 ,
∴B(3-9 2 , 22-12 2 )
②∵点 N 在对称轴上,点 O,A 关于对称轴对称,
∴ON=NA,
∴∠BNM=∠ONM.
26.(2019·广元)如图,直线 y=-x+4 与 x 轴,y 轴分别交于 A,B 两点,过点 A,B 两点的抛物线 y=ax2+bx+c
与 x 轴交于点 C(-1,0).
(1)求抛物线的解析式;
(2)连接 BC,若点 E 是线段 AC 上一个动点(不与 A,C 重合),过点 E 作 EF∥BC,交 AB 于点 F,当△BEF 的面
积是 5
2
时,求点 E 的坐标;
(3)在(2)的结论下,将△BEF 绕点 F 旋转 180°得△B’E’F,试判断点 E’是否在抛物线上,并说明理由.
55 / 55
解:(1)令 y=-x+4 中 x=0,则 y=4,∴B(0,4),令 y=0,则-x+4=0,x=4,∴A(4,0),又∵C(-1,0),将 A,B,C
代入抛物线得
4
16 4 0
0
c
a bc
abc
ì =ïï + +=íï - +=ïî
,解得
1
3
4
a
b
c
ì =-ïï =íï =ïî
,∴抛物线的解析式为 y=-x2+3x+4;
(2) 连接 OF,设 E(m,0),∵B(0,4),C(-1,0),∴kBC=
( )
40 401
y
x
-==--
,∵EF∥BC,∴kEF=kBC=4,设 lEF:y=
4x+b,∵E(m,0),∴解得 b=-4m,∴lEF:y=4x-4m,联立 y=-x+4,解得
44
55
4 16
55
xm
ym
ì =+ïïíï =- +ïî
,∴F( 44
55m + ,
4 16
55m-+)∴S△BEF=S 四边形 OBFE-S△OEB=S△OEF+S△OBF-S△OEB= 1
2 FOE y× + 1
2 FOB x× - 1
2 OB OE×
= 22 68
5 55mm- ++,∴ 22 6 85
5 5 52mm- + +=,解得 m= 3
2
,
∴E( 3
2
,0);
(3)由(2)知 E( 3
2
,0),∴F(2,2),∵△BEF 绕点 F 旋转 180°得△B’E’F,∴E’与 E 关于点 F 对称,∴E’( 5
2
,4),将
x= 5
2
代入抛物线 y=-x2+3x+4 得 y= 21
4
≠4,∴点 E’不在抛物线上.