- 2021-05-08 发布 |
- 37.5 KB |
- 17页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件八年级下册数学课件《勾股定理的逆定理》 人教新课标 (2)_人教新课标
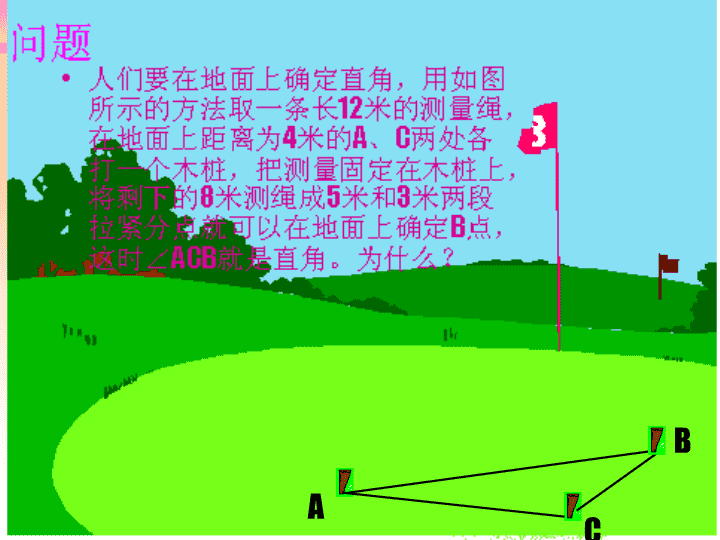
课题:勾股定理的逆 定理 A C B 操作 n 每个同学的桌上有一段12cm长的线,请同学 量出4cm,用大头钉固定好把生下的线分成 5cm和3cm两段拉紧固定,用量角器量出最大 角的度数。 勾股定理的逆命题 n 如果三角形的一条边的平方等于其它两条边 的平方和,那么这个三角形是直角三角形。 n 已知: n 求证: n 证明: c a b B C A 在△ABC中,AB=c BC=a CA=b 且a2+b2=c2 △ ABC是直角三角形 画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b a b A’ B’ C’ ∵ ∠ C’=900 ∴ A’B’2= a2+b2 ∵ a2+b2=c2 ∴ A’B’ 2=c2 ∴ A’B’ =c ∵ 边长取正值 ∴ △ ABC ≌ △ A’B’C’(SSS) ∴ ∠ C= ∠ C’(全等三角 形对应角相等) ∴ ∠C= 900 BC=a=B’C’ CA=b=C’A’ AB=c=A’B’ c a b B C A a b B' C' A' 已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2 求证:△ ABC是直角三角形 证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b 在△ ABC和△ A’B’C’中 ∴ △ ABC是直角三角形(直 角三角形的定义) 如果三角形中两边的平方和等于第三边的 平方,那么这个三角形是直角三角形。 (1)上述结论中,哪条边所对的角是直角? (2)如果三角形中较短两边的平方和不等于 最长的平方,那么这个三角形是直角三角形 吗? 例1.根据下列条件,分别判断以a,b,c 为边的三角形是不是直角三角形? (1)a=7,b=24,c=25; (2)a= , b=1,c= . 3 2 3 2 练习一 n 下面以a,b,c为边长的三角形是不是直角三 角形?如果是那么哪一个角是直角? (1) a=25 b=20 c=15 ________ ________ (3) a=41 b=9 c=40 _______ ________ (4) a:b: c=3:4:5 ________ ________ 是 是 是 是 ∠ A=900 ∠ B=900 ∠ A=900 ∠ C=900 (2) a=1 b=2 c= ________ ________3 例2 如果△ABC的三边长分别为 a,b,c,且 a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数) 则△ABC是直角三角形 解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数) ∴a2+b2=(m2-n2)2+(2mn)2 =m4-2m2n2+n4+4m2n2 =m4+2m2n2+n4 =(m2+n2)2 =c2 ∴△ABC是直角三角形。 课堂练习: 一判断题. 1.ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在 ABC中, C=90°,若AC=6,CB=8,则ABC面积 为_____,斜边为上的高为______. 例1 n 已知:在△ ABC中, AB=15cm, AC=20cm, BC=25cm,AD是BC边上的 中线。求: AD的长。 D C A B CB = 2.53 cm AC = 2.01 cm BA = 1.53 cm 解: ∵ AB=15cm,AC=20cm,BC=25cm ∴ AB2+AC2=225+400=625 BC2=625 ∴ AB2+AC2=BC2 ∵ ∠ BAC=900(勾股定理的逆定理) ∴ AD= BC= cm (直角三角形斜边上的中线等于 斜边的一半) 2 1 2 25 ∵ S △ ABC= AC • AB = BC•AE 2 1 2 1 ∴ AD= 12 25 1520 BC ABAC n 已知:在△ ABC中, AB=15cm, AC=20cm, BC=25cm,AD是BC边上的高。 求: AD的长。 练习 中 线。求: AD的长。 D C A B CB = 2.53 cm AC = 2.01 cm BA = 1.53 cm D B AC BC = 2.50 cm BA = 1.48 cm CA = 2.01 cm 解: ∵ AB=15cm,AC=20cm,BC=25cm ∴ AB2+AC2=225+400=625 BC2=625 ∴ AB2+AC2=BC2 ∵ ∠ BAC=900(勾股定理的逆定理) 如图:边长为4的正方形ABCD中,F是DC的中 点,且CE= BC,则AF⊥EF,试说明理由 4 1 A B D C F E 解:连接AE ∵ABCD是正方形,边长是4,F是 DC的中点,EC=1/4BC ∴根据勾股定理,在 Rt△ADF,AF2=AD2+DF2=20 Rt△EFC,EF2=EC2+FC2=5 Rt△ABE,AE2=AB2+BE2=25 ∴AD=4,DF=2,FC=2,EC=1 ∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF 求:(1) S四边形ABCD。 32CD= cm, AD=2cm, AC⊥AB。 已知:在四边形ABCD中,AB=3cm, BC=5cm,例2 D CB A DC = 3.52 cm AD = 2.03 cm BC = 5.08 cm CA = 4.11 cm AB = 3.00 cm ∵AC⊥AB(已知) ∴ AC2+AB2=BC2(勾股定理) ∵ AB=3cm,BC=5cm cmABBCAC 435 2222 又∵CD=2 cm AD=2cm(已知)3 ∴ AC2=16 , CD2+AD2=12+4=16 ∴ AC2=CD2+AD2 ∴ ∠ADC=900(勾股定理的逆定理 ∴ S四边形ABCD=S △ ABC+ S△ ACD ∴ = ×3 × 4+ × 2•2 =6+2 (cm2) = AB •AC+ AD •CD 2 1 2 1 3 3 2 1 2 1 解: 解:∵ RtADC中AD=2, AC=4 ∴ ∠ DCA=300(在直 角三角形中如果一条直 角边等于斜边的一半, 那么这条直角边所对的 角等于300) ∴ AD= AC2 1 求:(1) S四边形ABCD。(2)∠ DCA的度数 32CD= cm, AD=2cm, AC⊥AB。 已知:在四边形ABCD中,AB=3cm, BC=5cm,例2 D CB A DC = 3.52 cm AD = 2.03 cm BC = 5.08 cm CA = 4.11 cm AB = 3.00 cm 小结 n 利用勾股定理,已知直角三角形的两条边,可 以求出第三边,利用勾股定理的逆定理,可以 判定一个角为直角。从而判定直角三角形,也 可以用来判定两 直线互相垂直。 思考题 n 在平面直角坐标系中有RT △ ABC,已知A(2, 4),B(0,-2),点A(2,4),B(0,- 2),点C在X轴上,求点C的坐标。查看更多