- 2021-05-08 发布 |
- 37.5 KB |
- 10页


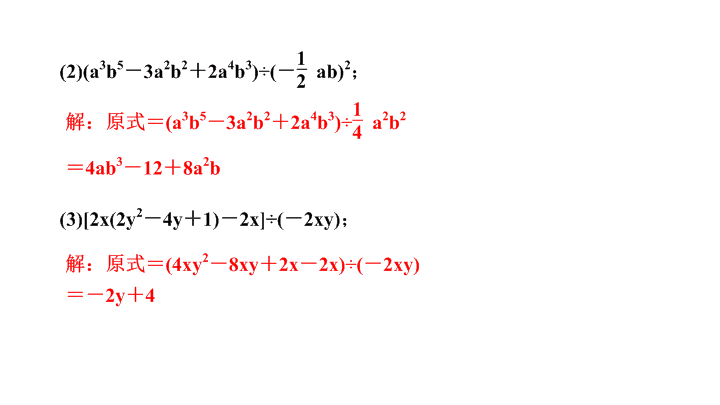
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级数学上册专题训练(十)PPT
第十四章 整式的乘法与因式分解 人教版 专题训练(十) 整式的化简求值及应用 类型一 整式的化简 1 .计算: (1)( - 3x 2 y) 2 · (6xy 3 )÷(9x 3 y 4 ) ; 解:原式= 9x 4 y 2 · 6xy 3 ÷9x 3 y 4 = 54x 5 y 5 ÷9x 3 y 4 = 6x 2 y 类型二 整式的化简求值 2 .先化简,再求值: (1)(a - 2)a - (a + 6)(a - 2) ,其中 a =- 2 ; 解:原式= a 2 - 2a - a 2 - 4a + 12 =- 6a + 12. 当 a =- 2 时,原式= 12 + 12 = 24 (3)3(x - 1)(x + 3) - 2(x - 5)(x - 2) ,其中 x 满足 x 2 + 20x + 1 = 0. 解:原式= 3(x 2 + 2x - 3) - 2(x 2 - 7x + 10) = 3x 2 + 6x - 9 - 2x 2 + 14x - 20 = x 2 + 20x - 29. ∵x 2 + 20x + 1 = 0 ,∴ x 2 + 20x =- 1. ∴ 原式=- 1 - 29 =- 30 类型三 用待定系数法求字母的值 3 .已知 (x 2 + mx + 3)(x 2 - 3x + n) 的展开式中不含 x 2 项和 x 3 项,求 m , n 的值. 解:原式= x 4 - 3x 3 + nx 2 + mx 3 - 3mx 2 + mnx + 3x 2 - 9x + 3n = x 4 - 3x 3 + mx 3 + nx 2 - 3mx 2 + 3x 2 + mnx - 9x + 3n = x 4 + (m - 3)x 3 + (n - 3m + 3)x 2 + mnx - 9x + 3n. 由于展开式中不含 x 2 项和 x 3 项, ∴ m - 3 = 0 且 n - 3m + 3 = 0 , ∴解得 m = 3 , n = 6 4 .一位同学在研究多项式除法时,把被除式的二次项系数写成 a ,而把结果的一次项系数又写成了- b ,等式如下: (x 3 + ax 2 + 1)÷(x + 1) = x 2 - bx + 1 ,现请你帮他求出 a , b 的值. 解:∵ x 3 + ax 2 + 1 = (x + 1) · (x 2 - bx + 1) = x 3 + (1 - b) · x 2 + (1 - b) · x + 1 , ∴ a = 1 - b , 1 - b = 0 解得 a = 0 , b = 1 类型四 利用整式的乘除运算探索数式规律 5 . (1) 计算: (x + 1)(x 2 - x + 1) = ____________ ; (m + 2)(m 2 - 2m + 4) = _________ ; (2a + 1)(4a 2 - 2a + 1) = __________ . (2) 观察上面运算结果,你发现了什么规律?请你用含有字母 a , b 的式子表示这个规律,并加以证明. 解: (2) 规律: (a + b)(a 2 - ab + b 2 ) = a 3 + b 3 . 证明: (a + b)(a 2 - ab + b 2 ) = a 3 - a 2 b + ab 2 + a 2 b - ab 2 + b 3 = a 3 + b 3 x 3 + 1 m 3 + 8 8a 3 + 1查看更多