- 2021-05-08 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年甘肃省张掖市高考数学一模试卷(文科)
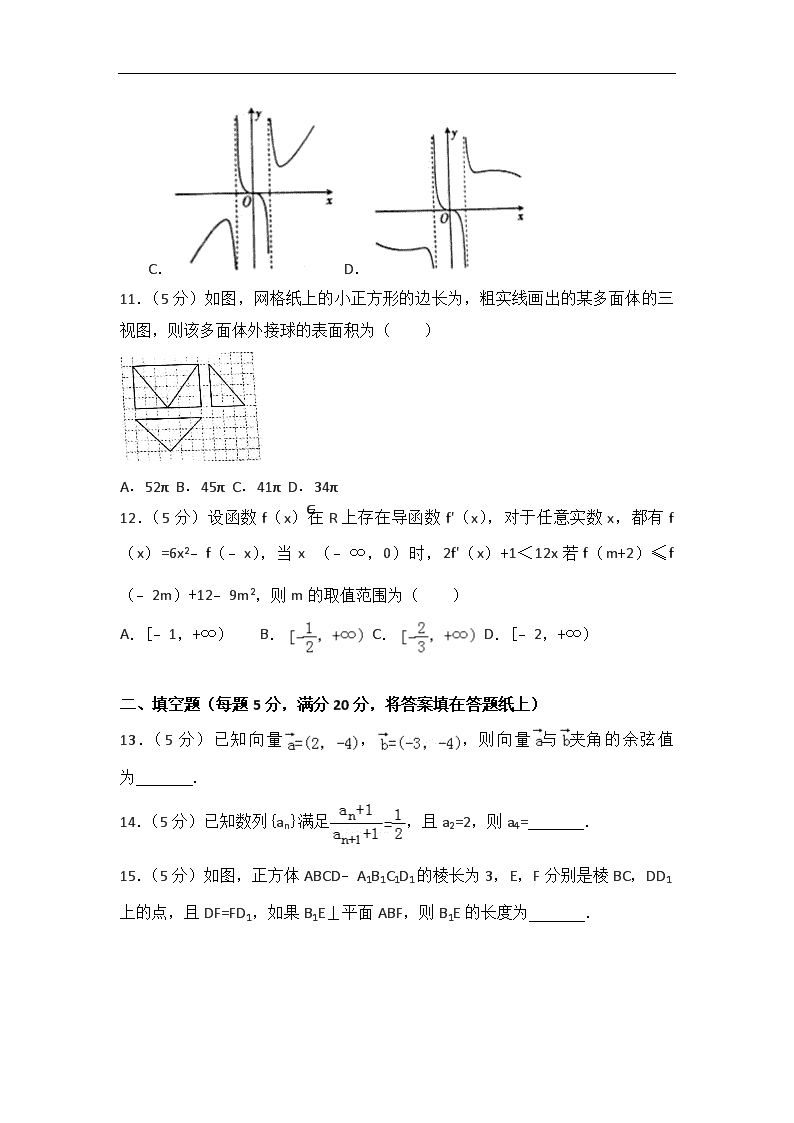
2018年甘肃省张掖市高考数学一模试卷(文科) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)若集合,则A∩B=( ) A.(4,9) B.(9,+∞) C.(10,+∞) D.(9,10) 2.(5分)若复数z=5+3i,且iz=a+bi(a,b∈R)则a+b=( ) A.2 B.﹣2 C.﹣8 D.8 3.(5分)如表是我国某城市在2017年1月份至10月份各月最低温与最高温(°C)的数据一览表. 月份 1 2 3 4 5 6 7 8 9 10 最高温 5 9 9 11 17 24 27 30 31 21 最低温 ﹣12 ﹣3 1 ﹣2 7 17 19 23 25 10 已知该城市的各月最低温与最高温具有相关关系,根据该一览表,则下列结论错误的是( ) A.最低温与最高温为正相关 B.每月最高温与最低温的平均值在前8个月逐月增加 C.月温差(最高温减最低温)的最大值出现在1月 D.1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大 4.(5分)设等差数列{an}的公差为d,且a1a2=35,2a4﹣a6=7,则d=( ) A.4 B.3 C.2 D.1 5.(5分)若是第二象限角,则=( ) A. B.5 C. D.10 6.(5分)已知双曲线的实轴长为8,则该双曲线的渐近线的斜率为( ) A. B. C. D. 7.(5分)若实数x,y满足约束条件,则z=4x﹣y的最大值为( ) A.3 B.﹣1 C.﹣4 D.12 8.(5分)如图所示的程序框图,运行程序后,输出的结果等于( ) A.2 B.3 C.4 D.5 9.(5分)已知函数的最小正周期为6π,且取图象向右平移个单位后得到函数g(x)=sinwx的图象,则φ=( ) A. B. C. D. 10.(5分)f(x)=的部分图象大致是( ) A. B. C. D. 11.(5分)如图,网格纸上的小正方形的边长为,粗实线画出的某多面体的三视图,则该多面体外接球的表面积为( ) A.52π B.45π C.41π D.34π 12.(5分)设函数f(x)在R上存在导函数f'(x),对于任意实数x,都有f(x)=6x2﹣f(﹣x),当x∈(﹣∞,0)时,2f'(x)+1<12x若f(m+2)≤f(﹣2m)+12﹣9m2,则m的取值范围为( ) A.[﹣1,+∞) B. C. D.[﹣2,+∞) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.(5分)已知向量,,则向量与夹角的余弦值为 . 14.(5分)已知数列{an}满足,且a2=2,则a4= . 15.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为3,E,F分别是棱BC,DD1上的点,且DF=FD1,如果B1E⊥平面ABF,则B1E的长度为 . 16.(5分)已知抛物线y2=2x,A,B是抛物线上的两点,线段AB的垂直平分线与x轴相交于点P(x00),则x0的取值范围是 .(用区间表示) 三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=4,,bsinC=2sinB. (1)求b的值; (2)求△ABC的面积. 18.(12分)共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在[60,80),[20,40),[40,60)三组对应的人数依次成等差数列 (1)求频率分布直方图中a,b的值. (2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率. 19.(12分)如图,四边形ABCD是矩形AB=3,PE⊥ 平面ABCD,PE=. (1)证明:平面PAC⊥平面PBE; (2)设AC与BE相交于点F,点G在棱PB上,且CG⊥PB,求三棱锥F﹣BCG的体积. 20.(12分)已知椭圆的左右焦点分别为F1,F2,上顶点为M,若直线MF1的斜率为1,且与椭圆的另一个交点为N,△F2MN的周长为. (1)求椭圆的标准方程; (2)过点F1的直线l(直线l的斜率不为1)与椭圆交于P,Q两点,点P在点Q的上方,若,求直线l的斜率. 21.(12分)已知函数f(x)=2(x﹣1)ex. (1)若函数f(x)在区间(a,+∞)上单调递增,求f(a)的取值范围; (2)设函数g(x)=ex﹣x+p,若存在x0∈[1,e],使不等式g(x0)≥f(x0)﹣x0成立,求p的取值范围. 22.(10分)已知曲线C1的极坐标方程为ρ2cos2θ=8,曲线C2的极坐标方程为,曲线C1、C2相交于A、B两点.(p∈R) (Ⅰ)求A、B两点的极坐标; (Ⅱ)曲线C1与直线(t为参数)分别相交于M,N两点,求线段MN的长度. 23.已知函数f(x)=|x﹣a|﹣|x+3|,a∈R. (1)当a=﹣1时,解不等式f(x)≤1; (2)若x∈[0,3]时,f(x)≤4,求a的取值范围. 2018年甘肃省张掖市高考数学一模试卷(文科) 参考答案与试题解析 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)若集合,则A∩B=( ) A.(4,9) B.(9,+∞) C.(10,+∞) D.(9,10) 【解答】解:A={x|x>9},B={x|4<x<10}, 则A∩B={x|9<x<10}=(9,10), 故选:D. 2.(5分)若复数z=5+3i,且iz=a+bi(a,b∈R)则a+b=( ) A.2 B.﹣2 C.﹣8 D.8 【解答】解:复数z=5+3i,且iz=a+bi(a,b∈R), 可得﹣3+5i=a+bi,. 解得a=﹣3,b=5, ∴a+b=2. 故选:A. 3.(5分)如表是我国某城市在2017年1月份至10月份各月最低温与最高温(°C)的数据一览表. 月份 1 2 3 4 5 6 7 8 9 10 最高温 5 9 9 11 17 24 27 30 31 21 最低温 ﹣12 ﹣3 1 ﹣2 7 17 19 23 25 10 已知该城市的各月最低温与最高温具有相关关系,根据该一览表,则下列结论错误的是( ) A.最低温与最高温为正相关 B.每月最高温与最低温的平均值在前8个月逐月增加 C.月温差(最高温减最低温)的最大值出现在1月 D.1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大 【解答】解:根据题意,依次分析选项: 对于A,知该城市的各月最低温与最高温具有相关关系,由数据分析可得最低温与最高温为正相关,则A正确; 对于B,由表中数据,每月最高温与最低温的平均值依次为:﹣3.5,3,5,4.5,12,20.5,23,26.5,28,15.5,在前8个月不是逐月增加,则B错误; 对于C,由表中数据,月温差依次为:17,12,8,13,10,7,8,7,6,11;月温差的最大值出现在1月,C正确; 对于D,有C的结论,分析可得1月至4月的月温差相对于7月至10月,波动性更大,D正确; 故选:B. 4.(5分)设等差数列{an}的公差为d,且a1a2=35,2a4﹣a6=7,则d=( ) A.4 B.3 C.2 D.1 【解答】解:∵等差数列{an}的公差为d,且a1a2=35,2a4﹣a6=7, ∴, 解得a1=5,d=2. 故选:C. 5.(5分)若是第二象限角,则=( ) A. B.5 C. D.10 【解答】解:∵是第二象限角, ∴tanα=﹣,可得:cosα=﹣=﹣, ∴====10. 故选:D. 6.(5分)已知双曲线的实轴长为8,则该双曲线的渐近线的斜率为( ) A. B. C. D. 【解答】解:双曲线的实轴长为8, 可得:m2+12=16,解得m=2,m=﹣2(舍去). 所以,双曲线的渐近线方程为:. 则该双曲线的渐近线的斜率:. 故选:C. 7.(5分)若实数x,y满足约束条件,则z=4x﹣y的最大值为( ) A.3 B.﹣1 C.﹣4 D.12 【解答】解:实数x,y满足约束条件, 表示的平面区域如图所示, 当直线z=4x﹣y过点A时,目标函数取得最大值, 由解得A(3,0), 在y轴上截距最小,此时z取得最大值:12. 故选:D. 8.(5分)如图所示的程序框图,运行程序后,输出的结果等于( ) A.2 B.3 C.4 D.5 【解答】解:模拟程序的运行,可得: a=2,s=0,n=1, s=2,a=, 满足条件s<3,执行循环体,n=2,s=2+=,a=, 满足条件s<3,执行循环体,n=3,s=+=,a=, 此时,不满足条件s<3,退出循环,输出n的值为3. 故选:B. 9.(5分)已知函数的最小正周期为6π,且取图象向右平移个单位后得到函数g(x)=sinwx的图象,则φ=( ) A. B. C. D. 【解答】解:∵函数的最小正周期为6π, ∴=6π,则ω=, 则f(x)=sin(x+φ),图象向右平移个单位后得到y=sin[(x﹣)+φ]=sin(x﹣+φ)=sinx, 此时﹣+φ=2kπ,得φ=+2kπ, ∵|φ|<,∴φ=, 故选:A 10.(5分)f(x)=的部分图象大致是( ) A. B. C. D. 【解答】解:∵f(﹣x)=f(x)∴函数f(x)为奇函数,排除A, ∵x∈(0,1)时,x>sinx,x2+x﹣2<0,故f(x)<0,故排除B; 当x→+∞时,f(x)→0,故排除C; 故选:D 11.(5分)如图,网格纸上的小正方形的边长为,粗实线画出的某多面体的三视图,则该多面体外接球的表面积为( ) A.52π B.45π C.41π D.34π 【解答】解:由三视图可知:该几何体为一个四棱锥,底面ABCD是矩形,其中AB=4,AD=6,侧面PBC⊥底面垂ABCD. 设AC∩BD=O,则OA=OB=OC=OD=,OP=, ∴O该多面体外接球的球心,半径R=,∴该多面体外接球的表面积为S=4πR2=52π. 故选:A 12.(5分)设函数f(x)在R上存在导函数f'(x),对于任意实数x,都有f(x)=6x2﹣f(﹣x),当x∈(﹣∞,0)时,2f'(x)+1<12x若f(m+2)≤f(﹣2m)+12﹣9m2,则m的取值范围为( ) A.[﹣1,+∞) B. C. D.[﹣2,+∞) 【解答】解:∵f(x)﹣3x2+f(﹣x)﹣3x2=0, 设g(x)=f(x)﹣3x2, 则g(x)+g(﹣x)=0, ∴g(x)为奇函数, 又g′(x)=f′(x)﹣6x<﹣, ∴g(x)在x∈(﹣∞,0)上是减函数,从而在R上是减函数, 又f(m+2)≤f(﹣2m)+12m+12﹣9m2 等价于f(m+2)﹣3(m+2)2≤f(﹣2m)﹣3(﹣2m)2, 即g(m+2)≤g(﹣2m), ∴m+2≥﹣2m, 解可得:m≥﹣; 故选:C. 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.(5分)已知向量,,则向量与夹角的余弦值为 . 【解答】解:根据题意,设向量与夹角为θ, 向量,, 则||=2,||=5,且•=2×(﹣3)+(﹣4)×(﹣4)=10, cosθ===, 故答案为:. 14.(5分)已知数列{an}满足,且a2=2,则a4= 11 . 【解答】解:∵, ∴=2 ∴{an+1}是公比q=2的等比数列, 则=22=4, 即=4,则a4+1=3×4=12, 则a4=11, 故答案为:11. 15.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为3,E,F分别是棱BC,DD1上的点,且DF=FD1,如果B1E⊥平面ABF,则B1E的长度为 . 【解答】解:以D为坐标原点,DC,DA,DD1所在直线为x,y,z轴, 建立空间直角坐标系, 可得A(0,3,0),B(3,3,0),F(0,0,),B1(3,3,3), E(3,t,0), 则=(0,t﹣3,﹣3),=(3,0,0),=(﹣3,﹣3,), B1E⊥平面ABF, 可得B1E⊥AB,B1E⊥BF, 即•=0,•=0, 即有0×3+(t﹣3)×0+﹣3×0=0, 0×(﹣3)+(t﹣3)×(﹣3)+(﹣3)×=0, 解得t=, 则=(0,﹣,﹣3), 可得B1E的长度为=. 故答案为:. 16.(5分)已知抛物线y2=2x,A,B是抛物线上的两点,线段AB的垂直平分线与x轴相交于点P(x00),则x0的取值范围是 (1,+∞) .(用区间表示) 【解答】解:设A(x1,y1),B(x2,y2),AB中点M. 直线AB的方程为y=kx+m,(k≠0) 得ky2﹣2y+2m=0 , △=4﹣8km>0⇒km< xM═,yM= ⇒直线PM的方程为y﹣=﹣ 令y=0,得x0= ∵ ∴x0=>1 故答案为:(1,+∞) 三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=4,,bsinC=2sinB. (1)求b的值; (2)求△ABC的面积. 【解答】解:(1)∵bsinC=2sinB, ∴由正弦定理得:bc=2b,即c=2, 由余弦定理得. ∴; (2)∵a=4,c=2,. ∴. 18.(12分)共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在[60,80),[20,40),[40,60)三组对应的人数依次成等差数列 (1)求频率分布直方图中a,b的值. (2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率. 【解答】解:(1)由(0.0025×2+0.0075+3a)×20=1 解得a=0.0125, 又b+0.0165=2a=0.0025,∴b=0.0085. (2)“忠实用户”“潜力用户”的人数之比为:(0.0075+0.0025):(0.0125+0.0025)=2:3, 所以“忠实用户”抽取人, “潜力用户”抽取人, 记事件:从5人中任取3人恰有1人为“忠实用户” 设两名“忠实用户”的人记为:B1,B2,三名“潜力用户”的人记为:b1,b2,b3, 则这5人中任选3人有: (B1,B2,b1),(B1,B2,b2),(B1,B2,b3),(B1,b1,b2),(B1,b1,b3)(B1,b2,b3), (B2,b1,b2),(B2,b1,b3),(B1,b2,b3),(b1,b2,b3),共10种情形, 符合题设条件有: (B1,b1,b2),(B1,b1,b3),(B1,b2,b3),(B2,b1,b2),(B2,b1,b3),(B1,b2,b3)共有6种, 因此恰好1人为“忠实用户”的概率为. 19.(12分)如图,四边形ABCD是矩形AB=3,PE⊥平面ABCD,PE=. (1)证明:平面PAC⊥平面PBE; (2)设AC与BE相交于点F,点G在棱PB上,且CG⊥PB,求三棱锥F﹣BCG的体积. 【解答】证明:(1)因为四边形ABCD是矩形,, 所以, 又, 所以△ABC~△BCE,∠BCE=∠ACB, 因为, 所以AC⊥BE, 又PE⊥平面ABCD,所以AC⊥PE, 又面PE∩BE=E,所以AC⊥平面PBE. (2)因为,所以, 又BC=3,CG⊥PB, 所以G为棱PB的中点,G到平面ABC的距离等于, 由(1)知△ABF~△CEF,所以, 所以, 所以. 20.(12分)已知椭圆的左右焦点分别为F1,F2,上顶点为M,若直线MF1的斜率为1,且与椭圆的另一个交点为N,△F2MN的周长为. (1)求椭圆的标准方程; (2)过点F1的直线l(直线l的斜率不为1)与椭圆交于P,Q两点,点P在点Q的上方,若,求直线l的斜率. 【解答】解:(1)根据题意,因为△F1MN的周长为,所以,即, 由直线MF1的斜率1,得, 因为a2=b2+c2,所以b=1,c=1, 所以椭圆的标准方程为. (2)由题意可得直线MF1方程为y=x+1,联立得,解得N(﹣,﹣), 所以, 因为,即, 所以|QF1|=2|PF1|, 当直线l的斜率为0时,不符合题意, 故设直线l的方程为x=my﹣1,P(x1,y1),Q(x2,y2), 由点P在点Q的上方,且|y2|=|2y1|, 则有y2=﹣2y1, 联立,所以(m2+2)y2﹣2my﹣1=0,所以, 消去y2得,所以,得, 又由画图可知不符合题意,所以, 故直线l的斜率为. 21.(12分)已知函数f(x)=2(x﹣1)ex. (1)若函数f(x)在区间(a,+∞)上单调递增,求f(a)的取值范围; (2)设函数g(x)=ex﹣x+p,若存在x0∈[1,e],使不等式g(x0)≥f(x0)﹣x0成立,求p的取值范围. 【解答】解:(1)由f'(x)=2xex>0,得x>0, 所以f(x)在(0,+∞)上单调递增,所以a≥0,所以f(a)≥f(0)=﹣2, 所以f(a)的取值范围是[﹣2,+∞). (2)因为存在x0∈[1,e],使不等式成立, 所以存在x0∈[1,e],使成立, 令h(x)=(2x﹣e)ex,从而p≥h(x)min,h'(x)=(2x﹣1)ex, 因为x≥1,所以2x﹣1≥1,ex>0,所以h'(x)>0, 所以h(x)=(2x﹣e)ex在[1,e]上单调递增, 所以h(x)min=h(1)=﹣e,所以p≥﹣e, 实数p的取值范围是[﹣e,+∞). 22.(10分)已知曲线C1的极坐标方程为ρ2cos2θ=8,曲线C2的极坐标方程为,曲线C1、C2相交于A、B两点.(p∈R) (Ⅰ)求A、B两点的极坐标; (Ⅱ)曲线C1与直线(t为参数)分别相交于M,N两点,求线段MN的长度. 【解答】解:(Ⅰ)由得:, ∴ρ2=16, 即ρ=±4. ∴A、B两点的极坐标为:或. (Ⅱ)由曲线C1的极坐标方程ρ2cos2θ=8化为ρ2(cos2θ﹣sin2θ)=8, 得到普通方程为x2﹣y2=8. 将直线代入x2﹣y2=8, 整理得. ∴|MN|==. 23.已知函数f(x)=|x﹣a|﹣|x+3|,a∈R. (1)当a=﹣1时,解不等式f(x)≤1; (2)若x∈[0,3]时,f(x)≤4,求a的取值范围. 【解答】解:(1)当a=﹣1时,不等式为|x+1|﹣|x+3|≤1; 当x≤﹣3时,不等式转化为﹣(x+1)+(x+3)≤1,不等式解集为空集; 当﹣3<x<﹣1时,不等式转化为﹣(x+1)﹣(x+3)≤1,解之得; 当x≥﹣1时,不等式转化为(x+1)﹣(x+3)≤1,恒成立; 综上所求不等式的解集为. (2)若x∈[0,3]时,f(x)≤4恒成立,即|x﹣a|≤x+7,亦即﹣7≤a≤2x+7恒成立, 又因为x∈[0,3],所以﹣7≤a≤7, 所以a的取值范围为[﹣7,7]. 查看更多