高考小题标准练十理新人教版
高考小题标准练(十)
满分 80 分,实战模拟,40 分钟拿下高考客观题满分!
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.)
1.已知集合 A={x|lg(x+1)≤0},集合 B={x|2x≤1},则 A∩B=( )
A.{x|-1
1)
所以 f(20)=2·202-39=761.
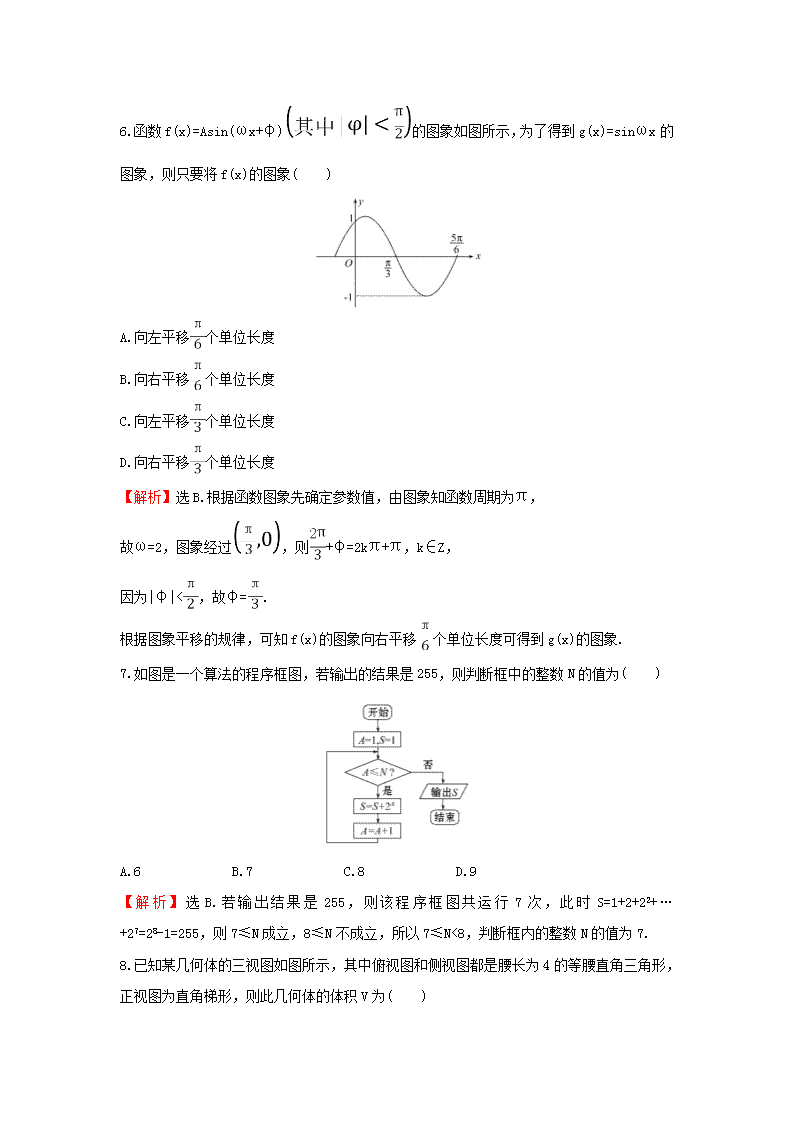
6.函数 f(x)=Asin(ωx+φ) 的图象如图所示,为了得到 g(x)=sinωx 的
图象,则只要将 f(x)的图象( )
A.向左平移 个单位长度
B.向右平移 个单位长度
C.向左平移 个单位长度
D.向右平移 个单位长度
【解析】选 B.根据函数图象先确定参数值,由图象知函数周期为π,
故ω=2,图象经过 ,则 +φ=2kπ+π,k∈Z,
因为|φ|< ,故φ= .
根据图象平移的规律,可知 f(x)的图象向右平移 个单位长度可得到 g(x)的图象.
7.如图是一个算法的程序框图,若输出的结果是 255,则判断框中的整数 N 的值为( )
A.6 B.7 C.8 D.9
【解析】选 B.若输出结果是 255,则该程序框图共运行 7 次,此时 S=1+2+22+…+27=28-1=255,
则 7≤N 成立,8≤N 不成立,所以 7≤N<8,判断框内的整数 N 的值为 7.
8.已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为 4 的等腰直角三角形,
正视图为直角梯形,则此几何体的体积 V 为( )
A. B. C. D.40
【解析】选 B.观察三视图可知,该几何体为四棱锥,底面为直角梯形,两个侧面与底面垂
直,棱锥的高为 4,由图中数据得该几何体的体积为 × ×4×4= .
9.在△ABC 中, · =0,AB=2,AC=1,E,F 为 BC 的三等分点,则 · =( )
A. B. C. D.
【解析】选 B.由 · =0,
又因为 AB 和 AC 为三角形的两条边,不可能为 0,
所以 与 垂直,
所以△ABC 为直角三角形.
以 AC 为 x 轴,以 AB 为 y 轴建立平面直角坐标系,如图所示,
则 A(0,0),B(0,2),C(1,0),
由 E,F 为 BC 的三等分点知 E ,F ,
所以 = , = ,
所以 · = × + × = .
10.已知函数 f(x)=lnx-ax2+ax 恰有两个零点,则实数 a 的取值范围为( )
A.(-∞,0) B.(0,+∞)
C.(0,1)∪(1,+∞) D.(-∞,0)∪{1}
【解析】选 C.函数 f(x)的定义域为(0,+∞),
由题知方程 lnx-ax2+ax=0,
即方程 =a(x-1)恰有两解,
设 g(x)= ,则 g′(x)= ,
当 00,
当 x>e 时,g′(x)<0,
所以 g(x)在(0,e)上是增函数,在(e,+∞)上是减函数,且 g(1)=0,
当 x>e 时,g(x)>0,g′(1)=1.
作出函数 y=g(x)与函数 y=a(x-1)的图象如图所示,
由图可知,函数 y=g(x)的图象与函数 y=a(x-1)的图象恰有 2 个交点的充要条件为 01.
11.已知 x,y 满足约束条件 则下列目标函数中,在点(3,1)处取得最小值的
是( )
A.z=2x-y B.z=-2x+y
C.z=- x-y D.z=2x+y
【解析】选 B.作出不等式组表示的平面区域如图所示.
A,由 z=2x-y 得 y=2x-z,平移直线可得当直线经过点 A(3,1)时,截距最小,此时 z 最大;
B,由 z=-2x+y 得 y=2x+z,平移直线可得当直线经过点 A(3,1)时,截距最小,此时 z 最小,
符合题意;
C,由 z=- x-y 得 y=- x-z,平移直线可得当直线经过点 B 时,截距最大,此时 z 最小;
D,由 z=2x+y 得 y=-2x-z,平移直线可得当直线经过点 A(3,1)时,截距最大,此时 z 最大,
不符合题意.
12.已知 F 为抛物线 y2=x 的焦点,点 A,B 在该抛物线上且位于 x 轴的两侧, · =2(其
中 O 为坐标原点),则△ABO 与△AFO 面积之和的最小值是( )
A.2 B.3 C. D.
【解析】选 B.设直线 AB 的方程为 x=ny+m(如图),
A(x1,y1),B(x2,y2),
因为 · =2,所以 x1x2+y1y2=2.
又 =x1, =x2,所以 y1y2=-2.
联立 得 y2-ny-m=0,
所以 y1y2=-m=-2,所以 m=2,即点 M(2,0).
又 S△ABO=S△AMO+S△BMO
= |OM||y1|+ |OM||y2|=y1-y2,
S△AFO= |OF|·|y1|= y1,
所以 S△ABO+S△AFO=y1-y2+ y1
= y1+ ≥2 =3,
当且仅当 y1= 时,等号成立.
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分.请把正确答案填在题中横线上)
13.设 a= 2xdx,则 的展开式中常数项为________.
【 解 析 】 因 为 a= 2xdx=x2 =3 , 故 二 项 式 展 开 式 的 通 项 公 式 为
Tr+1= (3x)6-r(-1)rx-r= 36-r(-1)rx6-2r , 令 6-2r=0 , 解 得 r=3 , 故 所 求 常 数 项 为
·33·(-1)3=-540.
答案:-540
14.已知数列{an}满足 a1=1,an+1·an=2n(n∈N*),则 S2016=________.
【解析】由 an+1·an=2n 可知,an+2·an+1=2n+1,
得 =2,因此 a1,a3,a5…构成一个以 1 为首项,2 为公比的等比数列,因此 a2,a4,a6…
构成一个以 2 为首项,2 为公比的等比数列,
从而 S2016=(a1+a3+…+a2015)+(a2+a4+…+a2016)= +2× =3(21008-1).
答案:3(21008-1)
15.若△ΑΒC 的内角Α,Β满足 =2cos ,则当Β取最大值时,角 C 的大小
为________.
【解析】由 =2cos(A+B)可得 sinB=-2sinAcosC,
3sinAcosC=-cosAsinC,得 tanC=-3tanA,
所以 tanB=-tan(A+C)=- = ≤ = .
当且仅当 tanA= ,即 tanC=- 时取等号,
因此当 B 取最大值时,角 C= .
答案:
16.已知函数 f(x)=(x2-1)(x2+ax+b)的图象关于直线 x=3 对称,则函数 f(x)的值域为
________.
【解析】由题知 f(-1)=0,f(1)=0,
因为函数 f(x)的图象关于直线 x=3 对称,
所以 f(7)=f(-1)=0 且 f(5)=f(1)=0,
即 解得 a=-12,b=35,
所以 f(x)=(x2-1)(x2-12x+35)
=(x+1)(x-1)(x-5)(x-7)
=(x2-6x+5)(x2-6x-7),
设 t=x2-6x-1(t≥-10),
则 f(t)=(t+6)(t-6)(t≥-10)=t2-36≥-36,
故函数的值域为[-36,+∞).
答案: